pytorch中常用的损失函数

1 损失函数的作用

损失函数是模型训练的基础，并且在大多数机器学习项目中，如果没有损失函数，就无法驱动模型做出正确的预测。通俗地说，损失函数是一种数学函数或表达式，用于衡量模型在某些数据集上的表现。损失函数在深度学习主要作用如下：

衡量模型性能：损失函数用于评估模型的预测结果与真实结果之间的误差程度。较小的损失值表示模型的预测结果与真实结果更接近，反之则表示误差较大。因此，损失函数提供了一种度量模型性能的方式。
参数优化：在训练机器学习和深度学习模型时，损失函数被用作优化算法的目标函数。通过最小化损失函数，可以调整模型的参数，使模型能够更好地逼近真实结果。
反向传播：在深度学习中，通过反向传播算法计算损失函数对模型参数的梯度。这些梯度被用于参数更新，以便优化模型。损失函数在反向传播中扮演着重要的角色，指导参数的调整方向。
防止过拟合：过拟合是指模型在训练数据上表现良好，但在新数据上表现较差的现象。损失函数可以帮助在训练过程中监控模型的过拟合情况。通过观察训练集和验证集上的损失，可以及早发现模型是否过拟合，从而采取相应的措施，如正则化等。

2 pytorch中常见的损失函数

损失函数	名称	适用场景
torch.nn.MSELoss()	均方误差损失	回归
torch.nn.L1Loss()	平均绝对值误差损失	回归
torch.nn.CrossEntropyLoss()	交叉熵损失	多分类
torch.nn.NLLLoss()	负对数似然函数损失	多分类
torch.nn.NLLLoss2d()	图片负对数似然函数损失	图像分割
torch.nn.KLDivLoss()	KL散度损失	回归
torch.nn.BCELoss()	二分类交叉熵损失	二分类
torch.nn.MarginRankingLoss()	评价相似度的损失
torch.nn.MultiLabelMarginLoss()	多标签分类的损失	多标签分类
torch.nn.SmoothL1Loss()	平滑的L1损失	回归
torch.nn.SoftMarginLoss()	多标签二分类问题的损失	多标签二分类

2.1 L1损失函数

预测值与标签值进行相差，然后取绝对值，根据实际应用场所，可以设置是否求和，求平均，公式可见下，Pytorch调用函数：nn.L1Loss

import torch
import torch.nn as nnLoss_fn = nn.L1Loss(size_average=None, reduce=None, reduction='mean')input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
output = Loss_fn(input, target)
print(output)

运行结果显示如下：

tensor(1.4177, grad_fn=<MeanBackward0>)

2.2 L2损失函数

预测值与标签值进行相差，然后取平方，根据实际应用场所，可以设置是否求和，求平均，公式可见下，Pytorch调用函数：nn.MSELoss

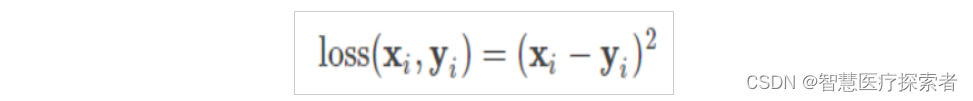
import torch.nn as nn
import torchloss = nn.MSELoss(size_average=None, reduce=None, reduction='mean')input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
output = loss(input, target)
print(output)

运行结果显示如下：

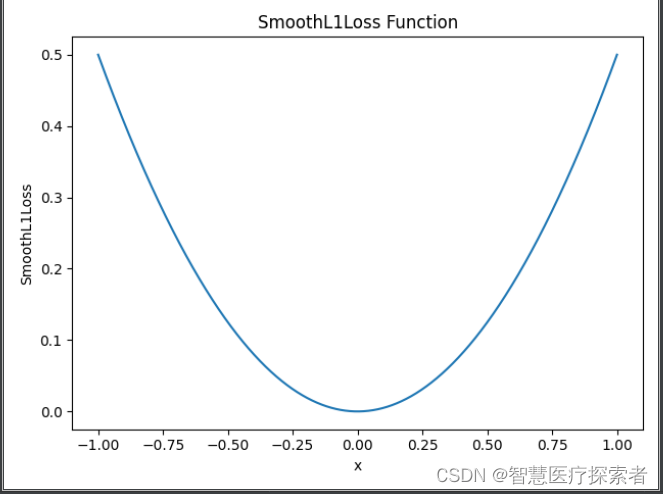
tensor(1.7956, grad_fn=<MseLossBackward0>)

2.3 Huber Loss损失函数

简单来说就是L1和L2损失函数的综合版本，结合了两者的优点，公式可见下，Pytorch调用函数：nn.SmoothL1Loss

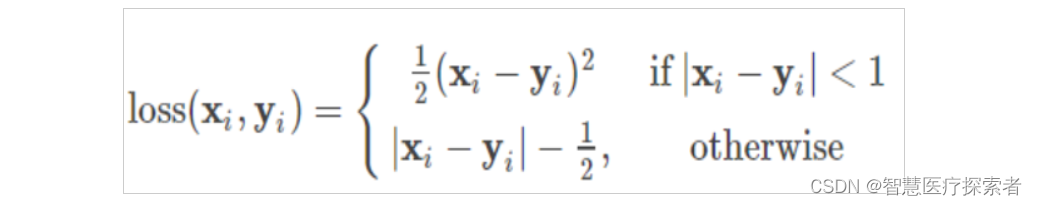
import matplotlib.pyplot as plt
import torch# 定义函数和参数
smooth_l1_loss = nn.SmoothL1Loss(reduction='none')
x = torch.linspace(-1, 1, 10000)
y = smooth_l1_loss(torch.zeros(10000), x)# 绘制图像
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('SmoothL1Loss')
plt.title('SmoothL1Loss Function')
plt.show()

运行结果显示如下：

2.4 二分类交叉熵损失函数

简单来说，就是度量两个概率分布间的差异性信息，在某一程度上也可以防止梯度学习过慢，公式可见下，Pytorch调用函数有两个，一个是nn.BCELoss函数，用的时候要结合Sigmoid函数，另外一个是nn.BCEWithLogitsLoss()

import torch.nn as nn
import torchm = nn.Sigmoid()
loss = nn.BCELoss()
input = torch.randn(3, requires_grad=True)
target = torch.empty(3).random_(2)
output = loss(m(input), target)
print(output)

运行结果显示如下：

tensor(0.6214, grad_fn=<BinaryCrossEntropyBackward0>)

import torch
import torch.nn as nnlabel = torch.empty((2, 3)).random_(2)
x = torch.randn((2, 3), requires_grad=True)bce_with_logits_loss = nn.BCEWithLogitsLoss()
output = bce_with_logits_loss(x, label)print(output)

运行结果显示如下：

tensor(0.7346, grad_fn=<BinaryCrossEntropyWithLogitsBackward0>)

2.5 多分类交叉熵损失函数

也是度量两个概率分布间的差异性信息，Pytorch调用函数也有两个，一个是nn.NLLLoss，用的时候要结合log softmax处理，另外一个是nn.CrossEntropyLoss

import torch
import torch.nn.functional as Finput = torch.randn(3, 5, requires_grad=True)
target = torch.tensor([1, 0, 4])
output = F.nll_loss(F.log_softmax(input, dim=1), target)
print(output)

运行结果显示如下：

tensor(2.9503, grad_fn=<NllLossBackward0>)

import torch
import torch.nn as nnloss = nn.CrossEntropyLoss()
inputs = torch.randn(3, 5, requires_grad=True)
target = torch.empty(3, dtype=torch.long).random_(5)
output = loss(inputs, target)print(output)

运行结果显示如下：

tensor(1.6307, grad_fn=<NllLossBackward0>)

2.6 自定义损失

通过对 nn 模块进行子类化，将损失函数创建为神经网络图中的节点。这意味着我们的自定义损失函数是一个 PyTorch 层，与卷积层完全相同。

class Custom_MSE(nn.Module):def __init__(self):super(Custom_MSE, self).__init__();def forward(self, predictions, target):square_difference = torch.square(predictions - target)loss_value = torch.mean(square_difference)return loss_value# def __call__(self, predictions, target):#   square_difference = torch.square(y_predictions - target)#   loss_value = torch.mean(square_difference)#   return loss_value

可以在“forward”函数调用或“call”内部定义损失的实际实现。