towr code阅读

1. Introduction

towr是非常优美的足式机器人规划代码，通过阅读towr重要的几个迭代版本的代码深入了解。

2 v0.1

第一代的版本，foot的位置是提前给定的，只对COG的trajectory进行优化。

2.1 cost

公式
仅仅只考虑加速度，
$\int_0^T \ddot{x}^2(t)dt+v=q^TGq+v$

其中，
$\begin{bmatrix} a & b &c &d \end{bmatrix}^T$

在这里插入图片描述

代码

// 使用六阶多项式进行表示，有XY两个维度，需要优化的参数数目，用std::vecXd 表示
int n_coeff = splines.size() * kCoeffCount * kDim2d;
// 1e-12 < EndFCost < 1e-8, 初始值要非零
cf->M = EandFCost * Eigen::MatrixXd::Identity(cf->M.rows(), cf->M.cols()); // 初始化q和G的数据结构// 修改权重矩阵,将权重矩阵G进行分块，每一段占据一块，通过索引定位要对应的权重：X、Y、分段
for (const SplineInfo& s : splines) {std::array<double, 10> t_span = cache_exponents<10>(s.duration_);for (int dim = X; dim <= Y; dim++) {const int a  = var_index(s.id_, dim, A);const int b  = var_index(s.id_, dim, B);const int c  = var_index(s.id_, dim, C);const int d  = var_index(s.id_, dim, D);// for explanation of values see M.Kalakrishnan et al., page 248// "Learning, Planning and Control for Quadruped Robots over challenging// Terrain", IJRR, 2010// exact spline            cf->M(a, a) = 400.0 / 7.0      * t_span[7] * weight[dim];}
}
//具体每块的权重
cf->M(a, a) = 400.0 / 7.0      * t_span[7] * weight[dim];
cf->M(a, b) = 40.0             * t_span[6] * weight[dim];
cf->M(a, c) = 120.0 / 5.0      * t_span[5] * weight[dim];
cf->M(a, d) = 10.0             * t_span[4] * weight[dim];
cf->M(b, b) = 144.0 / 5.0      * t_span[5] * weight[dim];
cf->M(b, c) = 18.0             * t_span[4] * weight[dim];
cf->M(b, d) = 8.0              * t_span[3] * weight[dim];
cf->M(c, c) = 12.0             * t_span[3] * weight[dim];
cf->M(c, d) = 6.0              * t_span[2] * weight[dim];
cf->M(d, d) = 4.0              * t_span[1] * weight[dim];// mirrow values over diagonal to fill bottom left triangle
for (int c = 0; c < cf->M.cols(); ++c)for (int r = c + 1; r < cf->M.rows(); ++r)cf->M(r, c) = cf->M(c, r);

总结：标准QP类型，不需要提供Hessian 矩阵

2.2 equality constraints

Continuity and Goal Constraints
在QP问题上，表示为 $M * coe ff + v = 0$
位置、速度和加速度的约束
$\begin{bmatrix} a & b & c & d & e & f \end{bmatrix}^T + v = 0$
初始和终止状态约束code

// 计算constraints的数目
int coeff = splines.size() * kCoeffCount * kDim2d; // total number of all spline coefficients
int constraints = 0;
constraints += 2*4; // init {x,y} * {pos, vel, acc, jerk}
constraints += 2*3; // end  {x,y} * {pos, vel, acc, jerk}
constraints += (splines.size() - 1) * kDim2d * 4; // junctions {pos, vel, acc, jerk}
MatVecPtr ec(new MatVec(coeff, constraints, constraints));
// 满足初始状态
// positions at t = 0, M * V = cog
int f = var_index(0, dim, F);
ec->M(f, i) = 1.0;   // 权重
ec->v(i++) = -start_cog(dim);
// velocity set to zero
int e = var_index(0, dim, E);
ec->M(e, i) = 1.0;
ec->v(i++) = -kVelStart(dim);
// acceleration set to zero
int d = var_index(0, dim, D);
ec->M(d, i) = 2.0;
ec->v(i++) = -kAccStart(dim);
// jerk set to zero
int c = var_index(0, dim, C);
ec->M(c, i) = 6.0;
ec->v(i++) = -kJerkStart(dim);

终止状态的约束

 ec->M(last_spline + A, i) = t_duration[5];ec->M(last_spline + B, i) = t_duration[4];ec->M(last_spline + C, i) = t_duration[3];ec->M(last_spline + D, i) = t_duration[2];ec->M(last_spline + E, i) = t_duration[1];ec->M(last_spline + F, i) = 1;ec->v(i++) = -end_cog(dim);// velocityec->M(last_spline + A, i) = 5 * t_duration[4];ec->M(last_spline + B, i) = 4 * t_duration[3];ec->M(last_spline + C, i) = 3 * t_duration[2];ec->M(last_spline + D, i) = 2* t_duration[1];ec->M(last_spline + E, i) = 1;ec->v(i++) = -kVelEnd(dim);       // accelerationsec->M(last_spline + A, i) = 20 * t_duration[3];ec->M(last_spline + B, i) = 12 * t_duration[2];ec->M(last_spline + C, i) = 6 * t_duration[1];ec->M(last_spline + D, i) = 2;

连接点约束
初始点t=0; t_end = t_duration

int curr_spline = var_index(s, dim, A);
int next_spline = var_index(s+1, dim, A);// position of current spline at t_duration
ec->M(curr_spline + A, i) = t_duration[5];
ec->M(curr_spline + B, i) = t_duration[4];
ec->M(curr_spline + C, i) = t_duration[3];
ec->M(curr_spline + D, i) = t_duration[2];
ec->M(curr_spline + E, i) = t_duration[1];
ec->M(curr_spline + F, i) = 1;
// ...minus position of next spline at t=0...
ec->M(next_spline + F, i) = -1.0;
// ...must be zero
ec->v(i++) = 0.0;// velocity
ec->M(curr_spline + A, i) = 5 * t_duration[4];
ec->M(curr_spline + B, i) = 4 * t_duration[3];
ec->M(curr_spline + C, i) = 3 * t_duration[2];
ec->M(curr_spline + D, i) = 2 * t_duration[1];
ec->M(curr_spline + E, i) = 1;
ec->M(next_spline + E, i) = -1.0;
ec->v(i++) = 0.0;// acceleration
ec->M(curr_spline + A, i) = 20 * t_duration[3];
ec->M(curr_spline + B, i) = 12 * t_duration[2];
ec->M(curr_spline + C, i) = 6  * t_duration[1];
ec->M(curr_spline + D, i) = 2;
ec->M(next_spline + D, i) = -2.0;
ec->v(i++) = 0.0;// jerk (derivative of acceleration)
ec->M(curr_spline + A, i) = 60 * t_duration[2];
ec->M(curr_spline + B, i) = 24 * t_duration[1];
ec->M(curr_spline + C, i) = 6;
ec->M(next_spline + C, i) = -6.0;
ec->v(i++) = 0.0;

2.3 inequality constraints

质心在zmp安全范围内
将四组其中三个脚组成边缘

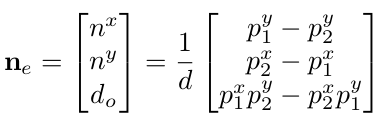
ZMP的作用位置

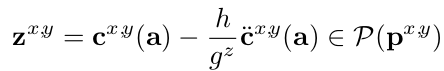
zmp到边缘的距离满足要求
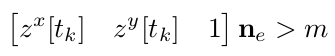
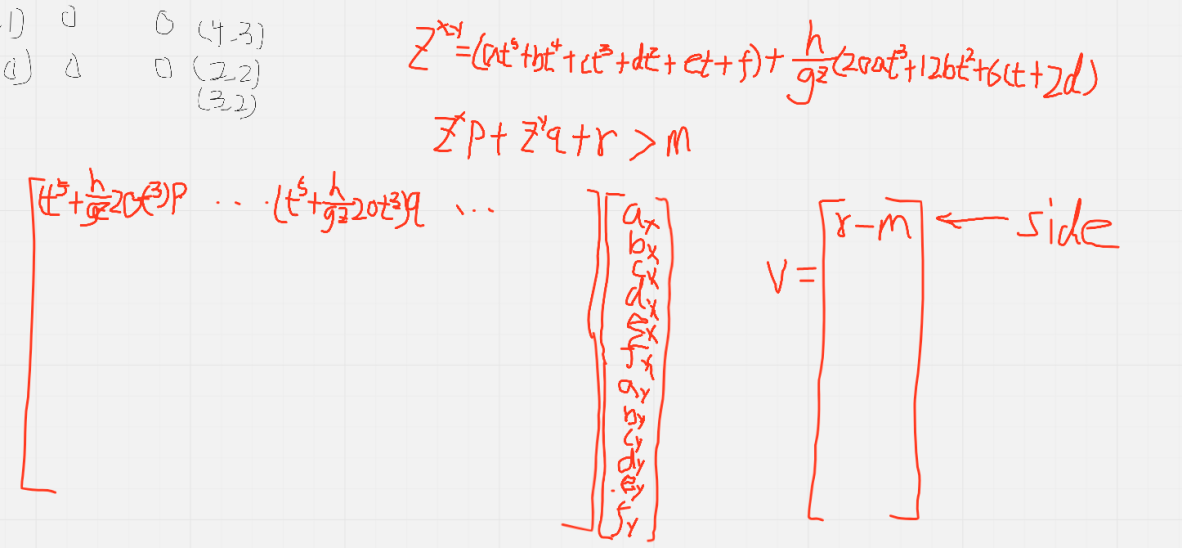
code

// 优化参数
int coeff = splines.size() * kCoeffCount * kDim2d;// calculate number of inequality constraints
double t_total = 0.0;
for (const SplineInfo& s : splines) t_total += s.duration_;int points = ceil(t_total / kDt);  // 离散化位置点
int constraints = points * 3; // 3 triangle side constraints per point，满足3个边缘要求
MatVecPtr ineq(new MatVec(coeff, constraints, constraints)); //不等式约束 Mq+v<=0// calculate zmp 
for (double time(0.0); time < s.duration_; time += kDt) {std::array<double,6> t = cache_exponents<6>(time);// one constraint per line of support trianglefor (SuppTriangle::TrLine l: lines) {double z_acc = 0.0; // TODO: calculate z_acc based on foothold heightconst int x = var_index(s.id_, X, A);const int y = var_index(s.id_, Y, A);ineq->M(x + A, c) = l.coeff.p * (t[5] - h/(g+z_acc) * 20.0 * t[3]);ineq->M(x + B, c) = l.coeff.p * (t[4] - h/(g+z_acc) * 12.0 * t[2]);ineq->M(x + C, c) = l.coeff.p * (t[3] - h/(g+z_acc) *  6.0 * t[1]);ineq->M(x + D, c) = l.coeff.p * (t[2] - h/(g+z_acc) *  2.0);ineq->M(x + E, c) = l.coeff.p *  t[1];ineq->M(x + F, c) = l.coeff.p *  1;ineq->M(y + A, c) = l.coeff.q * (t[5] - h/(g+z_acc) * 20.0 * t[3]);ineq->M(y + B, c) = l.coeff.q * (t[4] - h/(g+z_acc) * 12.0 * t[2]);ineq->M(y + C, c) = l.coeff.q * (t[3] - h/(g+z_acc) *  6.0 * t[1]);ineq->M(y + D, c) = l.coeff.q * (t[2] - h/(g+z_acc) *  2.0);ineq->M(y + E, c) = l.coeff.q *  t[1];ineq->M(y + F, c) = l.coeff.q *  1;ineq->v[c] = l.coeff.r - l.s_margin;++c;

2.4 参数配置

初始状态：
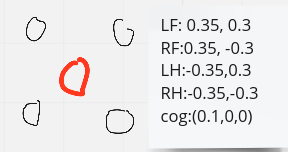
在这里插入图片描述
所有步态

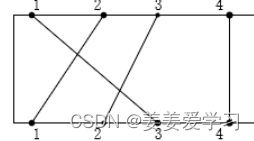
步态的时序
注意交叉的时候需要留出时间给cog进行调整

DEBUG xpp.zmp.zmpoptimizer : 
Spline: id= 0:	duration=0.60	four_leg_supp=0	step=0
Spline: id= 1:	duration=0.60	four_leg_supp=0	step=1
Spline: id= 2:	duration=0.20	four_leg_supp=1	step=2
Spline: id= 3:	duration=0.60	four_leg_supp=0	step=2
Spline: id= 4:	duration=0.60	four_leg_supp=0	step=3
Spline: id= 5:	duration=0.20	four_leg_supp=1	step=4
Spline: id= 6:	duration=0.60	four_leg_supp=0	step=4
Spline: id= 7:	duration=0.60	four_leg_supp=0	step=5
Spline: id= 8:	duration=0.20	four_leg_supp=1	step=6
Spline: id= 9:	duration=0.60	four_leg_supp=0	step=6
Spline: id= 10:	duration=0.60	four_leg_supp=0	step=7
Spline: id= 11:	duration=0.20	four_leg_supp=1	step=8

2.5 数据结构

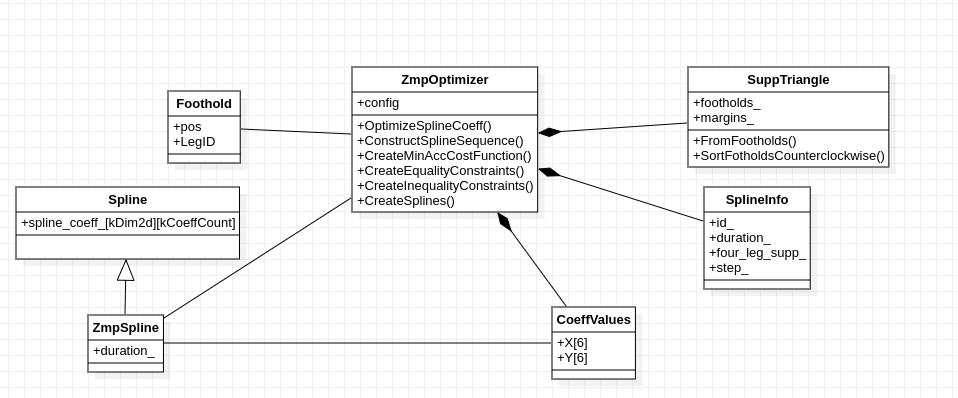
在这里插入图片描述

2.6 注意事项

在LH,LF,RH, RF, (LF,RH)切换的时候，机器人是四个腿全放在地面的，所以不会形成triangle
suppTriangles 的数量和splines的数量并不一致

SuppTriangles  SuppTriangle::FromFootholds(LegDataMap<Foothold> stance,const Footholds& steps,const MarginValues& margins, LegDataMap<Foothold>& last_stance)
{SuppTriangles tr;ArrayF3 non_swing;for (std::size_t s=0; s<steps.size(); s++) {LegID swingleg = steps[s].leg;// extract the 3 non-swinglegs from stanceint i = 0;for (LegID l : LegIDArray) if (stance[l].leg != swingleg)non_swing[i++] = stance[l];tr.push_back(SuppTriangle(non_swing, margins));stance[swingleg] = steps[s]; // update current stance with last step}last_stance = stance;::xpp::utils::logger_helpers::print_triangles(tr, log_);::xpp::utils::logger_helpers::PrintTriaglesMatlabInfo(tr, log_matlab_);return tr;   
}

但是在计算triangle的时候，这里没有考虑four-support的情况,four-support 不用考虑平衡

for (const SplineInfo& s : splines) {LOG4CXX_DEBUG(log_, "Calc inequality constaints of spline " << s.id_ << " of " << splines.size() << ", duration=" << std::setprecision(3) << s.duration_ << ", step=" << s.step_);// no constraints in 4ls phaseif (s.four_leg_supp_) continue;// TODO: insert support polygon constraints here instead of just // allowing the ZMP to be anywhere// cache lines of support triangle of current spline for efficiencySuppTriangle::TrLines3 lines = supp_triangles[s.step_].CalcLines();  // 仍然使用上一次swing的triangle

2.7 代码的技巧

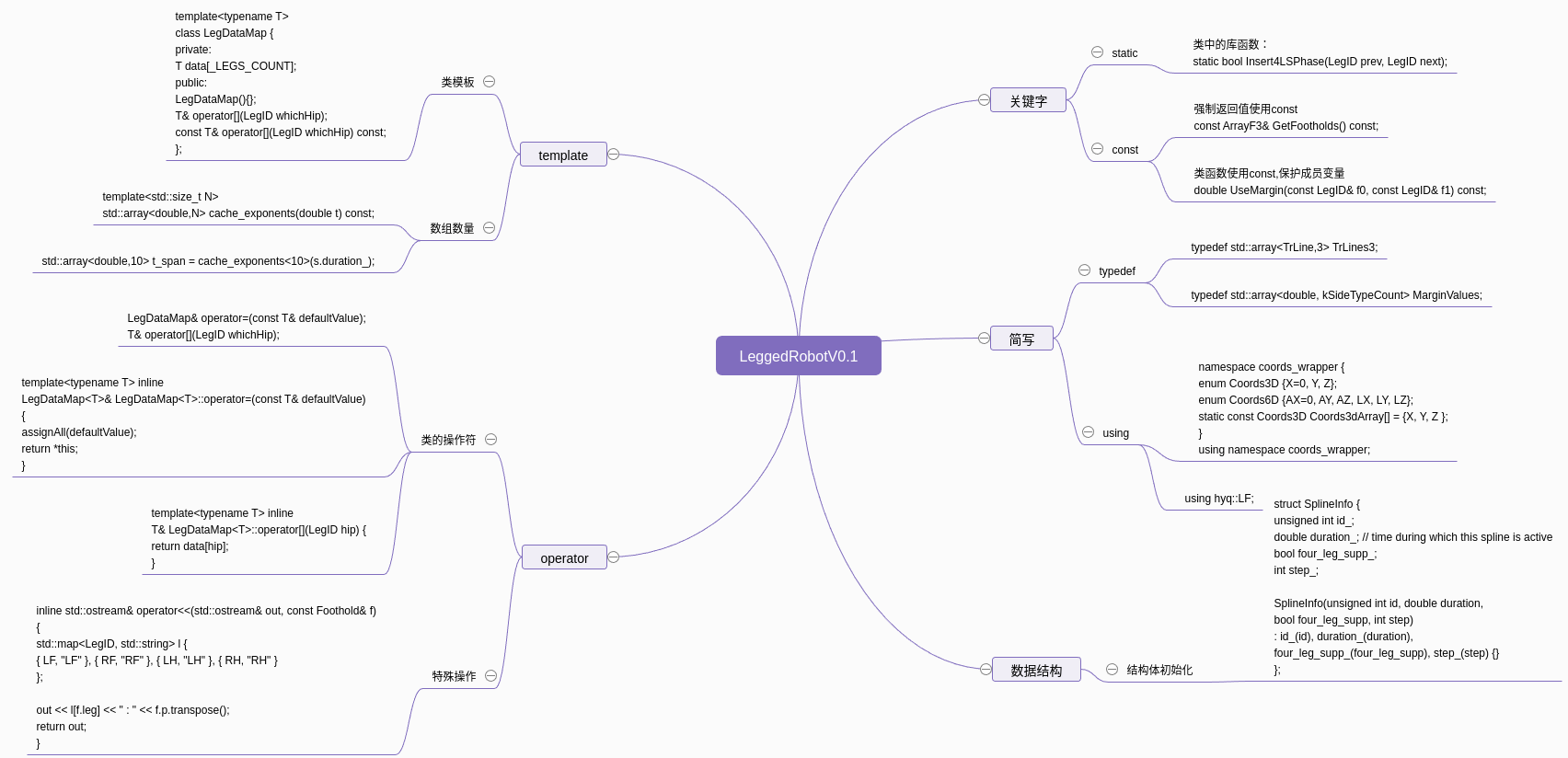
在这里插入图片描述

3 v0.2

第二版中最主要的改变是将6阶spline中只优化其中四个参数，提高了运算速度。

3.1 优化器设置

所要优化的参数变量

3.1.1 cost

仍然采用二阶积分，计算cost.

    for (const SplineInfo& s : spline_infos_) {std::array<double, 10> t_span = cache_exponents<10>(s.duration_);for (int dim = X; dim <= Y; dim++) {const int a  = var_index(s.id_, dim, A);const int b  = var_index(s.id_, dim, B);const int c  = var_index(s.id_, dim, C);const int d  = var_index(s.id_, dim, D);// for explanation of values see M.Kalakrishnan et al., page 248// "Learning, Planning and Control for Quadruped Robots over challenging// Terrain", IJRR, 2010// exact spline            cf->M(a, a) = 400.0 / 7.0      * t_span[7] * weight[dim];cf->M(a, b) = 40.0             * t_span[6] * weight[dim];cf->M(a, c) = 120.0 / 5.0      * t_span[5] * weight[dim];cf->M(a, d) = 10.0             * t_span[4] * weight[dim];cf->M(b, b) = 144.0 / 5.0      * t_span[5] * weight[dim];cf->M(b, c) = 18.0             * t_span[4] * weight[dim];cf->M(b, d) = 8.0              * t_span[3] * weight[dim];cf->M(c, c) = 12.0             * t_span[3] * weight[dim];cf->M(c, d) = 6.0              * t_span[2] * weight[dim];cf->M(d, d) = 4.0              * t_span[1] * weight[dim];  // mirrow values over diagonal to fill bottom left trianglefor (int c = 0; c < cf->M.cols(); ++c) for (int r = c+1; r < cf->M.rows(); ++r)cf->M(r, c) = cf->M(c, r);          }}

3.1.2 equality constraints

连接点只考虑加速度和速度
初始对应的速度和位置通过参数给定start_p 和start_v进行导入

constraints += kDim2d*2;                         // init {x,y} * {acc, jerk} pos, vel implied
constraints += kDim2d*3;                         // end  {x,y} * {pos, vel, acc}
constraints += (spline_infos_.size()-1) * kDim2d * 2;  // junctions {acc,jerk} since pos, vel  implied

初始状态,不对初始位置速度进行限制了
$f(x)=At^5+Bt^4+Ct^3+Dt^2+Et+F$
只对加速度和jerk进行限制
$\begin{bmatrix} 0 & 0 & 0 & 2.0 \\ 0 & 0 & 6 & 0 \end{bmatrix} \begin{bmatrix} A \\ B \\ C \\D \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}$
代码：

// acceleration set to zero
int d = var_index(0, dim, D);
ec->M(d, i) = 2.0;
ec->v(i++) = -kAccStart(dim);
// jerk set to zero
int c = var_index(0, dim, C);
ec->M(c, i) = 6.0;
ec->v(i++) = -kJerkStart(dim);

终止状态
var_index(int spline, int dim, int coeff) 对应结果
$n = s pl in e * k D im 2 d * coe ff + d im * coe ff + coe ff$
DescribeEByPrev的计算效果
$\begin{aligned} Ek & = \begin{bmatrix} 5t_0^4 & 4t_0^3 & 3t_0^2 & 2t_0 & ... & 5t_i^4 & 4t_i^3 & 3t_i^2 & 2t_i & ... & 5t_{n-1}^4 & 4t_{n-1}^3 & 3t_{n-1}^2 & 2t_{n-1} \end{bmatrix} \\ nondependent & = startcogv \end{aligned}$
考虑到隐含关系
$\begin{aligned} 5A_it_i^4+4B_it_i^3+3C_it_i^2+2D_it_i+E_i &=E_{i+1} \\ Coeff * Ek&=\sum_i^{n-1}E_{i+1}-E_{i}=E_n-E_0 \\ nondependent & = E_0 \\ Coeff*Ek+nondependent &=E_n \end{aligned}$
DescribeFByPrev的计算效果
$\begin{aligned} Fk & = \begin{bmatrix} 5t_0^4+\sum_0^k5t_0^4t_i & 4t_0^3+ \sum_0^k4t_0^3t_i & ... & 3t_0^2+\sum_0^k3t_0^2t_i & 2t_0+ \sum_0^k2t_0t_i \\ 5t_1^4+\sum_1^k5t_1^4t_i & 4t_1^3+ \sum_1^k4t_1^3t_i & ... & 3t_1^2+\sum_1^k3t_1^2t_i & 2t_1+ \sum_1^k2t_1t_i \end{bmatrix} \\ nondependent & = startcogv * \sum t_i+startcogp \\ \end{aligned}$
考虑到位置隐含关系
$\begin{aligned} A_it_i^5+B_it_i^4+C_it_i^3+D_it_i^2+E_it_i+F_i &=F_{i+1} \\ \sum_0^{i-1}(5A_jt_j^4t_i+4B_jt_j^3t_i+3D_jt_j^2t_i+2D_jt_jt_i) & = \sum_0^{i-1}(E_{j+1}-E_j)t_i=(E_{i}-E_0)t_i \\ Coeff * Fk&=\sum_i^{n-1}(F_{i+1}-F_{i}-E_it_i+E_it_i-E_0t_i)=F_n-F_0-E_0t_{sum} \\ nondependent & = E_0t_{sum}+F_0 \\ Coeff * Fk+nondependent &=F_n \end{aligned}$

借助DescribeEByPrev和DescribeFByPrev，同样可以计算pos和velocity对应的数值

对于终止位置
$\begin{aligned} (Coeff*Ek+nondependente)*t_n+ & \\(Coeff*Fk+nondependentf) +(end_P-E_nt_n-F_n)& = \\ & = E_n*t_n+ F_n+(end_P-E_nt_n-F_n) \\ & = end_P \end{aligned}$
对于终止速度
$\begin{aligned} (Coeff*Ek+nondependente)+ & \\(end_V-E_n)& = \\ & = E_n+(end_v-E_n) \\ & = end_V \end{aligned}$
对于加速度不需要借助DescribeFByPrev和DescribeEByPrev

// 2. Final conditions
int K = spline_infos_.back().id_; // id of last spline
int last_spline = var_index(K, dim, A);
std::array<double,6> t_duration = cache_exponents<6>(spline_infos_.back().duration_);// calculate e and f coefficients from previous values
Eigen::VectorXd Ek(coeff); Ek.setZero();
Eigen::VectorXd Fk(coeff); Fk.setZero();
double non_dependent_e, non_dependent_f;
DescribeEByPrev(K, dim, start_cog_v(dim), Ek, non_dependent_e);
DescribeFByPrev(K, dim, start_cog_v(dim), start_cog_p(dim), Fk, non_dependent_f);// position 
ec->M(last_spline + A, i) = t_duration[5];
ec->M(last_spline + B, i) = t_duration[4];
ec->M(last_spline + C, i) = t_duration[3];
ec->M(last_spline + D, i) = t_duration[2];
ec->M.col(i) += Ek*t_duration[1];
ec->M.col(i) += Fk;ec->v(i)     += non_dependent_e*t_duration[1] + non_dependent_f;
ec->v(i++) = -end_cog(dim);// velocity
ec->M(last_spline + A, i) = 5 * t_duration[4];
ec->M(last_spline + B, i) = 4 * t_duration[3];
ec->M(last_spline + C, i) = 3 * t_duration[2];
ec->M(last_spline + D, i) = 2* t_duration[1];
ec->M.col(i) += Ek;ec->v(i)     += non_dependent_e;
ec->v(i++)   += -kVelEnd(dim);       // accelerations
ec->M(last_spline + A, i) = 20 * t_duration[3];
ec->M(last_spline + B, i) = 12 * t_duration[2];
ec->M(last_spline + C, i) = 6 * t_duration[1];
ec->M(last_spline + D, i) = 2;ec->v(i++) = -kAccEnd(dim);

连接点状态
连接点状态因为没有位置和速度约束和v0.1的一样

for (SplineInfoVec::size_type s = 0; s < spline_infos_.size() - 1; ++s)
{std::array<double,6> t_duration = cache_exponents<6>(spline_infos_.at(s).duration_);for (int dim = X; dim <= Y; dim++) {int curr_spline = var_index(s, dim, A);int next_spline = var_index(s + 1, dim, A);// accelerationec->M(curr_spline + A, i) = 20 * t_duration[3];ec->M(curr_spline + B, i) = 12 * t_duration[2];ec->M(curr_spline + C, i) = 6  * t_duration[1];ec->M(curr_spline + D, i) = 2;ec->M(next_spline + D, i) = -2.0;ec->v(i++) = 0.0;// jerk (derivative of acceleration)ec->M(curr_spline + A, i) = 60 * t_duration[2];ec->M(curr_spline + B, i) = 24 * t_duration[1];ec->M(curr_spline + C, i) = 6;ec->M(next_spline + C, i) = -6.0;ec->v(i++) = 0.0;}
}

3.1.3 inequality constraints

ZMP的作用位置

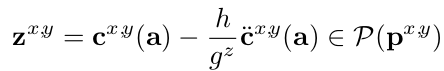
zmp到边缘的距离满足要求
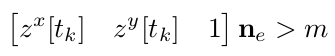
在这里插入图片描述
$\begin{aligned} Z_x*l.p+Z_y*l_q+r-m &>0 \\ z &= pos_t-E_i*t-F_i+(Coeff*EK+E_0)*t+ \\ &(Coeff*FK+nondeF)-\frac{h}{g_{zacc}}*acc_t \end{aligned}$

for (double i=0; i < std::floor(s.duration_/kDt); ++i) {double time = i*kDt;std::array<double,6> t = cache_exponents<6>(time);// one constraint per line of support trianglefor (SuppTriangle::TrLine l: lines) {// the zero moment point must always lay on one side of triangle side:// p*x_zmp + q*y_zmp + r > stability_margin// with: x_zmp = x_pos - height/(g+z_acc) * x_acc//       x_pos = at^5 +   bt^4 +  ct^3 + dt*2 + et + f//       x_acc = 20at^3 + 12bt^2 + 6ct   + 2ddouble z_acc = 0.0; // TODO: calculate z_acc based on foothold heightfor (int dim=X; dim<=Y; dim++) {double lc = (dim==X) ? l.coeff.p : l.coeff.q;// calculate e and f coefficients from previous valuesEigen::VectorXd Ek(coeff); Ek.setZero();Eigen::VectorXd Fk(coeff); Fk.setZero();double non_dependent_e, non_dependent_f;DescribeEByPrev(k, dim, start_cog_v(dim), Ek, non_dependent_e);DescribeFByPrev(k, dim, start_cog_v(dim), start_cog_p(dim), Fk, non_dependent_f);ineq->M(var_index(k,dim,A), c) = lc * (t[5] - h/(g+z_acc) * 20.0 * t[3]);ineq->M(var_index(k,dim,B), c) = lc * (t[4] - h/(g+z_acc) * 12.0 * t[2]);ineq->M(var_index(k,dim,C), c) = lc * (t[3] - h/(g+z_acc) *  6.0 * t[1]);ineq->M(var_index(k,dim,D), c) = lc * (t[2] - h/(g+z_acc) *  2.0);ineq->M.col(c) += lc * Ek*t[1];ineq->M.col(c) += lc * Fk;ineq->v[c]     += lc *(non_dependent_e*t[0] + non_dependent_f);}ineq->v[c] += l.coeff.r - l.s_margin;++c;}
}
}

3.2 轨迹优化的流程

ConstructSplineSequence->optCeff->generateTraj
逻辑和之前一样，但是处理更加漂亮

double discretization_time = 0.1; 
double swing_time = 0.6;         
double stance_time = 0.2;         
double t_stance_initial = 1.0; //sint step = 0;
unsigned int id = 0; // unique identifiers for each splineconst int kSplinesPer4ls = 1;
const int kSplinesPerStep = 1;// 人为的建立抬脚的step sequences:延长了初始和结束的时间1s
for (size_t i = 0; i < step_sequence.size(); ++i) {// 1. insert 4ls-phase when switching between disjoint support triangles// Attention: these 4ls-phases much coincide with the ones in the zmp optimizer        if (i == 0) { // never insert 4ls-phase before first stepspline_infos_.push_back(SplineInfo(id++, t_stance_initial, true, step));} else {LegID swing_leg = step_sequence[i]; // 按照顺序进行抬腿LegID swing_leg_prev = step_sequence[i-1];if (SuppTriangle::Insert4LSPhase(swing_leg_prev, swing_leg)) {for (int s = 0; s < kSplinesPer4ls; s++) spline_infos_.push_back(SplineInfo(id++, t_stance/kSplinesPer4ls, true, step));}}// insert swing phase splinesfor (int s = 0; s < kSplinesPerStep; s++) spline_infos_.push_back(SplineInfo(id++, t_swing/kSplinesPerStep, false, step));// always have last 4ls spline for robot to move into center of feetif (i==step_sequence.size()-1) spline_infos_.push_back(SplineInfo(id++, t_stance_final, true, step));step++;
}