动态规划（Dynamic Programming，简称DP）是一种在数学、计算机科学和经济学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题，它能够将问题分解为相互独立的子问题，并将子问题的解存储起来，以便下次需要时直接使用，从而减少计算量，提高效率。最经典的例子就是0-1背包问题。

0-1背包问题描述：给定一组物品，每种物品都有自己的重量和价值，在限定的总重量内，选取若干种物品，使得物品的总价值最大。其中，每种物品只能选择一次或不选择。
 

基本思路

用子问题定义状态：f[i][c] 表示前 i 件物品放入一个容量为 c 的背包可以获得的最大价值。第 i 件物品的重量是 wi，价值是 vi，则其状态转移方程是：

f[i][c] = max(f[i-1][c], f[i-1][c-wi] + vi)

这个方程非常重要，基本上所有跟背包相关的问题的方程都是由它衍生出来的。分析子问题“将前 i 件物品放入容量为 c 的背包中”，考虑第 i 件物品放或不放入背包，可以转化为一个只牵扯前 i-1 件物品的问题：如果不放第 i 件物品，那么问题就转化为“前 i-1 件物品放入容量为 c 的背包中”，价值为 f[i-1][c]；如果放第 i 件物品，那么问题就转化为“前 i-1 件物品放入剩下的容量为 c-wi 的背包中”，此时能获得的最大价值就是 f[i-1][c-wi] 再加上通过放入第 i 件物品获得的价值 vi。所以按照这个方程递推完毕后，最终的答案一定是 f[i][c]。

示例程序

def knapsack(items, capacity):n = len(items)f = [[0 for _ in range(capacity + 1)] for _ in range(n + 1)]# f[i][c] 表示在前i个物品中选择若干个物品放入容量为c的背包中所能获得的最大价值for i in range(1, n + 1):  # 遍历物品wi, vi = items[i-1]for c in range(1, capacity + 1):  # 遍历容量if c < wi:# 当前容量小于当前物品的重量，无法放入该物品，保持背包现状# 即：上一轮遍历物品的循环中同样数量物品的最大价值，所以是 f[i-1][c]f[i][c] = f[i-1][c]else:# 可以放入，判断放入该物品是否能使背包中物品价值最大# 如果放入，可能需要腾出背包中同样重量的物品，所以是 f[i-1][c-wi]# 然后 f[i-1][c-wi] + vi 得到放入该物品后的价值# 不放入该物品（保持背包现状），与放入该物品，取两者中的最大值f[i][c] = max(f[i-1][c], f[i-1][c-wi] + vi)return f[n][capacity]items = [(2, 3), (2, 2), (1, 2), (3, 6)]  # 物品列表，每个元素表示该物品的重量和价值
capacity = 3  # 背包的容量限制
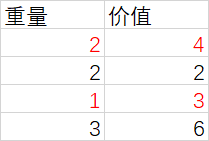
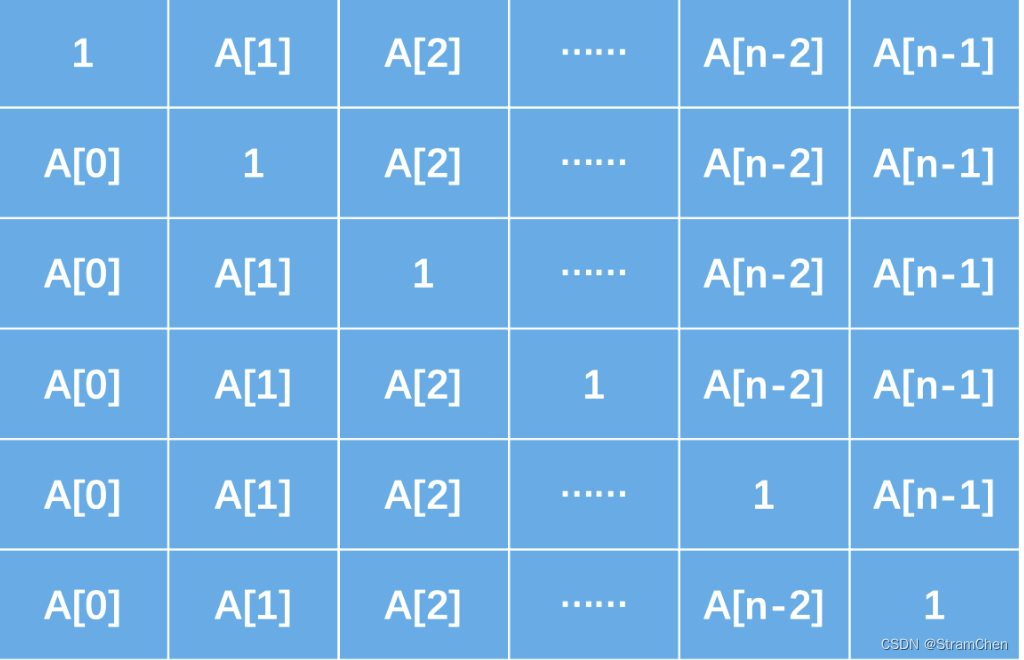
print(knapsack(items, capacity))

上面的例子中，有 4 个物品，其重量和价值分别是 (2, 3), (2, 2), (1, 2), (3, 6)，背包容量为 3，程序输出 6，即：选择若干个物品放入该背包中所能获得的最大价值是 6。为直观显示，将数据以表格形式展示如下：

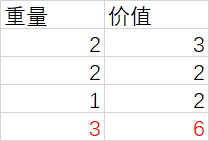
修改测试数据，第一个物品和第三个物品的价值各增加 1，这两个物品重量之和为 3，刚好放入背包，价值为 7 超过之前第 4 个物品的价值 6，程序输出 7。以表格形式展示如下：