改进YOLOv8：结合ICCV2023｜动态蛇形卷积，构建不规则目标识别网络

🔥🔥🔥 提升多尺度、不规则目标检测，创新提升 🔥🔥🔥

🔥🔥🔥 捕捉图像特征和处理复杂图像特征 🔥🔥🔥

👉👉👉: 本专栏包含大量的新设计的创新想法，包含详细的代码和说明，具备有效的创新组合，可以有效应用到改进创新当中 👉👉👉:

🐤🐤🐤

改进YOLOv8：结合ICCV2023｜动态蛇形卷积，构建不规则目标识别网络

  • 研究概括
  • 动态蛇卷积(DSConv)
  • 代码使用
  • 构建蛇形动态预测网络

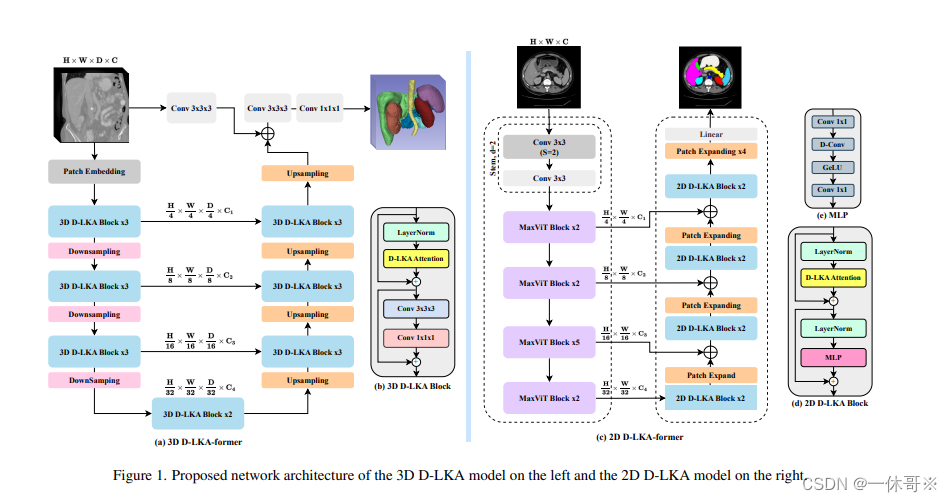
在这里插入图片描述

研究概括

在这里插入图片描述

论文《DSCNet: Disentangling tube Structure Segmentation with Dynamic Snake Convolution》提出了一种新的DSCNet框架，用于血管、道路等图像中管状结构的分割。该

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/187913.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

《算法通关村——透彻理解二叉树中序遍历的应用》

《算法通关村——透彻理解二叉树中序遍历的应用》

《算法通关村——透彻理解二叉树中序遍历的应用》 直接上题 108. 将有序数组转换为二叉搜索树 给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。 高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高…
阅读更多...
屏幕提词软件Presentation Prompter mac中文版使用方法

屏幕提词软件Presentation Prompter mac中文版使用方法

Presentation Prompter for mac是一款屏幕提词器软件，它可以将您的Mac电脑快速变成提词器，支持编写或导入，可以在一个或多个屏幕上平滑地滚动，Presentation Prompter 下载是为适用于现场表演者，新闻广播员，…
阅读更多...
【Hadoop实战】Hadoop指标系统V2分析

【Hadoop实战】Hadoop指标系统V2分析

Hadoop指标系统V2分析 文章目录 Hadoop指标系统V2分析架构主要组成部分根据图表解释数据流向指标过滤JMX的应用开启指标系统的组件指标项说明 使用HTTP（JMXJsonServlet）获取指标接口调用方式GET查询的逻辑数据的来源，以及更新的原理 架构 在…
阅读更多...
arcsinx的导数

arcsinx的导数

阅读更多...
【uni-app + uView】CountryCodePicker 国家区号组件

【uni-app + uView】CountryCodePicker 国家区号组件

1. 效果图 2. 组件完整代码 <template><u-popup class="country-code-picker-container" v-if="show" :show
阅读更多...
Oracle递归查询树形数据

Oracle递归查询树形数据

实际生活有很多树形结构的数据&#xff0c;比如公司分为多个部门、部门下分为多个组&#xff0c;组下分为多个员工&#xff1b;省市县的归属&#xff1b;页面菜单栏等等。 如果想查询某个节点的父节点或者子节点&#xff0c;一般通过表自身连接完成&#xff0c;但如果该节点的子…
阅读更多...
virtualBox虚拟机局域网访问配置

virtualBox虚拟机局域网访问配置

在VirtualBox中&#xff0c;桥接网络是一种网络连接类型&#xff0c;它允许虚拟机连接到物理网络上的路由器或交换机&#xff0c;在物理网络上获得独立的网络地址和访问权限。 一、设置VirtualBox桥接网络的步骤&#xff1a; 打开VirtualBox软件&#xff0c;并选择你想要配置…
阅读更多...
基于若依的ruoyi-nbcio流程管理系统仿钉钉流程json转bpmn的flowable的xml格式（支持并行网关）

基于若依的ruoyi-nbcio流程管理系统仿钉钉流程json转bpmn的flowable的xml格式（支持并行网关）

更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码&#xff1a; https://gitee.com/nbacheng/ruoyi-nbcio 演示地址&#xff1a;RuoYi-Nbcio后台管理系统 这个章节来完成并行网关&#xff0c;前端无需修改&#xff0c;直接后端修改就可以了。 1、并行网关后端修…
阅读更多...
python升级pip的时候一直失败

python升级pip的时候一直失败

如图,一直提示使用 python.exe -m pip install --upgrade pip 进行升级pip,但是执行这句命令又不成功.然后综合了几篇文章以后使用了下面的命令可以升级了 python -m pip install --upgrade pip --user -i https://mirrors.aliyun.com/pypi/simple/ 主要是在推荐的语句上使用…
阅读更多...
已解决：云原生领域的超时挂载Bug — Kubernetes深度剖析

已解决：云原生领域的超时挂载Bug — Kubernetes深度剖析

&#x1f337;&#x1f341; 博主猫头虎&#xff08;&#x1f405;&#x1f43e;&#xff09;带您 Go to New World✨&#x1f341; &#x1f984; 博客首页——&#x1f405;&#x1f43e;猫头虎的博客&#x1f390; &#x1f433; 《面试题大全专栏》 &#x1f995; 文章图文…
阅读更多...
Ubuntu18.04.6安装qt5.7.1（超级详细教程）

Ubuntu18.04.6安装qt5.7.1（超级详细教程）

目录 1、下载对应Linux版本的qt 2、安装完qt&#xff0c;可能也要安装下对应的编译工具 1、下载对应Linux版本的qt &#xff08;1&#xff09;准备安装的是qt5.7.1&#xff1a;qt-opensource-linux-x64-5.7.1.run &#xff08;2&#xff09;在虚拟机进入存放qt安装包的目录…
阅读更多...
QT QDockWidget

QT QDockWidget

QDockWidget是Qt中的一个容器类&#xff0c;用于在主窗口上创建可停靠的子窗口。 设置停靠窗口的一般流程如下: (1)创建一个QDockWidget 对象的停靠窗体。 (2)设置此停靠窗体的属性&#xff0c;通常调用setFeatures()及setAllowedAreas()两种方法。 (3)新建一个要插入停靠窗…
阅读更多...
消息队列使用场景

消息队列使用场景

&#x1f388;个人公众号:&#x1f388; :✨✨✨ 可为编程✨ &#x1f35f;&#x1f35f; &#x1f511;个人信条:&#x1f511; 知足知不足 有为有不为 为与不为皆为可为&#x1f335; &#x1f349;本篇简介:&#x1f349; 本篇记录消息队列使用场景&#xff0c;如有出入还望…
阅读更多...
C++ 配合图形库实现画线效果

C++ 配合图形库实现画线效果

#include<stdio.h> #include <conio.h> #include<math.h> #include <graphics.h> // 引用图形库头文件 #define N 12 int List[N][N];void draw() {for (int i 0; i < N; i) {int x 200 * cos(2 * 3.14 * i / N);int y 200 * sin(2 * 3.1…
阅读更多...
面试复习整理

面试复习整理

redis持久化方式和原理 Redis持久化是指将Redis内存中的数据以某种形式保存到磁盘上&#xff0c;以保证在Redis重启后数据不会丢失。Redis支持两种持久化方式&#xff1a;RDB&#xff08;Redis DataBase&#xff09;和AOF&#xff08;Append Only File&#xff09;。 RDB持久…
阅读更多...
刷题学习记录BUUCTF

刷题学习记录BUUCTF

[极客大挑战 2019]RCE ME1 进入环境直接就有代码 <?php error_reporting(0); if(isset($_GET[code])){$code$_GET[code];if(strlen($code)>40){die("This is too Long.");}if(preg_match("/[A-Za-z0-9]/",$code)){die("NO.");}eval($co…
阅读更多...
使用Vite创建Vue3项目 配置路由+路径（包教包会）

使用Vite创建Vue3项目 配置路由+路径（包教包会）

使用Vite创建Vue3项目 配置路由路径 一、创建项目&#xff1a;二、配置路由1. vue3vitets路由配置2. vue3vitejs路由配置 三、配置路径 一、创建项目&#xff1a; 创建一个文件夹在文件夹上的 地址栏 或者是 winR 打开cmd命令窗口。 输入命令 npm create vitelatest 这里我们…
阅读更多...
杂记杂记杂记

杂记杂记杂记

Mybatis分页插件原理&#xff1f; 首先分页参数放到ThreadLocal中&#xff0c;拦截执行得到sql&#xff0c;根据数据库类型添加对应的分页语句将重写sql。例如&#xff1a;&#xff08;select * from table where a&#xff09;转换为 &#xff08;select count(*) from table…
阅读更多...
Ubuntu 20.04编译Chrome浏览器

Ubuntu 20.04编译Chrome浏览器

本文记录chrome浏览器编译过程&#xff0c;帮助大家避坑qaq 官网文档&#xff1a;https://chromium.googlesource.com/chromium/src//main/docs/linux/build_instructions.md 一.系统要求 一台64位的英特尔机器&#xff0c;至少需要8GB的RAM。强烈推荐超过16GB。至少需要100…
阅读更多...
蓝桥杯每日一题2023.11.10

蓝桥杯每日一题2023.11.10

“蓝桥杯”练习系统 (lanqiao.cn) 题目描述 题目分析 对于此题&#xff1a;我们看到题目要求尽可能大&#xff0c;会联想到二分&#xff0c;注意切出的一定为正方形&#xff0c;其能切出的个数为(h[i] / x) * (w[i] / x)&#xff0c;将所有的个数与要求的个数进行对比&#x…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023