目录
1.匿名函数
1.1.匿名函数的定义与分类
1.2.匿名函数在积分和优化中应用
2.嵌套函数
2.1.嵌套函数的定义与分类
2.2.嵌套函数彼此调用关系
2.3.嵌套函数在积分和微分中应用
3.微分和积分
4.蒙特卡洛法
4.1.圆周率的模拟
4.2.计算N重积分(均匀分布)
4.3.计算N重积分(等序列分布)
1.匿名函数
1.1.匿名函数的定义与分类
匿名函数(Anonymous function)
定义:f = @(X)expr
x为指定的函数的自变量,Expr为具体的函数表达式。
f = @(x) x.^2; ff = f(1:10) ff = 1 4 9 16 25 36 49 64 81 100 g = @(x,y) x.^2 + y.^2; gg = g(1:4,2:5) gg = 5 13 25 41
单变量匿名函数
定义:f =@(x) expr
-
x为指定函数的自变量,Expr为具体的函数表达式
f = @(x) x.^2
-
含有参数的匿名函数,当参数已知的时候
a = 10, b = 20; f = @(x) a*x.^2+b; f(1:5) ans = 30 60 110 180 270
-
多变量匿名函数
g = @(x,y) x.^2+y.^2; % 含有参数的匿名函数,当参数已知的时候 a = 1,b = 2; f = @(x,y) a*x.^2+b*y; f(1:5,2:6) ans = 5 10 17 26 37
多重匿名函数
只有一个@符号的为单重匿名函数;有多个@符号的为二重、多重匿名函数,在参数传递方面非常方便。例:简单的二重匿名函数
f = @(a,b) @(x) a*x.^2+b*x+2; f(2,3) ans = @(x) a*x.^2+b*x+2 ans(3) ans = 29
这个段代码有一点问题,运行结果是17
改成下面的代码才是正确的输出:29
多重匿名函数
f = @(a) a(b,c) @(x) a*x.^2+b*x+c;
匿名函数在解方程中的应用
匿名函数可以非常方便地表达所求方程,并提供fzero等函数调用。例1:求下列方程的根
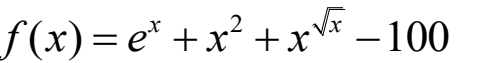
f = @(x) exp(x) + x.^2 + x.^(sqrt(x)) - 100; x0 = fzero(f,3) x0 =4.1635 f(x0) ans =2.8422e-14
匿名函数在解方程中的应用
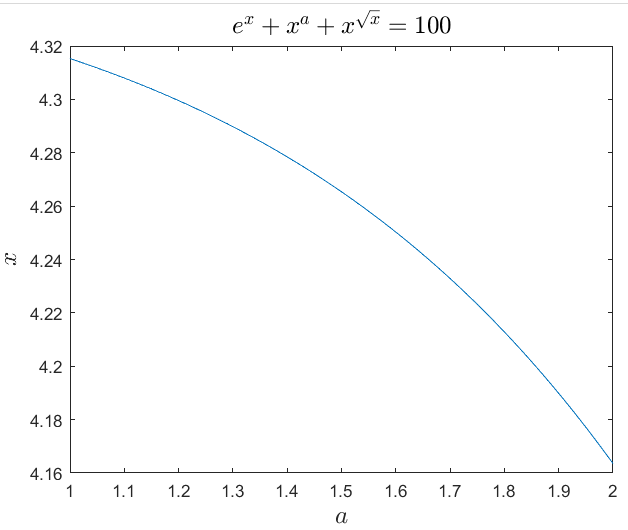
不同参数一一求解对应方程的根时,调用arrayfun函数。例1续:a = [0, 0.01, 0.02, ...., 2]求下列方程相应的根,画出a和相应的x的图像。
f = @(a) @(x) exp(x) + x^a + x^(sqrt(x)) - 100;
aa = 1:0.01:2;
y = arrayfun(@(a) fzero(f(a), 4), aa);
%运用arrayfun函数批量处理
plot(aa, y)
xlabel('$a$','interpreter','latex','fontsize',15)
ylabel('$x$','interpreter','latex','fontsize',15)
title('$e^x+x^a+x^{\sqrt{x}}=100$','interpreter','latex','fontsize',15)
匿名函数在表示隐函数方面的应用
隐函数一般无数学上的显式表示,运用matlab,对自变量x运用数值解给出因变量y。
例1:显式表示下列y关于x的隐函数
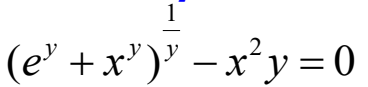
y = @(x) fzero(@(y)(exp(y)+x^y)^(1/y)-x^2*y,1); y(1) ans =2.7779
希望接受向量形式的输入,结合arrayfun函数
y = @(x) arrayfun(@(xx)fzero(@(y)(exp(y)+xx^y)^(1/y)-xx^2*y,1),x); y(1:5) ans =2.7779 1.1055 0.7759 0.6284 0.5425
例2:显式表示Z关于x,y的函数
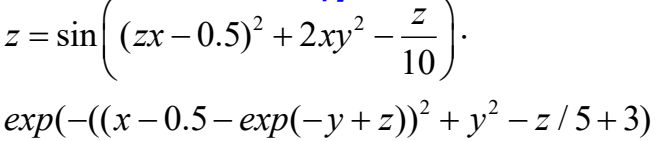
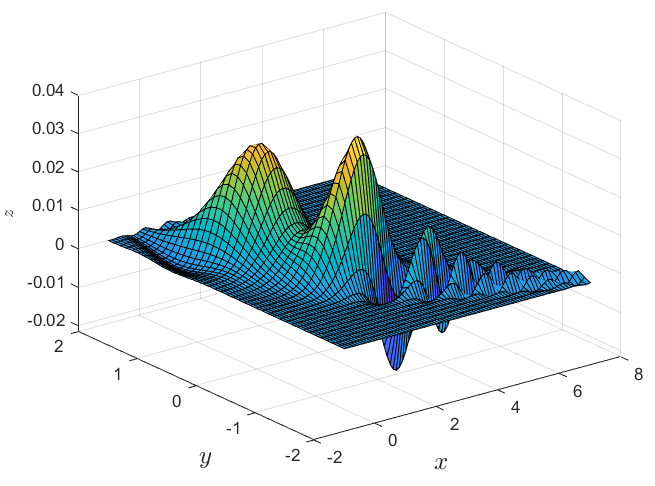
接受向量形式的输入,结合arrayfun、fzero函数
z = @(x,y) fzero(@(z)z-sin((z*x-0.5*)^2+2*x*y^2-z/10)*exp(-((x-0.5-exp(-y+z))^2+y^2-z/5+3)),rand);
[X,Y] = meshgrid(-1:0.1:7,-2:0.1:2);
Z = arrayfun(@(x,y) z(x,y), X, Y)
surf(X, Y, Z)
%坐标轴和函数标题
xlabel('$x$','interpreter','latex','fontsize',15)
ylabel('$y$','interpreter','latex','fontsize',15)
zlabel('$z$','interpreter','latex','fontszie',15)
title('$z=\sin((zs-0.5)^2+zxy^2-z/10)\exp(-((x-0.5-\exp(-y+z))^2+y^2-z/5+3))$','interpreter','latex','fontsize',15)
1.2.匿名函数在积分和优化中应用
匿名函数在求积分区域中的应用
在对称区间积分,求积分区间[-t,t],使得
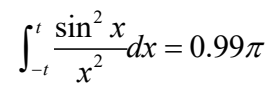
z=fzero(@(u) 0.99*pi/2-quadl(@(x)sin(x).^2./x.^2, 0, u), 1) z =32.3138
匿名函数在数值积分中的应用
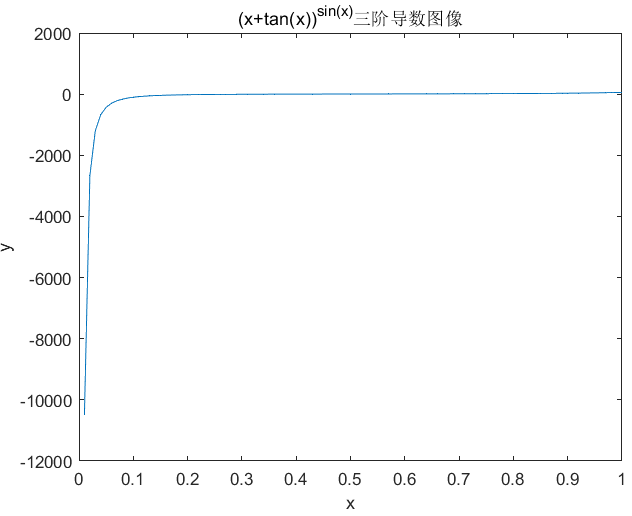
求下列函数的三阶导数在区间[0,1]上的图像
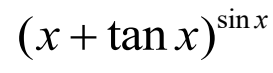
syms x;
f=(x+tan(x))^sin(x);
c=diff(f,3);
t=0:0.01:1;
f3=eval(['@(x)' vectorize(c)]);
plot(t,f3(t))
xlabel('x')
ylabel('y')
title('(x+tan(x))^{sin(x)}三阶导数图像')
三节导函数的图像
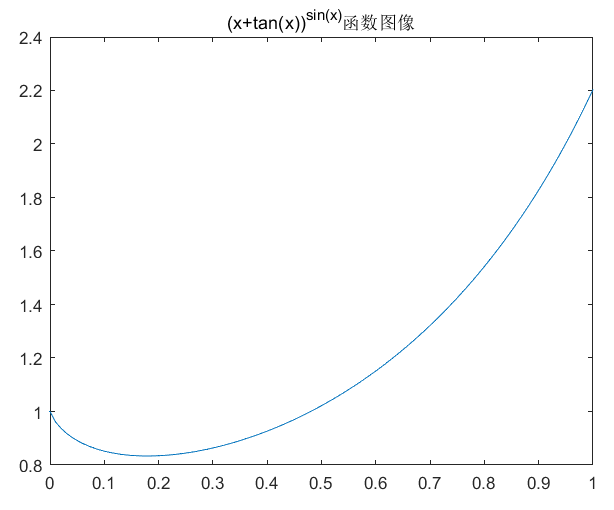
x=0:0.01:1;
y=(x+tan(x)).^sin(x);
plot(x,y)
title('(x+tan(x))^{sin(x)}函数图像')
函数图像
2.嵌套函数
2.1.嵌套函数的定义与分类
嵌套函数nested-function
嵌套函数的优点
-
可以方便解决变量共享问题;
-
复杂的表达式中涉及的参数传递;
-
编写GUI(图形用户界面)时,参数传递问题。
嵌套在函数体内部的函数,嵌套函数可以方便的实现变量共享,可以出现在函数体内部任意位置,除if/else,while,switch等结构语句中。嵌套函数在尾末必须加上end。
例1:嵌套函数简单应用(内外变量共享)
function r = MyTestNestedFun(input) a = 5; c = sin(input)+tan(input); function y = nestedfun(b) y = a*c+b; end r = nestedfun(5); end
例2:嵌套函数的变量作用域(内部调用外部)
function r = NestedFunctionVarScopeDemo(a) b = a+1;function Nested1c = b+1;function Nested11d = c+a;endNested11;end Nested1
例3:嵌套函数的变量作用域2(未调用时不运行)
function r = NestedFunctionVarScopeDemo2(a) b = a+1;function Nested1c = b+1function Nested11d = c+a;endend Nested1 e = c1 r = d; end
例4:嵌套函数的变量作用域3(无嵌套关系,不能共享)
function r = NestedFunctionVarScopeDemo3(a) b = a+1;function Nested1c = b+1;c1 = 10;Nested2;c2 = d^2; %这一步有问题end Nested1 r = c2 end
2.2.嵌套函数彼此调用关系
例5:父函数与子函数(父调用子,不能调用孙)
function r = NestedFunctionCallDemo1(a) b = a+1;function c1 = Nested1(x)c = b+1;c1 = 10+c*x;function d = Nested11d = c+a;endend c1 = Nested1(1); r = Nested11; end
例6:父函数与子函数(子调用父,孙调用爷)
function NestedFunctionCallDemo2(flag)
switch flagcase 1disp('flag = 1')return;case 2disp('flag = 2')return;case 3disp('flag = 3')returnotherwisedisp(['flag = ', num2str(flag)]);returnend
function NestedFunctionCallDemo2(flag)% 续function NestedFun1NestedFunctionCallDemo2(1);%子调用父;NestedFun2function NestedFun2NestedFunctionCallDemo2(3);%孙调用爷;endend
end
例7:父函数与子函数(子调用叔父)
function NestedFunctionCallDemo3 Nested1(5)function Nested1(x)disp(['Nested1执行,输入:', num2str(x)])Nested2(6)function Nested11(xx)disp(['Nested11执行,输入:',num2str(xx)]);endendfunction Nested2(y)disp(['Nested2执行,输入:',num2str(y)])function Nested22(yy)disp(['Nested22执行,输入:',num2str(yy)]);endend end
例8:父函数与子函数(孙调用大爷,不能用堂伯堂哥)
function NestedFunctionCallDemo4 Nested1(5)function Nested1(x)disp(['Nested1执行,输入:', num2str(x)])Nested11(6)function Nested11(xx)disp(['Nested11执行,输入:',num2str(xx)]);Nested2(pi)Nested22(10);endendfunction Nested2(y)disp(['Nested2执行,输入:', num2str(y)])Nested22(pi*pi)function Nested22(yy)disp(['Nested22执行,输入:',num2str(yy)]);endend end
父函数与子函数:
嵌套:父亲,儿子,孙子
不同嵌套:亲属关系
父子互助,不能求孙
子可求父、伯、大爷、爷,不能求侄儿
2.3.嵌套函数在积分和微分中应用
例1:求积分,已知a,e和l,求\beta_0?

function sol = example541(a,e,l)function fun(beta)f =a.*(1-e.^2)./(1-e.^2.*sin(beta).^2).^(3/2);endfunction g = fun(beta0)g = quadl(@fun1,0,beta0)-1;endsol = fzero(@fun2,3); end sol = example541(20,0.6,6)
例2:
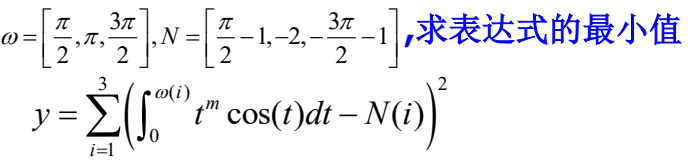
function m = Findm w = [pi/2, pi, pi*1.5] N = [pi/2-1, -2, -1.5*pi-1]; function y = ObjecFun(m)y = (quadl(@(t) t.^m.*cos(t), 0, w(1))^2 + (quadl(@(t).^m.*cos(t), 0, w(2))^2 + (quadl(@(t).^m.*cos(t), 0, w(3))^2; end m = fminbnd(@ObjecFun, 0, 2); end % 第二段代码 function m = Findm w = [pi/2, pi, pi*1.5]; N = [pi/2-1, -2, -1.5*pi-1]; function y = ObjecFun(m) s = @(w)arrayfun(@(ww) quadl(@(t) t.^m.*cos(t), t, ww), w); y = sum((s(w)-N).^2); end m = fminbnd(@ ObjecFun, 0, 2); end
例3:求微分方程在[0, 5]范围的解,a为参数
![]()
function example545(a)
tspan = [0,5]; % 变量求解区间
y0 = [1,0]; % 初值
[t,y] = ode45(@tfys, tspan, y0); % 调用ode45求解方程
figure;
plot(t, y(:,1),'k'); %画函数y(t)的曲线
hold on;
plot(t,(:,2), 'k:'); %画函数y(t)导数的曲线
set(gca,'fontsize',12); % 设置当前坐标轴字体大小
xlabel('\itt','fontsize',16); %标注x轴
ylabel('\ity','fontsize',16); %标注y轴
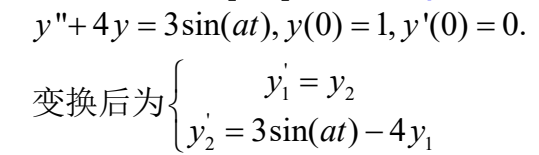
function example545(a) %嵌套函数定义微分方程组function dy = tfys(t,y)dy(1,1) = y(2); %对应于例子中方程组第一个方程dy(2,1) = 3*sin(a*t)-4*y(1);%对应于例子中方程组第二个方程end end
3.微分和积分
敬请期待
4.蒙特卡洛法
4.1.圆周率的模拟
例1:蒲丰投针问题
18世纪,蒲丰提出以下问题:设我们有一个以平行且等距木纹铺成的地板(如图),现在随意抛一支长度比木纹之间距离 小的针,求针和其中一条木纹相交的概率。并以此概率,布丰提出的一种计算圆周率的方法——随机投针法。这就是蒲丰投针问题(又译“布丰投针问题”)
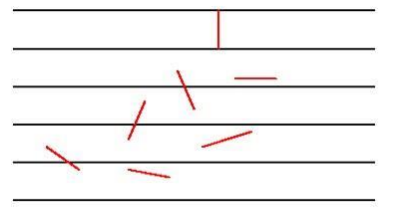
证明:由于向桌面投针是随机的,所以用二维随机变量(X,Y)来确定它在桌上的具体位置。设X表示针的中点到平行线的的距离,Y表示针与平行线的夹角,如果x<l/2sin(y)时,针与直线相交。
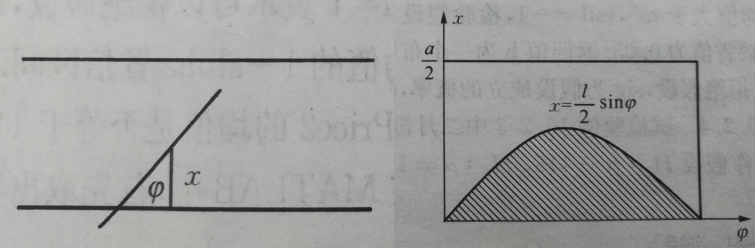
并且X在服从均匀分布,Y在服从均匀分布,XY相互独立,由此可以写出(X,Y)的概率密度函数
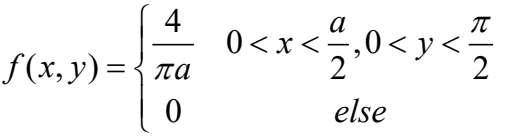
因此所求概率
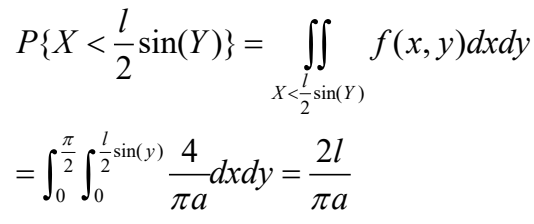
Monte Carlo方法是计算机模拟的基础,它的名字来源于世界著名的赌城——摩纳哥的蒙特卡洛, 其历史起源于 1777 年法国科学家蒲丰提出的一种计算圆周π 的方法——随机投针法,即著名的蒲丰投针问题。
Monte Carlo方法的基本思想是首先建立一个概率模型,使所求问题的解正好是该模型的参数或其他有关的特征量. 然后通过模拟一统计试验, 即多次随机抽样试验 (确定 m和 n) ,统计出某事件发生的百分比。只要试验次数很大,该百分比便近似于事件发生的概率.这实际上就是概率的统计定义。利用建立的概率模型,求出要估计的参数。蒙特卡洛方法属于试验数学的一个分支。
MATLAB语言编程实现:1)
l = 1; a = 2;n = 10000;m = 0; for k = l : n x = unifrnd(0, a/2); y = unifrnd(0, pi/2);if x < l/2*sin(y)m=m+1;end end p=m/n;pi_m=1/p pi_m=3.2584
2)
l=1;a=2;n=10000;m=0; x=unifrnd(0,a/2,1,n); y=unifrnd(0,pi/2,1,n); [gs,wz]=find(x<l/2*sin(y)); m=sum(gs); p=m/n;pi_m=1/p pi_m=3.1636
4.2.计算N重积分(均匀分布)
原理:用蒙特卡洛法计算N重积分积分:设D为n维空间Rn的一个区域,f(x)∈D Rn→R,区域D上的n 重积分用下式表示:
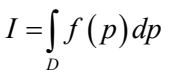
可以认为 I=(区域D的测度) X (函数f的期望)。基本的蒙特卡洛法就是找一个超立方体(测度已知,为Mc)包含区域D,在D内随机生成n(n一般足够大)个均匀分布的点,统计落入区域D的点,假设有m个。
则区域D的测度
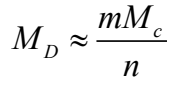
函数f的期望
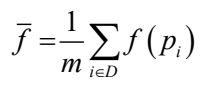
积分为

例1:用蒙特卡洛法计算积分
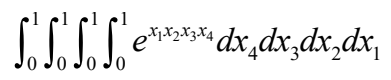
%构造被积函数,x为长为4的列向量或者矩阵(行数为4)。x的每一列表示4维空间中的一个点 f = @(x) exp(prod(x)); n = 10000; X = rand(4,n); % 随机生成n个4维单位超立方体内的点 I = sum(f(x))/n % 用基本的蒙特卡洛法估计积分值 I =1.069245225746442
例2:用蒙特卡洛法计算积分
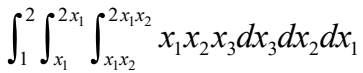
f = @(x) prod(x);n = 100000;% 随机均匀积分区域的点 x1 = unifrnd(1,2,1,n);x2 = unifrnd(1,4,1,n); x3 = unifrnd(1,16,1,n); ind = (x2>=x1)&(x2<=2*x1)&(x3<=2*x1.*x2)&(x3>=x1.*x2); % 积分区间 X = [x1;x2;x3]; I = (4-1)*(16-1)*sum(f(X(:,ind)))/n I = 1.791951576008592e+02
4.3.计算N重积分(等序列分布)
在区间[a,b]中的一个(确定性)点列x1,x2,... ,若对所有的有界黎曼(Riemann)可积函数f(x),均有
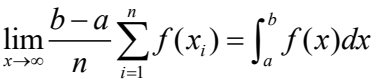
则称该点列在[a,b]中是等分布的。令(ξ)表示ξ的小数部分,即(ξ)=ξ一[ξ],这里[ξ]表示不超过ξ的最大整数。
定理6.1 若θ为一个无理数 ,则数列为xn= (nθ), n =1,2 ,... ,在[0,1]中是等分布的。
对于一般的区间[a,b],可以令un=xn (b-a)+a来得到[a,b]中等分布的点列。对于s重积分,一般是挑选s 个对有理数线性对立的无理数,来得到包含积分区域D的超长方体内的均匀分布的点列。[uai, ubi ],…得到用等分布序列蒙特卡洛法计算的积分的近似值:
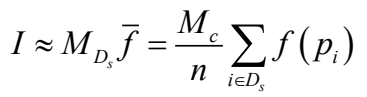
例3:用等序列蒙特卡洛法计算例1的积分
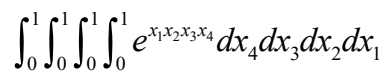
f = @(x) exp(prod(x)); n = 10000; % 选取对有理数独立的无理数sqrt(2),sqrt(3),sqrt(6)/3,sqrt(10)来分成等分布序列 x = bsxfun(@times, repmat(1:n,4,1),[sqrt(2);sqrt(3);sqrt(6)/3;sqrt(10)]); x = mod(x,1);%对1取余运算,即得小数部分 I = sum(f(x))/n % I = 1.069297245824625
例4:用等序列蒙特卡罗法计算积分

包含积分区域的超长方体:
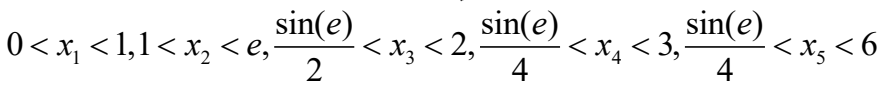
选取对有理数独立的无理数

来生成等分布序列,matlab程序为:
f = @(x) sin(x(1,:).*exp(x(2,:).*sqrt(x(3,:))))+x(4,:).*x(5,:); n = 10000000; x = bsxfun(@times,repmat(1:n.5,1),[sqrt(2);sqrt(3);sqrt(6)/3;sqrt(10);sqrt(19)]); x = mod(x,1); % 一下变换,使得区间(0,1)上的等分布序列变到各层积分区间上去 BminusA = diff([0.5 sin(exp(1))/2 sin(exp(1))/4]) x(2:end,:) = bsxfun(@times,x(2:end,:),BminusA);