目录

1.判断一个表是否是环形链表！

代码如下

解析如下

2.快指针的步数和慢指针的步数有什么影响（无图解析）

3.怎么找到环形链表的入环点

代码如下

解析如下

---

1.判断一个表是否是环形链表！

代码如下

bool hasCycle(struct ListNode *head) {struct ListNode* fast = head;struct ListNode* slow = head;while(fast && fast->next){fast = fast->next->next;slow = slow->next;if(fast == slow){return true;}}return false;
}

解析如下

 快慢指针就是一个指针一次走好几个节点，而一个指针一次走少一点。字面意思

这里采用的是一个走两节点，一个走一个节点。

为什么要用快慢指针呢？

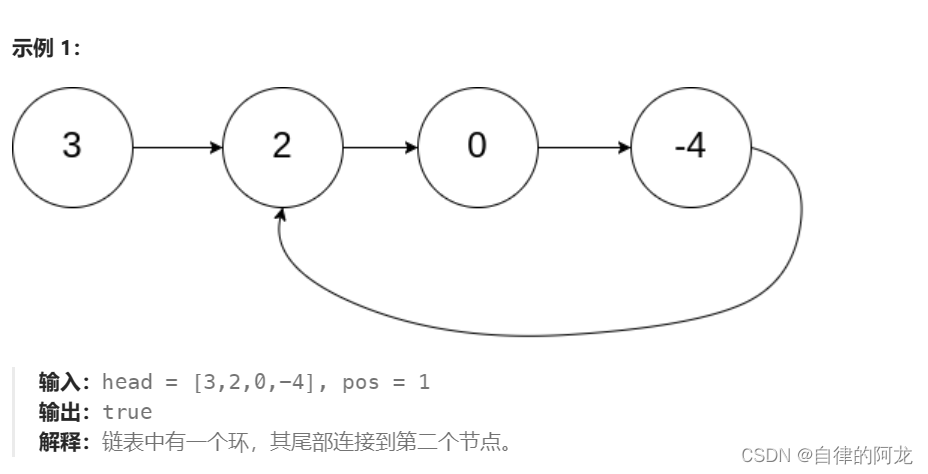
这个图是本题的原图，你可以用一个手指当做快指针，一个手指当做慢指针 。最终两个手指会相遇。这就是最普遍的快慢指针，fast走的是slow的路程的两倍，这就是相当于一个追击问题，再跑1000米的时候，你的好朋友的配速是你的两倍，最终他会超你一圈一个道理。

2.快指针的步数和慢指针的步数有什么影响（无图解析）

根据上面的判断，那这两个指针一定会相遇吗？

思考如果快指针一次走三，慢指针一次走一，那他们两还会相遇吗？

如果快指针走N慢指针走M呢？

 其实上面第一题 一个走两步一个走一步的方法是有一个公式的。

就以这个为例，当slow走到2的时候，fast已经走到-4，那他两距离相差1，下一次fast和slow必定相遇，因为两人每次走的距离差为1，把slow入环时两者的距离记作N，因为两者的距离差为1，N-1-1-1-1-1......N总有被减到0的时候，减到0那两者就是在一个位置，就相遇了。

那如果一个走三步的情况和一个走一步的情况呢？

这个也很好解释，假设在slow进入环的时候，fast和slow的距离为N，头结点到slow的距离为L，环的大小为C

 如果一个走三步一个走一步那两者的每次的距离差就是2.现在要让fast去追这个slow。

两者差距为N。如果每次都减2，如果N为偶数的话，那还好最终会减到0,

如果N为奇数的话最终（除了1）最终可能会减为-1，就是fast 直接超过 slow。

那最后会不会相遇呢？现在两者的距离就变成C-1了，如果C-1为偶数那接下来两个人就会碰到，

如果为奇数，那就不行了两人会再次错过吗？其实不然

 假设slow 进环时总的距离是L，期间fast就走了L+n * C - N（小n是fast走的圈数，随机值）

因为fast最终走的距离是slow 的三倍，最终可以列出等式 3L = L + n * C - N

最终 2L = n * c - N . 因为两者不相遇是因为 N 为奇数，所以N为奇数 ，2L一定是偶数。

那n * c 总的来说也必须是一个奇数，因为等式一个奇数减偶数才能等于一个偶数。

所以 c 是奇数 ，c -1 就是偶数。那说明两者不会一直不相等。最终可能会相遇。

3.怎么找到环形链表的入环点

代码如下

struct ListNode *detectCycle(struct ListNode *head) {struct ListNode* fast = head,*slow = head;while(fast && fast->next){fast = fast->next->next;slow = slow->next;if(fast == slow){struct ListNode* cur = slow;while(cur != head){cur = cur->next;head = head->next;}return head;}}return NULL;}

解析如下

首先做这题前，我们需要画一个图

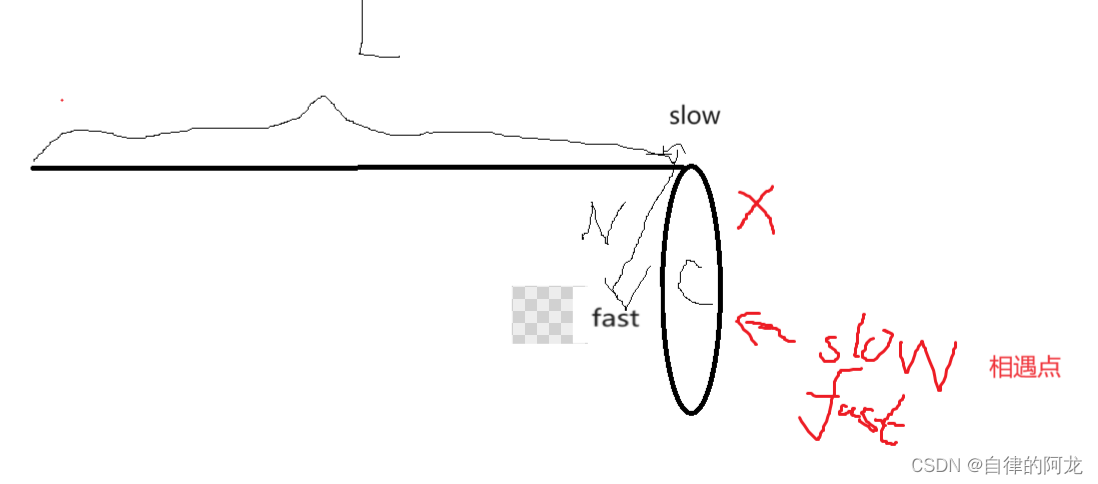
 同样假设入环点到头结点的距离为L，两者相遇的距离为X，环的大小为C

首先在slow 在入环点的时候，fast 走了 L + C * n - N 。

在slow 入环后 两者在 X 距离后相遇。

之后slow 所走的路程就变为了 L + X，fast 走的路程就是 L + n * C + X。

因为fast的路程等于slow 的两倍，所以就可以列出等式，2*（L+X） =  L + n * C + X.

解出答案后等于 L = n * C - X。这个答案的意义是什么呢？

就是L的距离等于这么fast走的这么多圈后减掉 X的距离。就是L 加上 slow 多走的环的距离，就是 fast 之前走过多少圈的环。那接下来就可以知道，其实我们可以用头指针（头结点）和慢指针的位置，每人都每次都向后走一步，最后两者就会在入环点相遇。

因为L = n * C - X，所以只要让两者相遇的点作为起点，然后向后走n 圈后，就等于L ，所以一个指针从头开始走，一个指针从 相遇点开始走，两者最终会在相遇点L 相遇。