微信公众号上线,搜索公众号小灰灰的FPGA,关注可获取相关源码,定期更新有关FPGA的项目以及开源项目源码,包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等

1、循环码原理
循环码(cycle code),是一种线性分组码。具有线性码的一般性质外,还具有循环性。
循环性是指任一码组循环一位以后,仍然为该码中的一个码组。
即将最右端的一个码元移至左端,或者将最左端的一个码元移至右端,仍然为该码中的一个码组。
一个循环码的例子
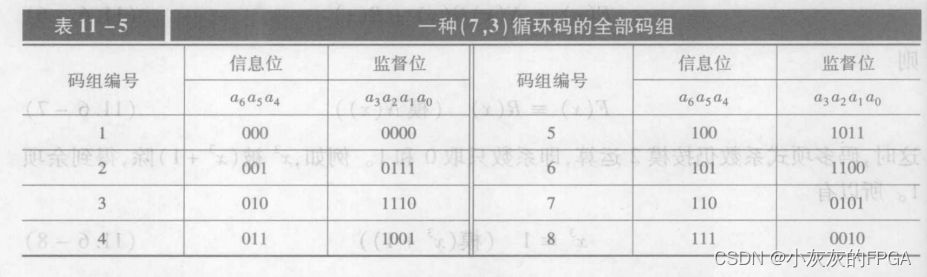
长度n的循环码组的多项式
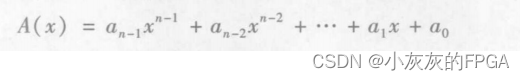
(2)循环码的运算
①码多项式的按模运算
模n(modulo-n)运算
若一个整数(integer)m,满足
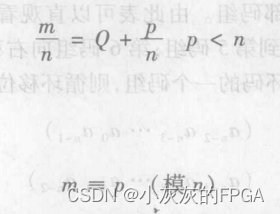
Q为整数
在模n运算下,一个整数m等于它被n除得的余数(remainder)。
码多项式的按模运算,若任一多项式F(x)被一n次多项式N(x)除,得到商式(quotient)Q(x)和一个次数小于n的余式(residue)R(x)
注意:模2运算中,用加法代替了减法

一个重要结论:一个长为n的循环码必定为按模(x^n+1)运算的一个余式
②循环码的生成矩阵G
在循环码中,一个(n,k)码有2^k个不同码组。
g(x)必须是一个常数项不为“0”的(n-k)次多项式,而且这个g(x)还是(n,k)码中次数为(n-k)的唯一一个多项式。
以唯一的(n-k)次多项式g(x)为码生成多项式
可得到循环码的生成矩阵G

③任一(n,k)循环码的生成多项式
任一循环码多项式A(x)都是g(x)的倍式,即A(x)=h(x)×g(x)
生成多项式g(x)是一个(n-k)次多项式
x^k×g(x)是一个n次多项式
进行模(x^n+1)运算可得
(xk×g(x))/(xn+1) = Q(x)+A(x)/(x^n+1)
左端分子和分母都是n次多项式,故Q(x)=1
(xk×g(x))=(xn+1)+h(x)×g(x)
(xn+1)=g(x)×(xk+h(x))
生成多项式g(x)应该是(x^n+1)因子中的一个(n-k)次多项式
④循环码的编码方法
在编码时,根据给定的(n,k)值选定生成多项式g(x),即从(x^n+1)的因子中选一个(n-k)次多项式作为g(x)
具体编码规则:
设m(x)为信息码多项式,其次数小于k
x^(n-k)×m(x)的次数必定小于n,即在信息码后面附加上(n-k)个“0”
余式r(x)=g(x)/(x^(n-k)×m(x)),次数必定小于g(x)的次数(n-k)
余式r(x)与x^(n-k)×m(x)相加,得到码多项式
一个以(7,3)码为例分析:
第一步:
信息码为110,m(x)=x ^ 2+x
n=7,k=3,n-k=4
x ^ (n-k)×m(x)=x ^ 4×(x ^ 2+x)=x ^ 6+x ^ 5,即1100000
第二步:
x ^ n+1=x ^ 7+1=(x+1)×(x ^ 3+x ^ 2+1)×(x ^ 3+x+1)
循环码的生成多项式g(x)有两个:
(x+1)×(x ^ 3+x ^ 2+1)=x ^ 4+x ^ 2+x+1
(x+1)×(x ^ 3+x+1)=x ^ 4+x ^ 3+x ^ 2+1
用g(x)除x^(n-k)×m(x),得到商Q(x)和余式r(x)
(x ^ 6+x ^ 5)/(x ^ 4+x^ 2+x+1)=(x ^ 2+x+1)+(x ^ 2+1)/(x ^ 4+x ^ 2+x+1)
即Q(x)=(x2+x+1);r(x)=(x2+1)
第三步:
编码为:A(x)=x^(n-k)×m(x)+r(x)=1100000+101=1100101
⑤循环码的解码方法
接收端解码有两个要求:检错和纠错
通过余项是否为零来判断接收码组中有无错码
传输过程中为发送错误时,接收码组B(x)与发送码组A(x)相同,即B(x)必定能被g(x)整除;
传输过程中发生错误时,B(x)被g(x)除时,可能存在除不尽而有余项;
B(x)/g(x)=Q(x)+r(x)/g(x)
检错解码器的原理,一个除法电路和缓冲移位寄存器
除法电路与发送端编码器的除法电路相同,进行B(x)/g(x)的运算
余项为“0”,将暂存于缓冲器中的接收码组发送到解码器的输出端
余项不为“0”,将缓存器中的接收码组删除,并向发送端发出一个重发指令,要求重发一次该码组
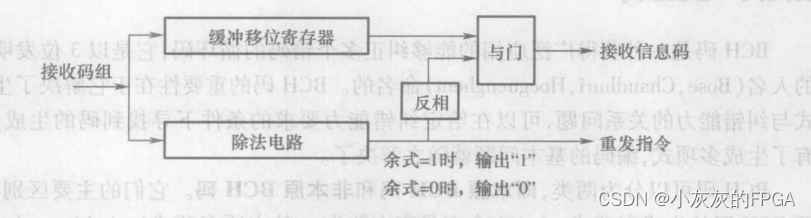
捕错解码法,具体解码规则:
第一步:
用生成多项式g(x)除接收码组B(x),得出余式r(x)
第二步:
按余式r(x),用查表法或其他计算获得错误图样E(x),确定错码的位置
第三步:
从B(x)中减去E(x),得到已经纠正错码的原发送码组A(x)
通信原理板块——线性分组码之循环码
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.rhkb.cn/news/189890.html
如若内容造成侵权/违法违规/事实不符,请联系长河编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
C++17中std::optional的使用
模版类std::optional管理一个可选的(optional)存储值(contained value),即可能存在也可能不存在的值。std::optional的一个常见用例是存储可能失败的函数的返回值。与其它方法相反(例如std::pair<T, bool>),std::optional可以很好地处理构造成本高昂的对象&am…
在GORM中使用并发
一个全面的指南,如何安全地使用GORM和Goroutines进行并发数据处理
效率是现代应用程序开发的基石,而并发在实现效率方面发挥着重要作用。GORM,这个强大的Go对象关系映射库,使开发人员能够通过Goroutines embrace并行性。在本指南…
Go,14周年[译]
国内的双十一购物狂欢已没有了当年的那种热闹与喧嚣,但大洋彼岸的Go团队却始终保持稳中有增的开发和语言演进节奏。今晨Go核心团队的Russ Cox[1]代表Go语言项目团队在Go官博上发表了《Fourteen Years of Go》[2]的博文,纪念Go语言开源14周年[3]ÿ…
【数据结构与算法】JavaScript实现单向链表
文章目录 一、单向链表简介二、封装单向链表类2.0.创建单向链表类2.1.append(element)2.2.toString()2.3.insert(position,element)2.4.get(position)2.5.indexOf(element)2.6.update(position,element)2.7.removeAt(position)2.8.其他方法2.9.完整实现 一、单向链表简介
链表…
C语言——个位数为 6 且能被 3 整除但不能被 5 整除的三位自然数共有多少个,分别是哪些?
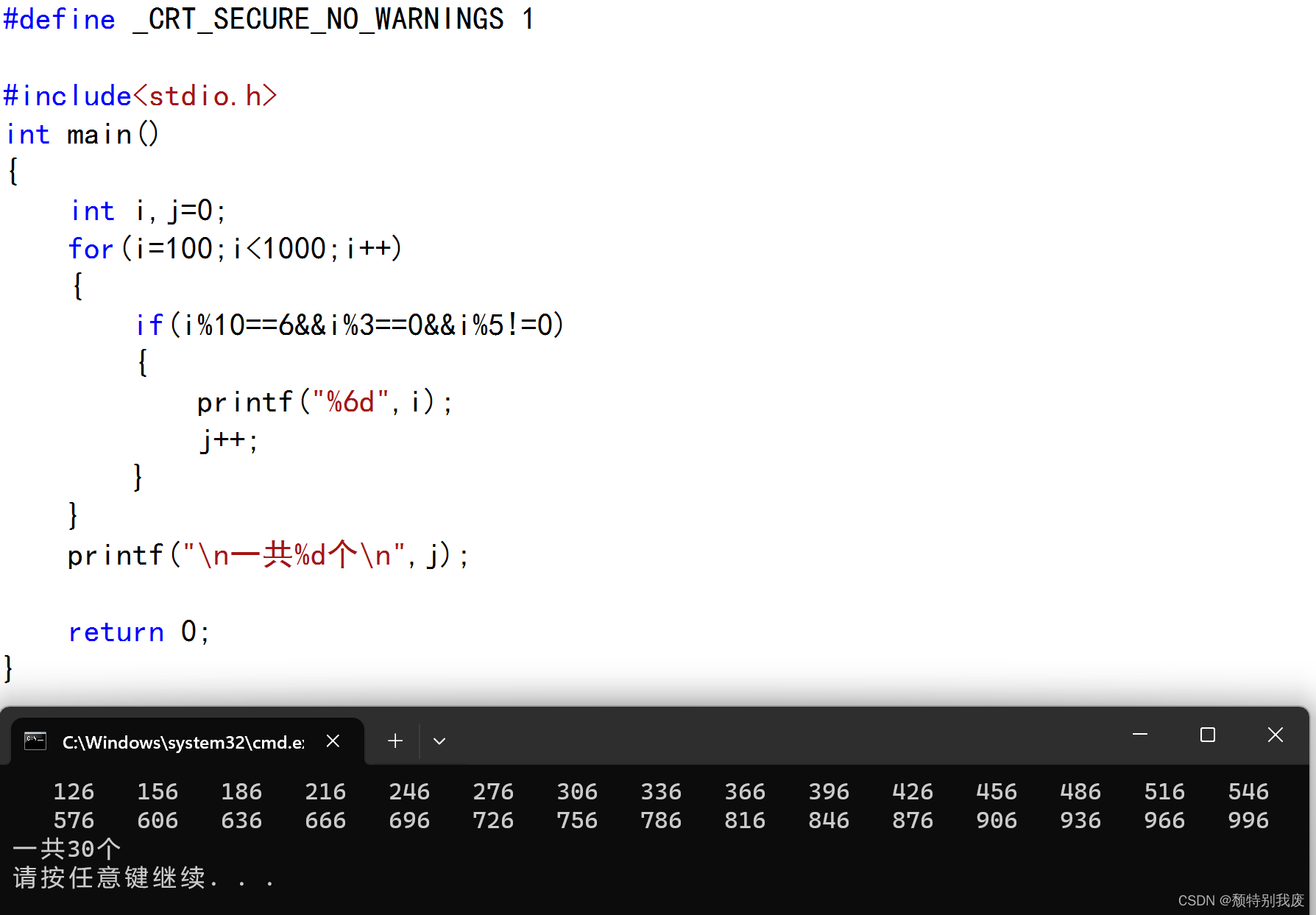
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>
int main()
{int i,j0;for(i100;i<1000;i) {if(i%106&&i%30&&i%5!0){printf("%6d",i); j;}}printf("\n一共%d个\n",j);return 0;
}
%6d起到美化输出格式的作用ÿ…
C语言基础篇4:变量与存储
1 局部变量和全局变量 在介绍局部变量和全局变量前,先了解一些关于作用域方面的内容。作用域的作用就是决定程序中的哪些语句是可用的,换句话说,就是程序中的可见性。作用域有局部作用域和全局作用域,那么局部变量就具有局部作用域…
代码随想录算法训练营第四十九天丨 动态规划part12
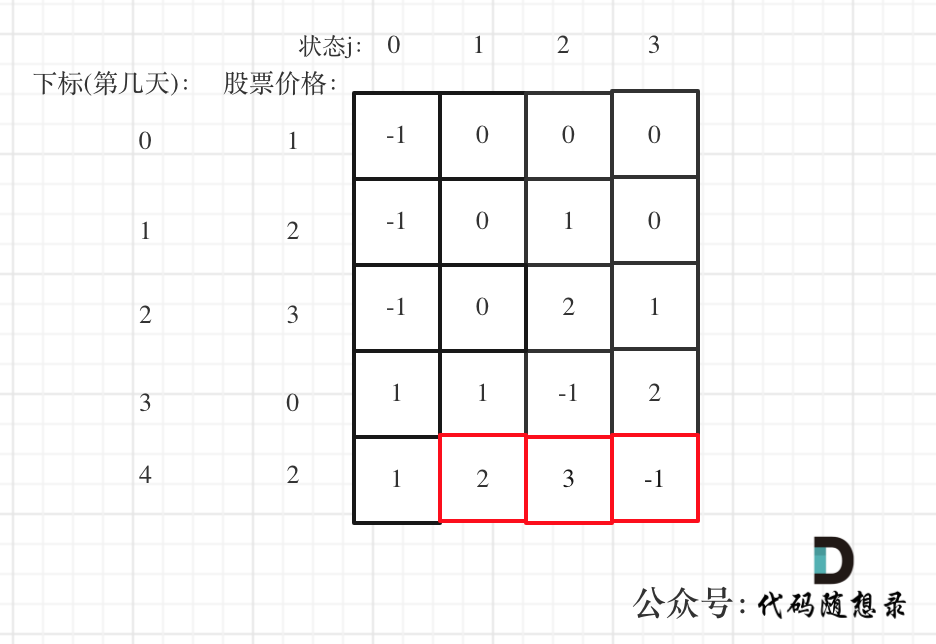
309.最佳买卖股票时机含冷冻期
思路
相对于动态规划:122.买卖股票的最佳时机II (opens new window),本题加上了一个冷冻期
在动态规划:122.买卖股票的最佳时机II (opens new window)中有两个状态,持有股票后的最多现金…
NSS [HUBUCTF 2022 新生赛]checkin
NSS [HUBUCTF 2022 新生赛]checkin 判断条件是if ($data_unserialize[username]$username&&$data_unserialize[password]$password),满足则给我们flag。正常思路来说,我们要使序列化传入的username和password等于代码中的两个同名变量࿰…
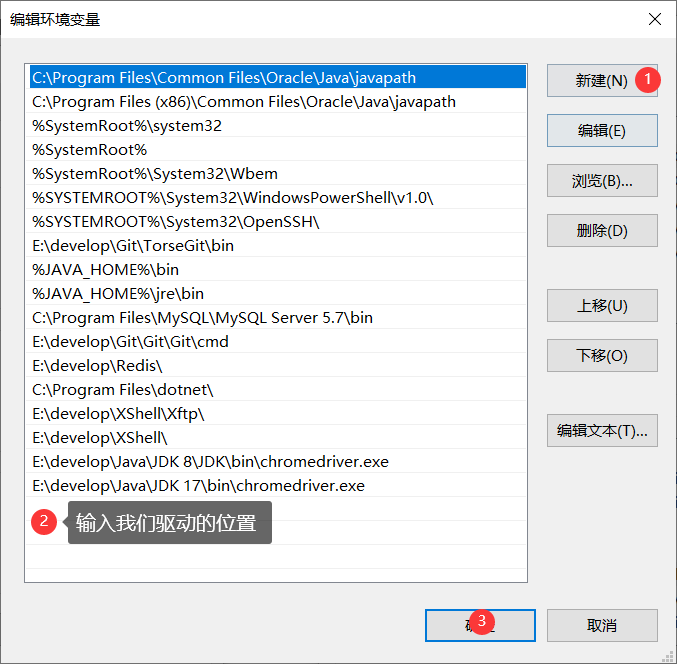
番外 1 : Java 环境下的 selenium 搭建
Java 环境下的 selenium 搭建 一 . 下载谷歌浏览器二 . 下载谷歌浏览器驱动2.1 查看谷歌浏览器版本2.2 下载对应版本的谷歌驱动2.3 解压下载好的驱动压缩包 , 将下载好的 chromedriver.exe 放到java 系统环境变量下 三 . 下载 Edge 浏览器的驱动3.1 查看 Edge 浏览器的版本3.2 …
k8s的Init Containers容器实现代码版本升级发布和deployment版本回退:实战操作版
Pod中的初始化容器:Init Containers
initContainers实现理论前提:同一个Pod内的容器共享 网络、volume等资源
Init Containers
在Kubernetes中,init容器是在同一个Pod中的其他容器之前启动和执行的容器。它的目的是为Pod上托管的主应用程序执行初始化…
洛谷P9388 [THUPC 2023 决赛] 先人类的人类选别(主席树+权值线段树)
题目 思路来源
P9388 [THUPC 2023 决赛] 先人类的人类选别 - 违规用户名FkZyA0!2 的博客 - 洛谷博客
题解
这个题是2023ccpc深圳热身赛的题目,也是thupc2023决赛的题目,
学弟问了一下,于是就乱搞了一下,搞了很久才a࿰…
Linux ____03、文件类型、属性、修改文件属性(更改文件权限)(命令)
文件类型、属性、修改文件属性 一、文件类型二、文件属性三、修改文件属性1、chgrp:更改文件属组2、chown:更改文件属主,也可以同时更改文件属组3、chmod:更改文件9个属性————————如觉不错,随手点赞ÿ…
微信小程序真机调试连接状态一直在正常和未链接之间反复横跳?
背景:小程序真机调试的时候,发现真机的network不显示接口调用情况,控制台也没有输出内容。具体如下所示; 解决方法:
1、确保手机端连接的网络和微信开发者工具网络一致,比如用同一个WiFi
2、真机自动调试…
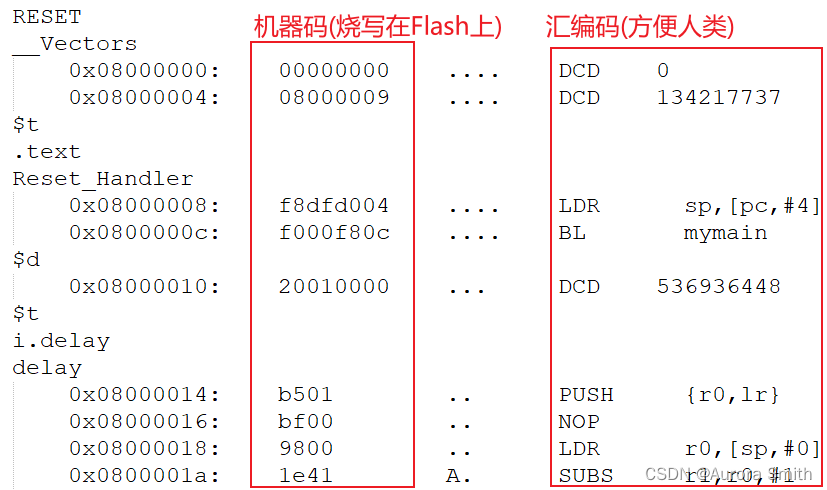
编程知识\_C与汇编深入分析
1. 汇编怎么调用C函数
1.1 直接调用
bl main
1.2 想传参数怎么办?
在arm中有个ATPCS规则(ARM-THUMB procedure call standard(ARM-Thumb过程调用标准)。 约定r0-r15寄存器的用途: r0-r3 调用者和被调用者之间传参数 r4-r11 函…
Flink SQL自定义标量函数(Scalar Function)
使用场景: 标量函数即 UDF,⽤于进⼀条数据出⼀条数据的场景。
开发流程:
实现 org.apache.flink.table.functions.ScalarFunction 接⼝实现⼀个或者多个⾃定义的 eval 函数,名称必须叫做 eval,eval ⽅法签名必须是 p…
springboot rocketmq 延时消息、延迟消息
rocketmq也有延迟消息,经典的应用场景:订单30分钟未支付,则取消的场景 其他博客提到从rocketmq5.0开始,支持自定义延迟时间,4.x只支持预定义延迟时间,安装rocketmq可参考RocketMq简介及安装、docker安装ro…
⑤ 【MySQL】DCL语句 —— 用户管理、权限控制
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ MySQL用户与权限 ⑤ 【MySQL】DCL语句 —— 用…
推荐文章
- # 从浅入深 学习 SpringCloud 微服务架构(八)Sentinel(1)
- #if等命令的学习
- #华为推送# 电商应用如何提高用户购买率?推送服务助您一臂之力,现在接入更有专人为您解决技术问题
- (15)线程的实例认识:同步,异步,并发,并发回调,事件,异步线程,UI线程
- (BERT蒸馏)TinyBERT: Distilling BERT for Natural Language Understanding
- (动手学习深度学习)第13章 实战kaggle竞赛:狗的品种识别
- (二)结构型模式:7、享元模式(Flyweight Pattern)(C++实例)
- (数学) 剑指 Offer 62. 圆圈中最后剩下的数字 ——【Leetcode每日一题】
- (四) ClickHouse 中使用 `MaterializedMySQL` 引擎单独同步 MySQL 数据库中的特定表(例如 `aaa` 和 `bbb`)
- (搜索) 剑指 Offer 12. 矩阵中的路径 ——【Leetcode每日一题】
- (微信开发)Laya转发H5网页到微信,带图片
- (一)面试需要掌握的技巧

![Go,14周年[译]](https://img-blog.csdnimg.cn/img_convert/42a0b2818053eb95dedb1b1b9cee78c1.jpeg)



![NSS [HUBUCTF 2022 新生赛]checkin](https://img-blog.csdnimg.cn/img_convert/80531a438bc9d8641c0339a895eafed2.png)
![洛谷P9388 [THUPC 2023 决赛] 先人类的人类选别(主席树+权值线段树)](https://img-blog.csdnimg.cn/4dca2b95235a432f95d2189d571ff9c4.jpeg)