1.问题建模

导入库

import numpy as np
import pandas as pd
from sklearn.model_selection import KFold
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import OneHotEncoder
import lightgbm as lgbfrom matplotlib import colors 
from matplotlib.ticker import PercentFormatter 
import matplotlib.pyplot as plt
import time
import warnings
warnings.filterwarnings('ignore')#设置忽略警告信息，以防止警告信息干扰代码运行。

导入数据集（包括训练数据集和测试数据集）

train = pd.read_csv('train.csv')
test = pd.read_csv('test.csv')

对训练集数据进行描述性统计分析

train.describe()

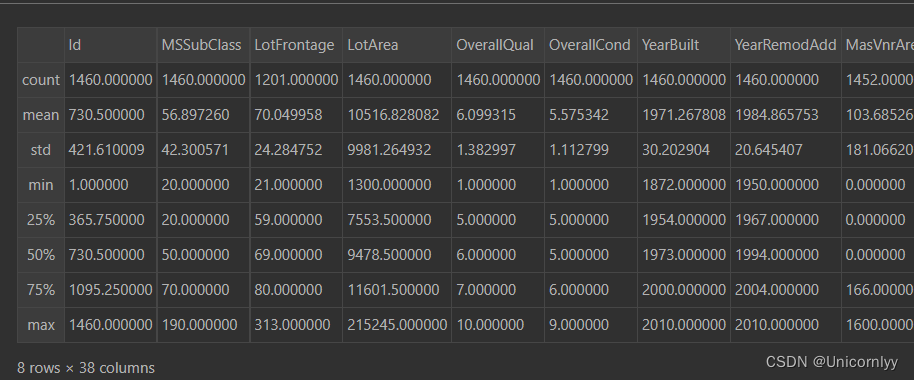
如上图可以查看其百分比、最大最小值、均值标准差以及数量统计~

数据预处理

all_data = pd.concat((train,test))#合并训练集和测试集
all_data = pd.get_dummies(all_data)#进行独热编码
# 填充缺失值
all_data = all_data.fillna(all_data.mean())#使用均值填充缺失值
# 数据切分，将全部数据切分成训练集和测试集
X_train = all_data[:train.shape[0]]
X_test = all_data[train.shape[0]:]
y = train.SalePrice#将训练集中的目标变量（房屋销售价格）提取出来，存储在变量 y 中

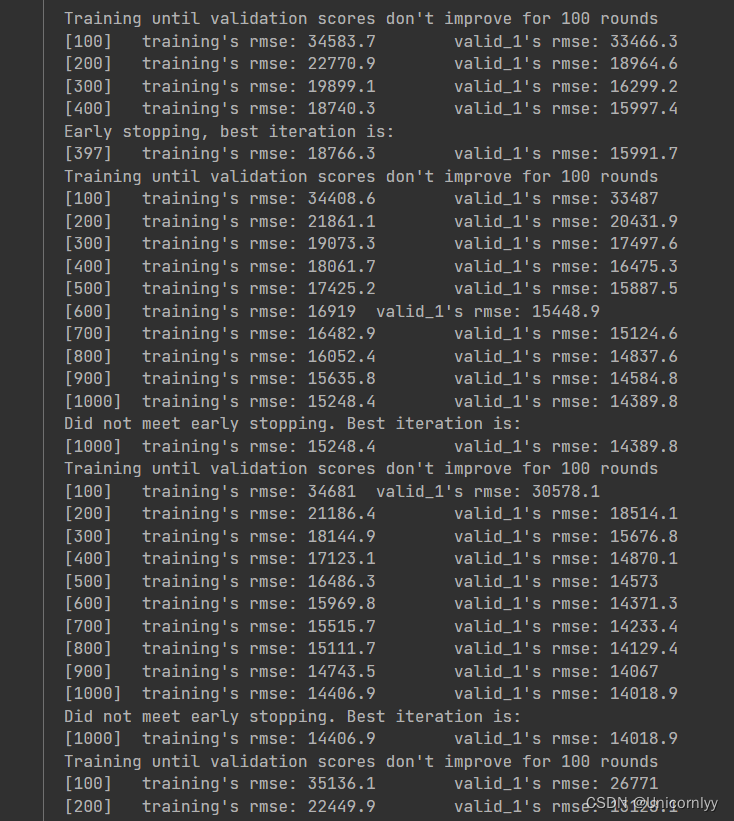
使用 LightGBM 模型进行训练和交叉验证

#定义模型训练的超参数params = {'num_leaves': 63,#表示每棵树的叶子节点数，这个值越大模型的复杂度越高'min_child_samples': 50,#表示每个叶子节点最少样本数，用于控制过拟合'objective': 'regression',#表示模型的优化目标，这里是回归任务'learning_rate': 0.01,#学习率，控制每次迭代参数更新的幅度'boosting_type': 'gbdt',# 表示模型使用的 boosting 方法，这里是 GBDT（Gradient Boosting Decision Tree）'metric': 'rmse',#评估指标，这里是 RMSE（均方根误差）'verbose': -1,#控制训练过程中的输出信息级别} 
import lightgbm as lgb#导入LightGBM库
folds = KFold(n_splits=5, shuffle=True, random_state=2020)#将数据集分成 5 份，并且打乱顺序以增加随机性，设定了随机种子为 2020
#交叉验证的循环
for trn_idx, val_idx in folds.split(X_train, y):trn_df, trn_label = X_train.iloc[trn_idx, :], y[trn_idx]val_df, val_label = X_train.iloc[val_idx, :], y[val_idx]dtrn = lgb.Dataset(trn_df, label = trn_label)dval = lgb.Dataset(val_df, label = val_label) #dtrn训练集dval测试集bst = lgb.train(params,dtrn, num_boost_round=1000,#最大迭代次数valid_sets=[dtrn, dval],early_stopping_rounds=100,#验证集的指标在连续多少轮迭代中都没有提升时，提前结束训练verbose_eval=100#控制训练过程中的输出信息级别)

这段代码的作用是使用交叉验证的方式训练 LightGBM 回归模型，通过参数调优和交叉验证确保模型的泛化能力和稳定性。

结果分析

模型评估

from sklearn.linear_model import Ridge, RidgeCV, ElasticNet, LassoCV, LassoLarsCV#导入了 Ridge 回归、RidgeCV（带交叉验证的 Ridge 回归）、ElasticNet、LassoCV（带交叉验证的 Lasso 回归）和 LassoLarsCV（基于最小角回归的 Lasso 回归）等线性模型
from sklearn.model_selection import cross_val_score#导入了交叉验证的函数，用于评估模型性能def rmse_cv(model):#定义了一个函数 rmse_cv，用于计算给定模型的交叉验证均方根误差（RMSE）rmse= np.sqrt(-cross_val_score(model, X_train, y, scoring="neg_mean_squared_error", cv = 5))#函数中使用了 cross_val_score 来计算模型在训练数据上的均方根误差return(rmse)#返回计算出的均方根误差值model_ridge = Ridge()#初始化了一个 Ridge 回归模型，准备用于后续的交叉验证评估。

使用不同的 alpha 值（正则化参数）来训练 Ridge 回归模型，并计算每个 alpha 对应的交叉验证均方根误差（RMSE）

alphas = [0.05, 0.1, 0.3, 1, 3, 5, 10, 15, 30, 50, 75]
cv_ridge = [rmse_cv(Ridge(alpha = alpha)).mean() for alpha in alphas]

不同 alpha 值下 Ridge 回归模型交叉验证均方根误差的折线图

cv_ridge = pd.Series(cv_ridge, index = alphas)
cv_ridge.plot(title = "Validation")
plt.xlabel("alpha")
plt.ylabel("rmse")

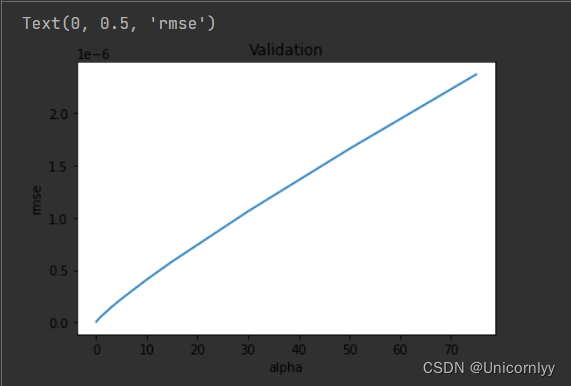
可以直观地展示不同正则化参数对模型性能的影响，有助于选择最佳的 alpha 值。
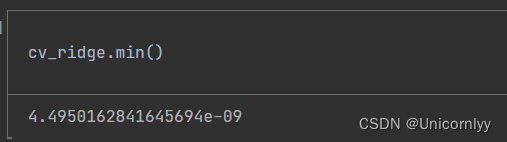
计算 Series 对象 cv_ridge 中的最小值，即交叉验证均方根误差的最小值。

cv_ridge.min()

利用 Lasso 回归模型和交叉验证技术，计算在给定的 alpha 值下，Lasso 回归模型的平均交叉验证均方根误差。这有助于评估模型的预测性能，并在不同的正则化参数下进行模型选择~

model_lasso = LassoCV(alphas = [1, 0.1, 0.001, 0.0005]).fit(X_train, y)
rmse_cv(model_lasso).mean()

利用 Lasso 回归模型的系数信息，统计模型选择了多少个变量，并淘汰了多少个变量

coef = pd.Series(model_lasso.coef_, index = X_train.columns)
print("Lasso picked " + str(sum(coef != 0)) + " variables and eliminated the other " +  str(sum(coef == 0)) + " variables")

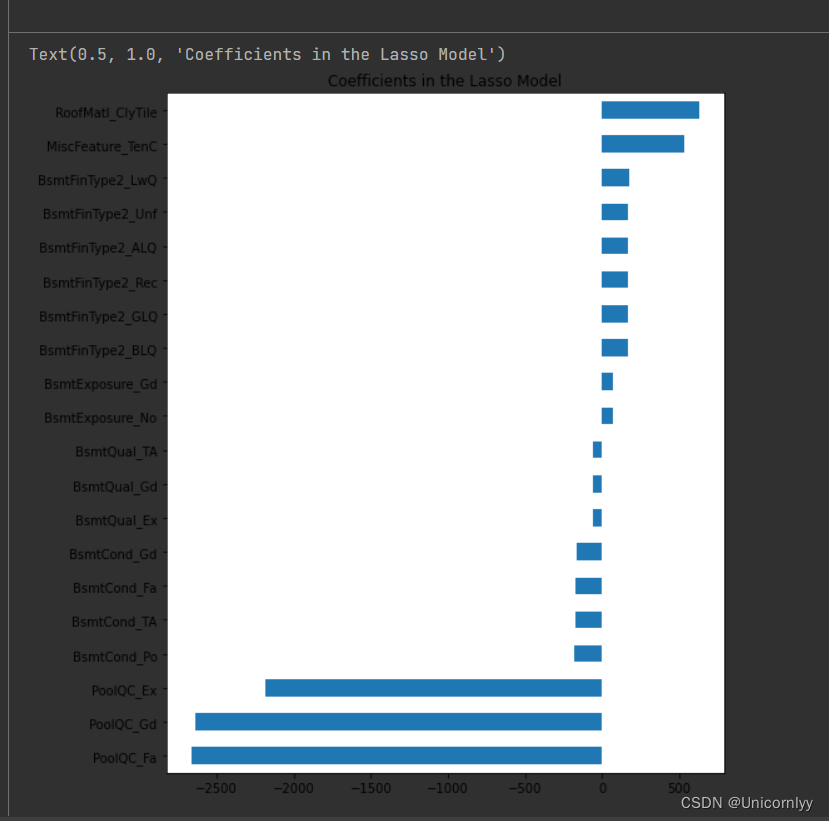
使用 matplotlib 库绘制水平条形图，展示 Lasso 回归模型中具有最高和最低系数数值的变量

import matplotlibimport matplotlib.pyplot as pltimp_coef = pd.concat([coef.sort_values().head(10),coef.sort_values().tail(10)])
matplotlib.rcParams['figure.figsize'] = (8.0, 10.0)
imp_coef.plot(kind = "barh")
plt.title("Coefficients in the Lasso Model")

直观地展示模型对不同变量的重要程度，帮助理解模型对数据的建模方式。

绘制预测值与残差之间的散点图，来观察模型的预测效果以及残差的分布情况

# 接下来观察真实结果与预测结果的残差
matplotlib.rcParams['figure.figsize'] = (6.0, 6.0)preds = pd.DataFrame({"preds":model_lasso.predict(X_train), "true":y})
preds["residuals"] = preds["true"] - preds["preds"]
preds.plot(x = "preds", y = "residuals",kind = "scatter")

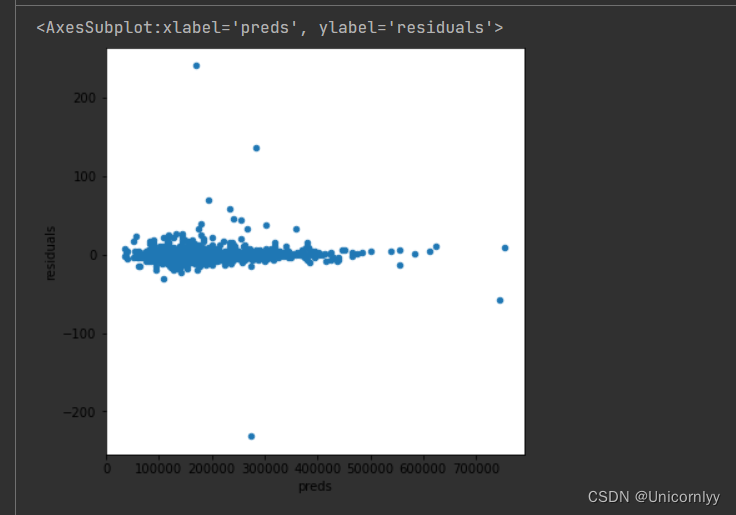
观察散点图的分布情况，可以帮助我们判断模型的预测效果和残差是否符合模型假设~
将之前创建的预测结果 DataFrame preds 与原始训练数据集 train 进行按列拼接，以便将预测结果与原始数据集中的特征和目标值整合在一起。

train = pd.concat([train,preds], axis=1)

利用了 tsfresh 库对时间序列数据进行特征提取

import tsfresh as tsf#该库提供了用于自动时间序列特征提取和选择的功能
import pandas as pd
x = [1,2,4,8]
ts = pd.Series(x)  #数据x假设已经获取
ae = tsf.feature_extraction.feature_calculators.absolute_sum_of_changes(ts)

利用 tsfresh 库对给定的时间序列数据进行绝对变化量特征的计算，最终得到了该特征的数值，并存储在变量 ae 中。
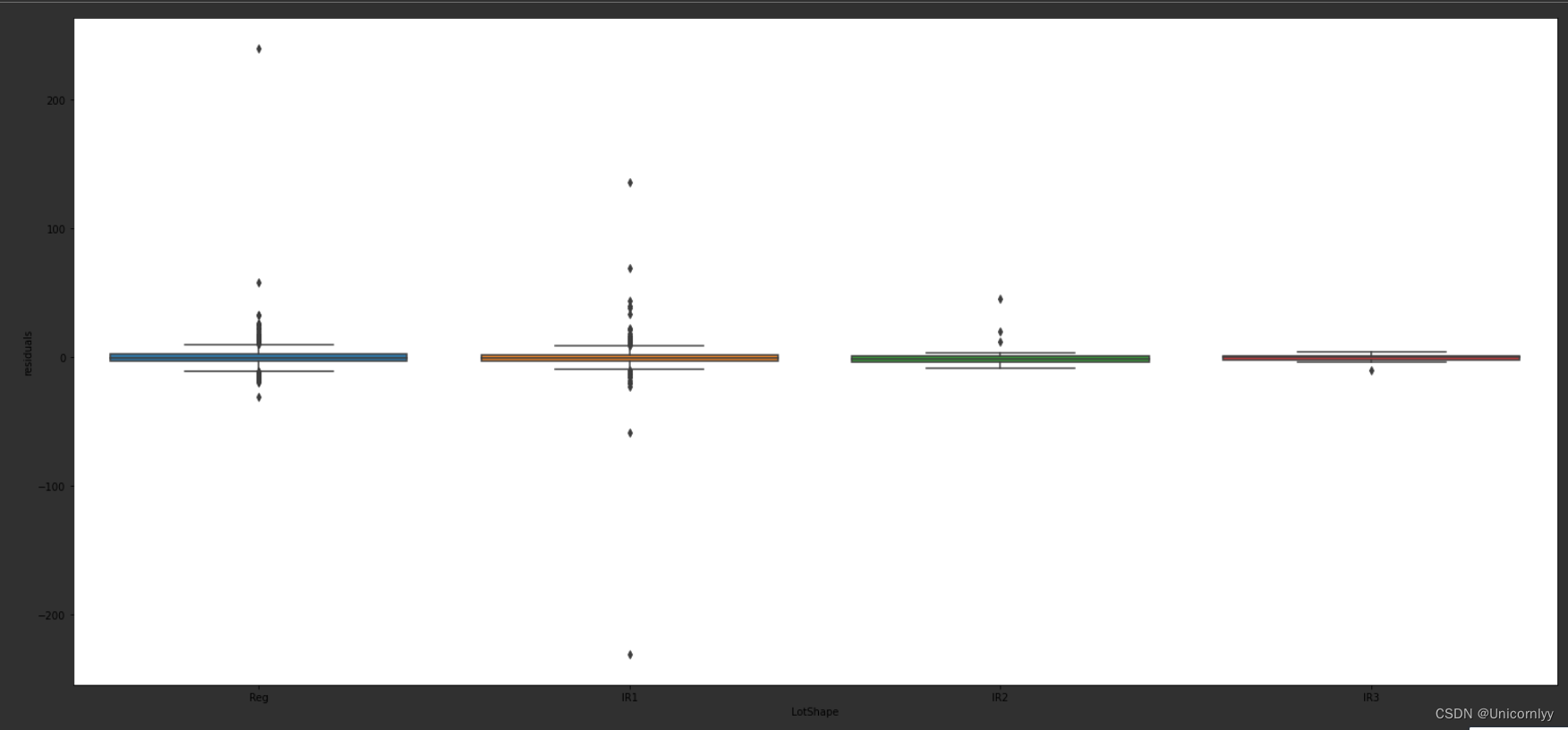
利用 Seaborn 库创建一个箱线图，用于展示 ‘LotShape’ 特征对应的 ‘residuals’ 分布情况，帮助分析不同 ‘LotShape’ 类别下残差的差异和分布情况。

import seaborn as snsvar = 'LotShape'#表示我们希望对数据集中名为 'LotShape' 的特征进行可视化分析
data = pd.concat([train['residuals'], train[var]], axis=1)#训练数据集 train 中的 'residuals'（残差）和 'LotShape' 两列按列拼接起来，形成一个新的 DataFrame data，以便后续进行箱线图的绘制
f, ax = plt.subplots(figsize=(26, 12))
fig = sns.boxplot(x=var, y="residuals", data=data)
#fig.axis(ymin=0, ymax=15);

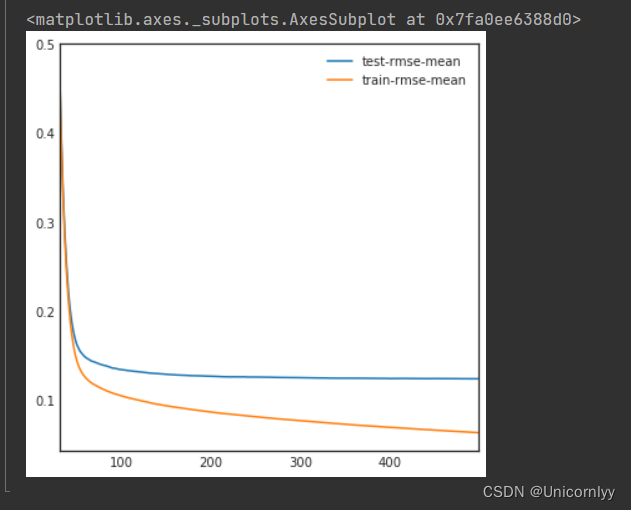
利用 XGBoost 库进行梯度提升树模型的训练和交叉验证，并通过绘制训练过程中的性能指标曲线，帮助分析模型的训练效果和泛化能力

import xgboost as xgb
dtrain = xgb.DMatrix(X_train, label = y)#利用 XGBoost 提供的 DMatrix 函数，将训练数据集 X_train 和对应的标签 y 转换为 XGBoost 内部的数据格式，以便进行后续的模型训练
dtest = xgb.DMatrix(X_test)#同样地，将测试数据集 X_test 转换为 XGBoost 内部的数据格式，以便后续模型的预测使用params = {"max_depth":2, "eta":0.1, 'silent': True}#设置了 XGBoost 模型训练的参数
model = xgb.cv(params, dtrain,  num_boost_round=500, early_stopping_rounds=100)#利用 XGBoost 提供的 cv 函数进行交叉验证训练
model.loc[30:,["test-rmse-mean", "train-rmse-mean"]].plot()#择从第30轮迭代开始到最后的训练误差和测试误差，然后利用 Pandas 的 plot 函数进行可视化展示

数据探索

用来生成关于数据集特征的统计信息的

stats = []
for col in train.columns:stats.append((col, train[col].nunique(), train[col].isnull().sum() * 100 / train.shape[0], train[col].value_counts(normalize=True, dropna=False).values[0] * 100, train[col].dtype))#对每列特征进行统计，并将统计结果以元组的形式添加到 stats 列表中
stats_df = pd.DataFrame(stats, columns=['Feature', 'Unique_values', 'Percentage of missing values', 'Percentage of values in the biggest category', 'type'])#将统计信息转换成 DataFrame 格式，方便查看和分析
stats_df.sort_values('Percentage of missing values', ascending=False)[:10]#按照缺失值百分比降序排列，并显示前10行结果，以便查看缺失值较多的特征

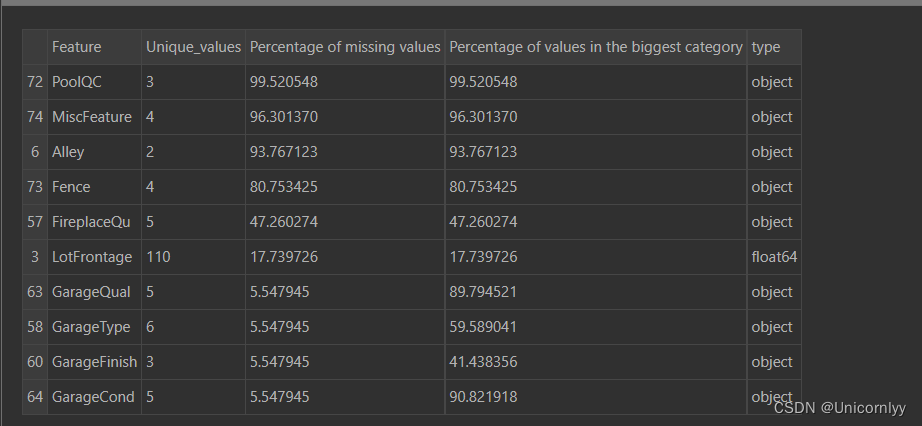
对训练数据集中的缺失值进行统计，并通过条形图可视化展示各个特征的缺失值数量

missing = train.isnull().sum()#统计每个特征的缺失值数量
missing = missing[missing > 0]#留缺失值数量大于 0 的部分
missing.sort_values(inplace=True)#对筛选后的结果进行排序
missing.plot.bar()#将经过排序后的缺失值数量以条形图的形式进行可视化展示

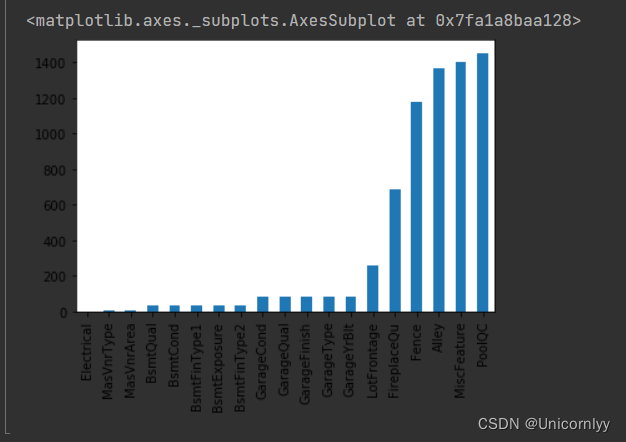
对训练数据集中的缺失值进行统计，并利用条形图清晰展示各个特征的缺失值数量，有助于分析数据集的完整性和预处理中需要处理的缺失值情况。
返回了关于训练数据集中名为 ‘SalePrice’ 的特征（即目标变量）的描述性统计信息

train['SalePrice'].describe()

count 1460.000000
mean 180921.195890
std 79442.502883
min 34900.000000
25% 129975.000000
50% 163000.000000
75% 214000.000000
max 755000.000000
Name: SalePrice, dtype: float64

我们可以得到以下关于 'SalePrice' 特征的具体情况：样本数量（count）为 1460，这意味着数据集中 'SalePrice' 特征的非缺失值数量为 1460。
'SalePrice' 特征的均值（mean）为 180,921.20美元，这表示数据集中 'SalePrice' 的平均售价约为 180,921.20美元。
'SalePrice' 特征的标准差（std）为 79,442.50美元，这说明 'SalePrice' 数据的分布相对分散，即数据的离散程度较大。
'SalePrice' 特征的最小值（min）为 34,900.00美元，意味着数据集中记录的最低售价为 34,900.00美元。
'SalePrice' 特征的第 25% 百分位数（25%）为 129,975.00美元，即 25% 的房屋售价低于或等于 129,975.00美元。
'SalePrice' 特征的中位数（50%）为 163,000.00美元，这表示数据集中 'SalePrice' 的中间值约为 163,000.00美元。
'SalePrice' 特征的第 75% 百分位数（75%）为 214,000.00美元，即 75% 的房屋售价低于或等于 214,000.00美元。
'SalePrice' 特征的最大值（max）为 755,000.00美元，这说明数据集中记录的最高售价为 755,000.00美元。
这些描述性统计信息为我们提供了 'SalePrice' 特征的分布、中心趋势和离散程度等重要信息，有助于我们更好地理解该特征的特点。

绘制经过对数变换后的 ‘SalePrice’ 数据的分布图

import scipy.stats as st
plt.figure(figsize=(9, 8))
sns.distplot(np.log(train['SalePrice']), color='b', bins=100, hist_kws={'alpha': 0.4})

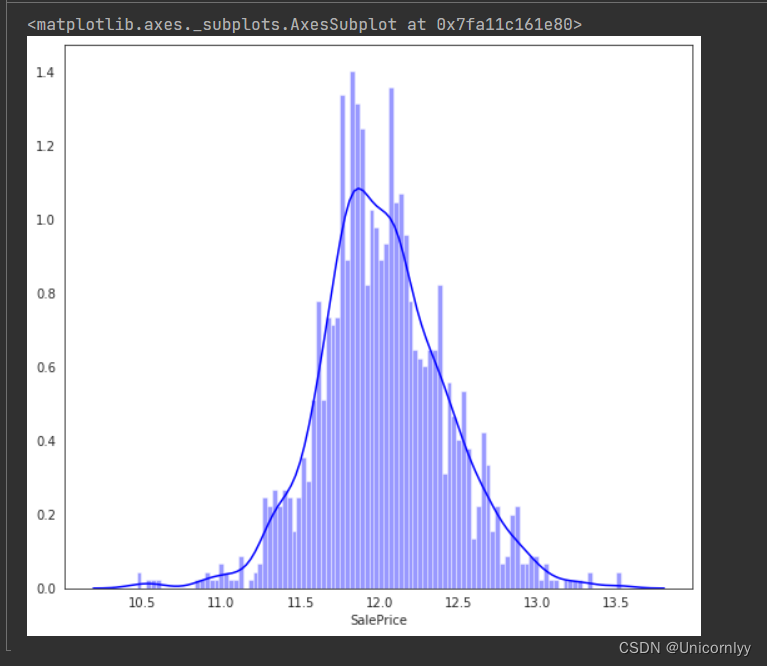
• np.log(train[‘SalePrice’]) 对 ‘SalePrice’ 数据进行了自然对数变换，将其转换为对数值。
• color=‘b’ 设置了图形的颜色为蓝色。
• bins=100 指定了直方图的柱子数量为 100，这样可以更加精细地呈现数据的分布情况。
• hist_kws={‘alpha’: 0.4} 设置了直方图的透明度为 0.4，使得底层的数据分布也能够在一定程度上显示出来。

将数据进行对数变换有几个常见的原因和好处

减小数据的尾部重尾性（long tail）：对于右偏（正偏）分布的数据，即尾部较长的分布，取对数可以压缩数据的动态范围，使得极端值对整体分布的影响减弱。这有助于减小异常值的影响，使得数据更加符合模型的假设。

使数据更加对称：许多统计方法要求数据近似正态分布。对数变换可以把指数增长（或指数衰减）的数据转换成线性增长（或线性衰减），从而更接近正态分布。

稳定方差：在一些情况下，对数变换可以帮助稳定数据的方差，使之更符合线性模型的方差齐性假设。

降低异方差性：对数变换可以缩小随着自变量增大而引起的方差变化，从而减小自变量与因变量之间的离散程度不等的问题。
总的来说，对数变换通常用于改善数据的性质，使之更适合应用于各种统计分析和建模技术。然而，需要注意的是，对数变换并不适用于所有类型的数据，特别是对于含有零值或负值的数据，需要谨慎处理。
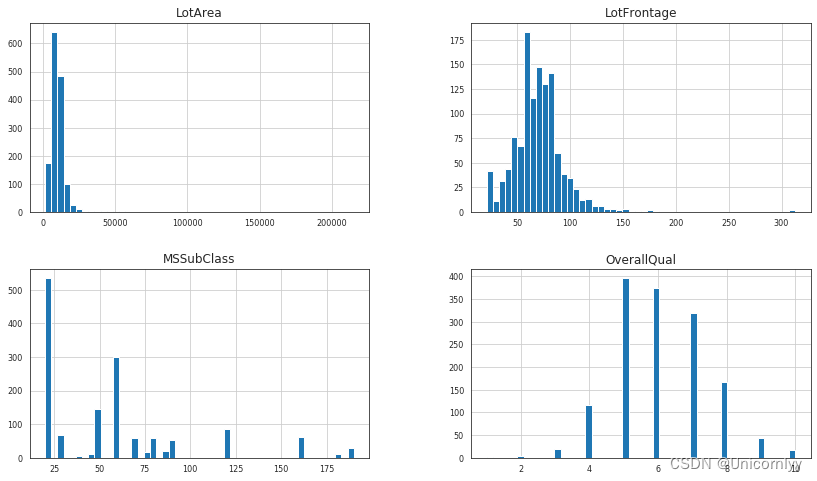
绘制数据集中所有数值型（‘float64’ 和 ‘int64’ 类型）特征的直方图

df_num = train.select_dtypes(include = ['float64', 'int64'])
df_num.hist(figsize=(16, 20), bins=50, xlabelsize=8, ylabelsize=8)

xlabelsize=8, ylabelsize=8 分别设置了 x 轴和 y 轴标签的字体大小为 8，以确保标签清晰可读


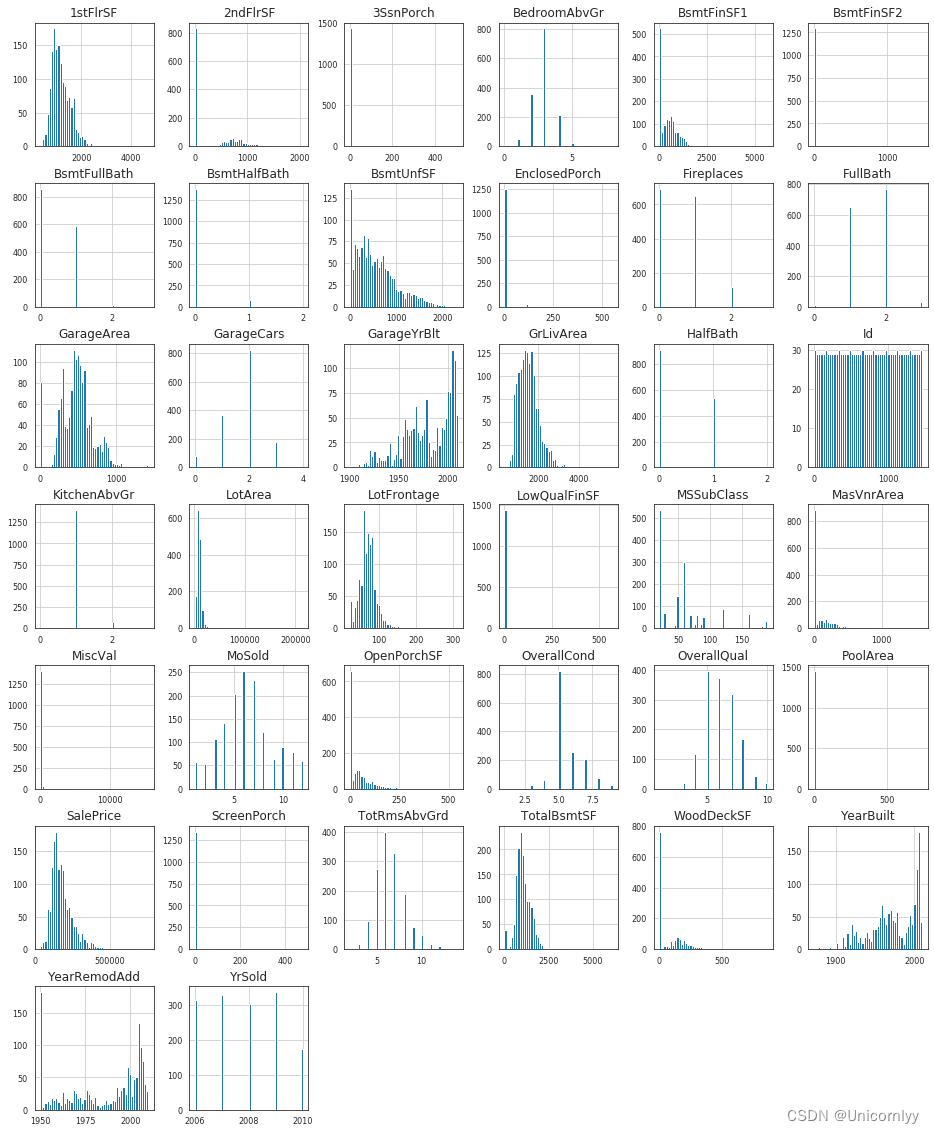
计算数据集中各个数值型特征之间的相关性，并将相关性矩阵以热力图的形式进行可视化

corrmat = train.corr()
f, ax = plt.subplots(figsize=(20, 9))
sns.heatmap(corrmat, vmax=0.8, square=True)

corr() 方法用于计算特征之间的皮尔逊相关系数（Pearson correlation coefficient），反映了两个变量之间的线性相关性程度
相关系数的取值范围在 -1 到 1 之间，0 表示无相关性，-1 表示负相关性，1 表示正相关性
vmax=0.8指定了颜色映射的最大值为 0.8，即相关性系数大于 0.8 的部分会用相应颜色表示。

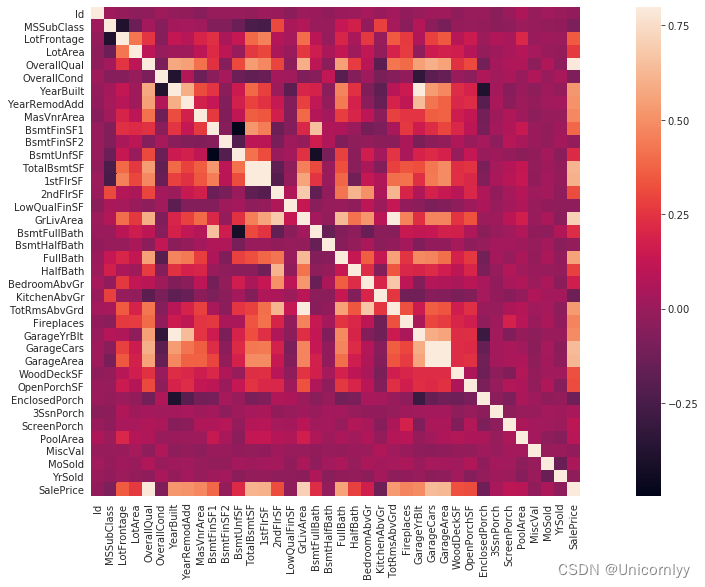
直观地了解数据集中各个数值型特征之间的相关性强弱，从而帮助你识别出潜在的多重共线性问题、选择特征、以及了解特征之间的关联性。这有助于进一步进行特征选择、降维处理和建模分析。
主要用于对数据集中的分类型（非数值型）特征进行可视化分析

df_not_num = train.select_dtypes(include = ['O'])#筛选出所有的非数值型特征字符串类型
fig, axes = plt.subplots(round(len(df_not_num.columns) / 3), 3, figsize=(12, 30))#计算了需要创建的子图行数，其中每行最多包含三个子图for i, ax in enumerate(fig.axes):if i < len(df_not_num.columns):#设置 x 轴标签的旋转角度，确保标签不会重叠ax.set_xticklabels(ax.xaxis.get_majorticklabels(), rotation=45)sns.countplot(x=df_not_num.columns[i], alpha=0.7, data=df_not_num, ax=ax)fig.tight_layout()#调整子图的布局，确保它们之间的间距合适，不会重叠

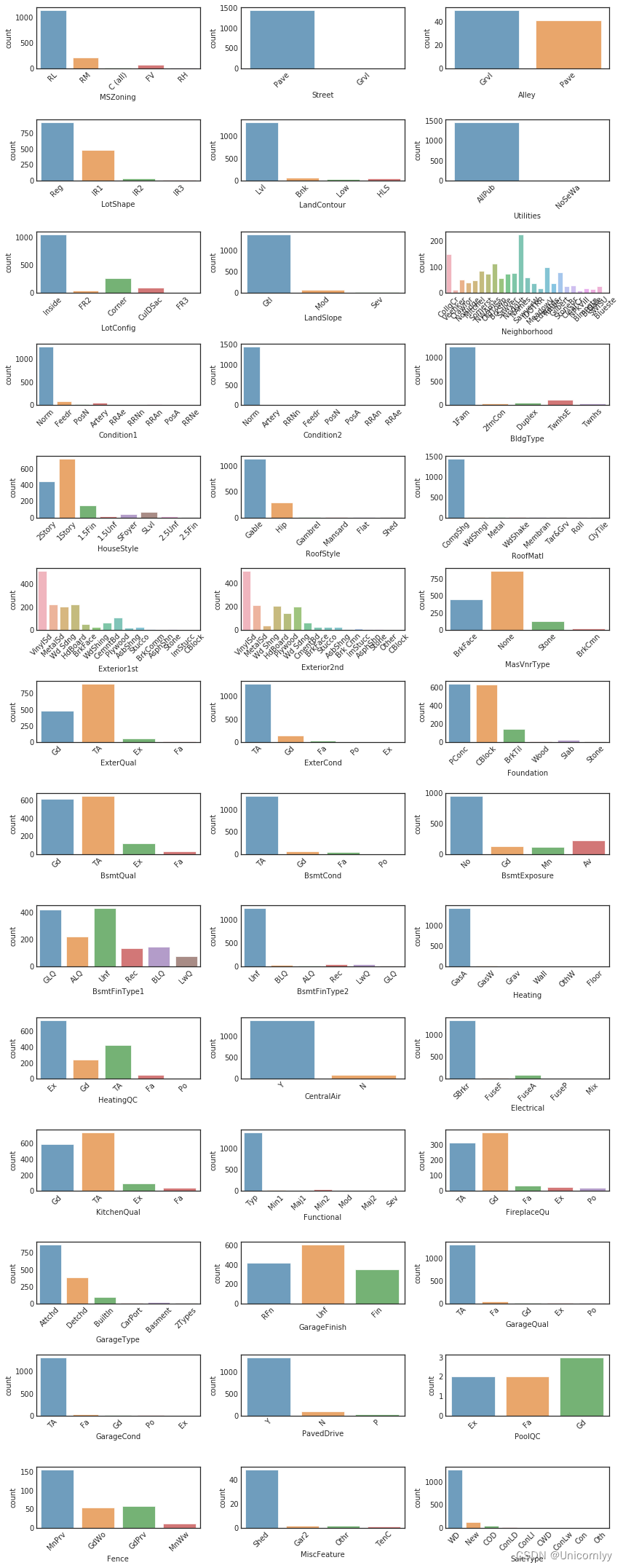
在一个图形窗口中同时观察多个分类型特征的计数分布，有助于你快速了解这些特征的取值分布情况，发现异常值或者不平衡的类别分布。这有助于后续进行特征工程和建模分析。
对数据集中的数值型特征进行直方图可视化分析

df_num = train.select_dtypes(include = ['float64', 'int64'])
df_num = df_num[df_num.columns.tolist()[1:5]]
df_num.hist(figsize=(14, 8), bins=50, xlabelsize=8, ylabelsize=8)

创建一个堆叠条形图，展示了按照不同的“Neighborhood”和“OverallQual”分组的数据计数情况

plt.style.use('seaborn-white')#设置了绘图样式为 seaborn-white，这是 seaborn 库提供的一种风格，能够美化图表的外观
type_cluster = train.groupby(['Neighborhood','OverallQual']).size()#对数据集 train 按照“Neighborhood”和“OverallQual”两个特征进行分组，并统计每个分组的样本数量
type_cluster.unstack().plot(kind='bar',stacked=True, colormap= 'PuBu', figsize=(13,11),  grid=False)#
plt.xlabel('OverallQual', fontsize=16)
plt.show()

unstack() 方法将多层索引的数据重新排列，使得每个“Neighborhood”对应一列数据。
kind=‘bar’ 指定了绘图类型为条形图。
stacked=True 设置了堆叠参数为 True，使得不同的“Neighborhood”在同一个“OverallQual”下的条形块可以堆叠显示。
colormap= ‘PuBu’ 指定了条形图的颜色映射为 PuBu，即蓝紫色系。
figsize=(13,11) 设置了图形窗口的大小为 13x11 英寸。
grid=False 关闭了图表的网格线显示

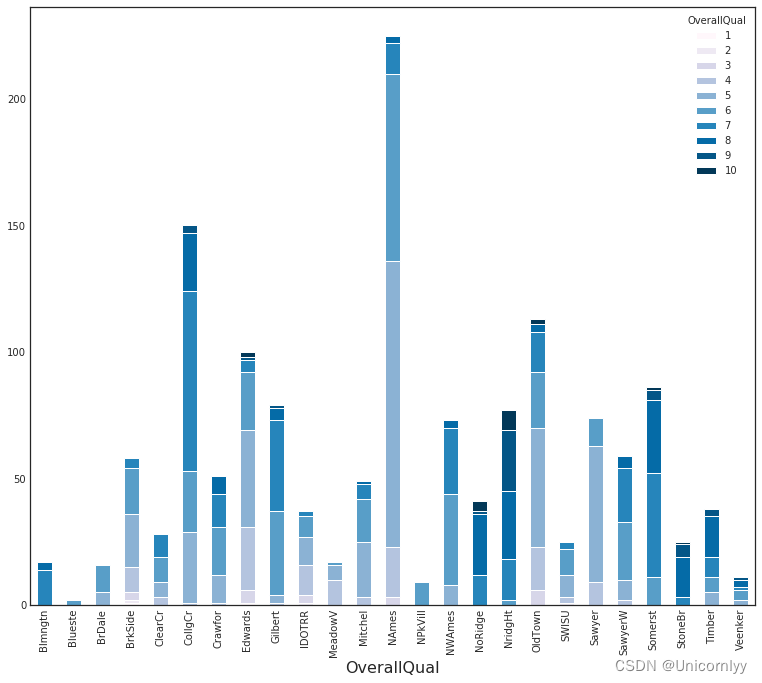
通过这段代码，你可以清楚地观察到不同“Neighborhood”在不同“OverallQual”下的样本数量分布情况，从而更好地理解这两个特征之间的关联。这有助于发现特征之间的内在模式和规律，为进一步的数据分析和建模提供参考
创建一个箱线图，用以展示不同街区（Neighborhood）的房屋销售价格（SalePrice）分布情况

var = 'Neighborhood'
data = pd.concat([train['SalePrice'], train[var]], axis=1)#将 'SalePrice' 和 'Neighborhood' 两列沿列方向拼接，组成一个新的 DataFrame，并将其赋值给变量 data
f, ax = plt.subplots(figsize=(26, 12))
fig = sns.boxplot(x=var, y="SalePrice", data=data)#这行代码定义了变量 var，将其设为字符串 'Neighborhood'，表示我们希望探索房屋销售价格与街区之间的关
fig.axis(ymin=0, ymax=15);

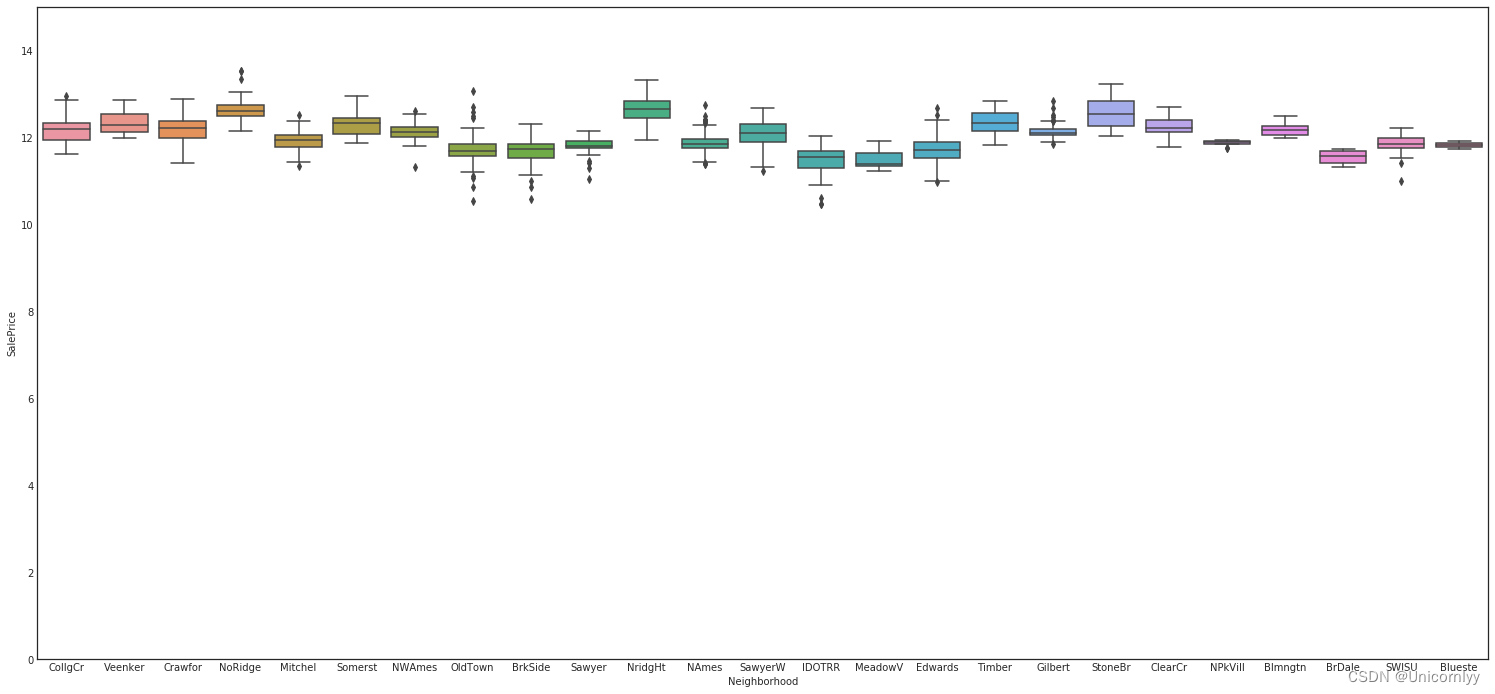
直观地观察到不同街区房屋销售价格的分布情况，包括中位数、四分位数、异常值等统计信息。这有助于比较不同街区的房屋价格水平和分布差异，为进一步分析不同街区的房地产市场提供参考
箱线图：
最小值，第一个四分位点（25%），中位数，第三个四分位点（75%），最大值，离群值

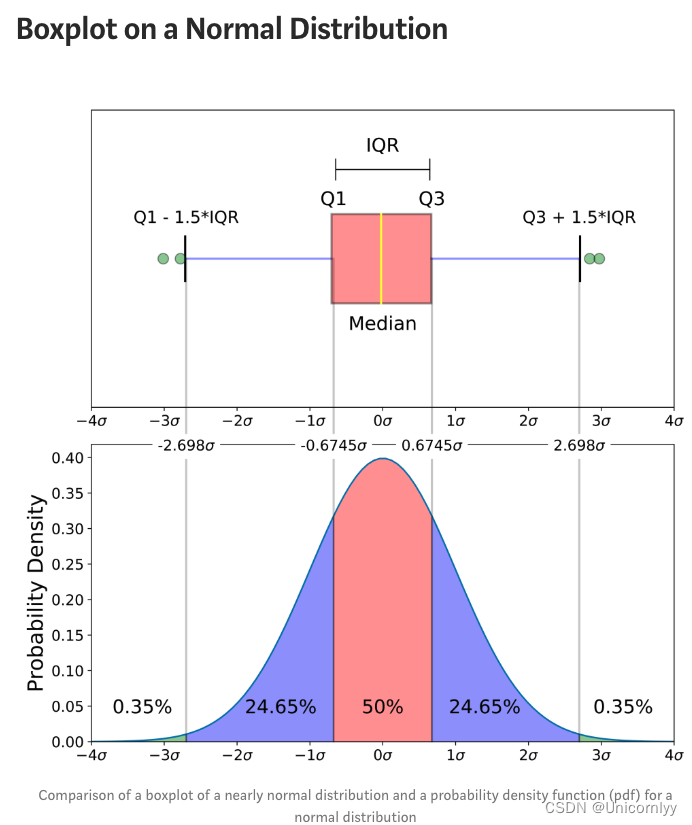
参考链接

特征工程

主要用于数据预处理，包括合并训练集和测试集、删除缺失值比例大于50%的特征列以及对object类型的缺失特征进行填充

test = pd.read_csv("test.csv")
train = pd.read_csv("train.csv")
ntrain = train.shape[0]
ntest = test.shape[0]data = pd.concat([train, test], axis=0, sort=False)
# 删除缺失值比例大于50%的特征列
missing_cols = [c for c in data if data[c].isna().mean()*100 > 50]
data = data.drop(missing_cols, axis=1)# 对object型的缺失特征进行填充
object_df = data.select_dtypes(include=['object'])
numerical_df = data.select_dtypes(exclude=['object'])#将数值类型（numerical）特征列存储在变量 numerical_df 中。select_dtypes 函数根据指定的数据类型选择DataFrame中的列object_df = object_df.fillna('unknow')

对数值类型的缺失特征进行填充，

missing_cols = [c for c in numerical_df if numerical_df[c].isna().sum() > 0]#numerical_df[c].isna().sum() 的含义是计算特征列 c 中缺失值的数量，> 0 表示有缺失值
for c in missing_cols:numerical_df[c] = numerical_df[c].fillna(numerical_df[c].median())#计算特征列 c 的中位数，并将缺失值替换为该中位数值

针对对象类型的DataFrame object_df，删除了其中的特定列

object_df = object_df.drop(['Heating','RoofMatl','Condition2','Street','Utilities'],axis=1)

numerical_df.loc[numerical_df['YrSold'] < numerical_df['YearBuilt'], 'YrSold' ] = 2009#通过条件 numerical_df['YrSold'] < numerical_df['YearBuilt'] 找到了在售年份早于建造年份的数据记录，然后将这些数据中的'YrSold'列值赋值为 2009。这可能是因为房屋出售年份早于建造年份显然是不合理的情况，所以进行了修正
numerical_df['Age_House']= (numerical_df['YrSold'] - numerical_df['YearBuilt'])#计算了房屋的年龄，它通过减法操作计算了'YrSold'列和'YearBuilt'列的差值，将结果存储在名为 'Age_House' 的新列中，表示房屋的年龄

通过上述代码，数据集中的房屋出售年份早于建造年份的数据得到了修正，并且新的房屋年龄特征被创建，有助于后续的分析和建模~
用于创建新的特征列，分别表示地下室浴室总数、总浴室数和总面积

numerical_df['TotalBsmtBath'] = numerical_df['BsmtFullBath'] +numerical_df['BsmtHalfBath']*0.5#通过将地下室全浴室数量与地下室半浴室数量乘以0.5相加，得到了地下室浴室的总数，并将结果存储在名为 'TotalBsmtBath' 的新列中
numerical_df['TotalBath'] = numerical_df['FullBath'] + numerical_df['HalfBath']*0.5 #通过将完整浴室数量与半浴室数量乘以0.5相加，得到了总浴室的数量，并将结果存储在名为 'TotalBath' 的新列中
numerical_df['TotalSA'] = numerical_df['TotalBsmtSF'] + numerical_df['1stFlrSF'] +\
numerical_df['2ndFlrSF']#计算了总面积。它通过将地下室总面积、一楼总面积和二楼总面积相加，得到了房屋的总面积，并将结果存储在名为 'TotalSA' 的新列中

新的特征列被创建，用于表示地下室浴室总数、总浴室数和总面积。这些新的特征有助于提供更多关于房屋属性的信息，可能对后续的分析和建模有帮助
主要用于将一些分类特征映射为数值特征，将每个分类值对应一个数值，以便后续的数据分析和建模过程中使用~

bin_map  = {'TA':2,'Gd':3, 'Fa':1,'Ex':4,'Po':1,'None':0,
'Y':1,'N':0,'Reg':3,'IR1':2,'IR2':1, \
'IR3':0,"None" : 0,"No" : 2, "Mn" : 2, 
"Av": 3,"Gd" : 4,"Unf" : 1, "LwQ": 2, \
"Rec" : 3,"BLQ" : 4, "ALQ" : 5, "GLQ" : 6}
object_df['ExterQual'] = object_df['ExterQual'].map(bin_map)#将 'ExterQual' 列中的分类值映射为相应的数值。例如，如果 'ExterQual' 列的值为 'TA'，则它将被映射为 2
object_df['ExterCond'] = object_df['ExterCond'].map(bin_map)
object_df['BsmtCond'] = object_df['BsmtCond'].map(bin_map)
object_df['BsmtQual'] = object_df['BsmtQual'].map(bin_map)
object_df['HeatingQC'] = object_df['HeatingQC'].map(bin_map)
object_df['KitchenQual'] = object_df['KitchenQual'].map(bin_map)
object_df['FireplaceQu'] = object_df['FireplaceQu'].map(bin_map)
object_df['GarageQual'] = object_df['GarageQual'].map(bin_map)
object_df['GarageCond'] = object_df['GarageCond'].map(bin_map)
object_df['CentralAir'] = object_df['CentralAir'].map(bin_map)
object_df['LotShape'] = object_df['LotShape'].map(bin_map)
object_df['BsmtExposure'] = object_df['BsmtExposure'].map(bin_map)
object_df['BsmtFinType1'] = object_df['BsmtFinType1'].map(bin_map)
object_df['BsmtFinType2'] = object_df['BsmtFinType2'].map(bin_map)PavedDrive = {"N" : 0, "P" : 1, "Y" : 2}#定义了一个字典，用于将 'PavedDrive' 列中的分类值映射为相应的数值。例如，如果 'PavedDrive' 列的值为 'N'，则它将被映射为 0。

将一些列中的分类值映射为数值特征，这些数值特征可以更方便地在后续的数据分析和建模过程中使用。同时，这样的映射也可以将原始的分类特征转换为连续的数值特征，有助于提高模型的准确性和效果。
进行剩余的 object 特征的处理，包括对 PavedDrive 列的映射、选择剩余的 object 特征以及进行 one-hot 编码，并将处理后的特征与 numerical_df 数据拼接在一起，并赋值给 data 变量

object_df['PavedDrive'] = object_df['PavedDrive'].map(PavedDrive)
# 选择剩余的object特征
rest_object_columns = object_df.select_dtypes(include = ['object'])
# 进行one-hot编码
object_df = pd.get_dummies(object_df, columns = rest_object_columns.columns) #使用 get_dummies 函数对 object_df 中的 object 特征进行 one-hot 编码。该函数将每个 object 特征拆分为多个二进制特征列，每个特征列对应一个分类值，如果原始特征的某个值出现在数据中，则对应的特征列取值为 1，否则取值为 0。这样可以将 object 特征转换为数值特征，以便后续的数据分析和建模过程中使用data = pd.concat([object_df, numerical_df], axis=1, sort=False)#将处理后的 object_df 数据与 numerical_df 数据在列方向上进行拼接，并赋值给 data 变量。这样就得到了包含所有特征的最终数据集，用于后续的数据分析和建模

对剩余的 object 特征进行了处理，包括映射、one-hot 编码，最终得到了包含所有特征的 data 数据集。这样的处理可以使数据更适合用于机器学习模型的训练和预测。

离散特征的编码分为两种情况：
1、离散特征的取值之间没有大小的意义，比如color：[red,blue],那么就使用one-hot编码

2、离散特征的取值有大小的意义，比如size:[X,XL,XXL],那么就使用数值的映射{X:1,XL:2,XXL:3}

独热编码优缺点：
优点：独热编码解决了分类器不好处理属性数据的问题，在一定程度上也起到了扩充特征的作用。它的值只有0和1，不同的类型存储在垂直的空间。
缺点：当类别的数量很多时，特征空间会变得非常大。在这种情况下，一般可以用PCA来减少维度。而且one hot encoding+PCA这种组合在实际中也非常有用
什么时候用独热编码？
用：独热编码用来解决类别型数据的离散值问题
不用：将离散型特征进行one-hot编码的作用，是为了让距离计算更合理，但如果特征是离散的，并且不用one-hot编码就可以很合理的计算出距离，那么就没必要进行one-hot编码。有些基于树的算法在处理变量时，并不是基于向量空间度量，数值只是个类别符号，即没有偏序关系，所以不用进行独热编码。 Tree Model不太需要one-hot编码： 对于决策树来说，one-hot的本质是增加树的深度
独热编码参考

特征选择

用来找出数据集中具有高相关性的特征，并将这些高相关性的特征名存储在 col_corr 集合中

def correlation(data, threshold):col_corr = set() corr_matrix = data.corr() # 计算数据集中各特征之间的相关系数矩阵for i in range(len(corr_matrix.columns)):for j in range(i):if abs(corr_matrix.iloc[i, j]) > threshold:  # 相似性分数与阈值对比colname = corr_matrix.columns[i]  # 获取列名col_corr.add(colname)
return col_corr

通过计算相关系数矩阵，找出了具有高相关性的特征，并将它们的特征名存储在集合 col_corr 中。这样的函数可以帮助我们识别出数据集中存在较强相关性的特征，从而有针对性地进行特征选择或降维处理

用于找出数据集中与目标变量（‘SalePrice’）具有高相关性的特征，并将这些特征存储在 corr_features 中

all_cols = [c for c in data.columns if c not in ['SalePrice']]#筛选出不包括 'SalePrice' 的所有列，将其存储在 all_cols 变量中
corr_features = correlation(data[all_cols], 0.9)#调用了之前定义的 correlation 函数，计算了除了 'SalePrice' 外的所有特征列与彼此之间的相关性，并将相关性大于 0.9 的特征名存储在 corr_features 中

这段代码的作用是找出数据集中与 ‘SalePrice’ 不相关的特征，并将这些特征名存储在 corr_features 中。这样的操作可以帮助我们识别出不适合作为预测目标的特征，或者进行进一步的特征选择和模型建立的准备工作

模型融合

导入库函数

import numpy as np
import pandas as pd
from sklearn.model_selection import KFold
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import OneHotEncoder
import lightgbm as lgbfrom matplotlib import colors 
from matplotlib.ticker import PercentFormatter 
import matplotlib.pyplot as plt
import time
import warnings
warnings.filterwarnings('ignore')

执行了一系列数据预处理步骤，准备将数据分成训练集和测试集。

train = pd.read_csv('train.csv')
test = pd.read_csv('test.csv')all_data = pd.concat((train,test))
all_data = pd.get_dummies(all_data)#使用 pd.get_dummies 函数对 all_data 进行独热编码（One-Hot Encoding），将分类变量转换为哑变量，并将其存储回 all_data 中。这一步可以帮助将分类特征转换为模型可以直接处理的数值特征
# 填充缺失值
all_data = all_data.fillna(all_data.mean())#填充缺失值：将 all_data 中的缺失值用各列的均值进行填充。这有助于保持数据完整性，以便后续的建模过程不会因为缺失值而产生错误
# 数据切分
x_train = all_data[:train.shape[0]]
x_test = all_data[train.shape[0]:]
y_train = train.SalePrice#将处理好的数据集 all_data 划分回训练集 x_train 和测试集 x_test。同时，从训练集中提取出目标变量 SalePrice，存储在 y_train 中

作用是进行了数据的读取、合并、独热编码、缺失值填充和数据切分等预处理步骤，为后续的建模工作做好了准备
实现了一个集成学习的框架，使用了几个回归模型（ExtraTreesRegressor、RandomForestRegressor、Ridge、Lasso）以及评估指标（均方根误差）进行房价预测任务

#导入了所需的库和模块
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import Ridge, Lasso
from math import sqrt  
# 依然采用5折交叉验证 
kf = KFold(n_splits=5, shuffle=True, random_state=2020)                                                                                                                                                                                                                                   
#定义了一个SklearnWrapper类，作为对Scikit-learn模型的封装，方便后续的训练和预测操作
class SklearnWrapper(object):def __init__(self, clf, seed=0, params=None):params['random_state'] = seedself.clf = clf(**params)def train(self, x_train, y_train):self.clf.fit(x_train, y_train)def predict(self, x):return self.clf.predict(x)
#构造函数初始化了一个回归模型，并使用给定的参数进行模型初始化。train方法用于训练模型，predict方法用于进行预测
#接下来定义了一个函数get_oof，用于进行交叉验证和集成学习
def get_oof(clf):oof_train = np.zeros((x_train.shape[0],))oof_test = np.zeros((x_test.shape[0],))oof_test_skf = np.empty((5, x_test.shape[0]))for i, (train_index, valid_index) in enumerate(kf.split(x_train, y_train)):trn_x, trn_y, val_x, val_y = x_train.iloc[train_index], y_train[train_index],\x_train.iloc[valid_index], y_train[valid_index]clf.train(trn_x, trn_y)oof_train[valid_index] = clf.predict(val_x)oof_test_skf[i, :] = clf.predict(x_test)oof_test[:] = oof_test_skf.mean(axis=0)return oof_train.reshape(-1, 1), oof_test.reshape(-1, 1)

实现了一个集成学习框架，通过交叉验证和模型集成来对房价进行预测。通过定义SklearnWrapper类封装Scikit-learn模型，方便进行训练和预测操作。使用KFold对象进行交叉验证，获取了训练集和测试集的预测结果。
定义了一些参数和模型后，使用SklearnWrapper类对四种不同的回归模型（ExtraTreesRegressor、RandomForestRegressor、Ridge、Lasso）进行了实例化，并调用get_oof函数进行交叉验证和集成学习

et_params = {'n_estimators': 100,'max_features': 0.5,'max_depth': 12,'min_samples_leaf': 2,
}
rf_params = {'n_estimators': 100,'max_features': 0.2,'max_depth': 12,'min_samples_leaf': 2,
}
rd_params={'alpha': 10}
ls_params={ 'alpha': 0.005}
et = SklearnWrapper(clf=ExtraTreesRegressor, seed=2020, params=et_params)
rf = SklearnWrapper(clf=RandomForestRegressor, seed=2020, params=rf_params)
rd = SklearnWrapper(clf=Ridge, seed=2020, params=rd_params)
ls = SklearnWrapper(clf=Lasso, seed=2020, params=ls_params)et_oof_train, et_oof_test = get_oof(et)
rf_oof_train, rf_oof_test = get_oof(rf)
rd_oof_train, rd_oof_test = get_oof(rd)
ls_oof_train, ls_oof_test = get_oof(ls)

(1460,)
(1460,)
(1460,)
(1460,)
这段代码实现了对多个回归模型进行参数初始化、交叉验证和集成学习的过程，为房价预测任务提供了多种模型的预测结果。
实现了一个堆叠模型（stacking model），用于将多个基本模型的预测结果进行堆叠，并使用线性回归模型进行最终的集成预测

def stack_model(oof_1, oof_2, oof_3, oof_4, predictions_1, predictions_2, predictions_3, predictions_4, y):
## 将各个基本模型的训练集和测试集预测结果进行水平堆叠train_stack = np.hstack([oof_1, oof_2, oof_3, oof_4])test_stack = np.hstack([predictions_1, predictions_2, predictions_3, predictions_4])# 初始化存储最终结果的数组oof = np.zeros((train_stack.shape[0],))predictions = np.zeros((test_stack.shape[0],))scores = []for fold_, (trn_idx, val_idx) in enumerate(kf.split(train_stack, y)): # 从堆叠后的训练集数据中分割出训练集和验证集trn_data, trn_y = train_stack[trn_idx], y[trn_idx]val_data, val_y = train_stack[val_idx], y[val_idx]# 使用Ridge回归模型进行训练clf = Ridge(random_state=2020)clf.fit(trn_data, trn_y)# 对验证集和测试集进行预测oof[val_idx] = clf.predict(val_data)predictions += clf.predict(test_stack) / 5# 计算并存储每折的均方根误差score_single = sqrt(mean_squared_error(val_y, oof[val_idx]))scores.append(score_single)print(f'{fold_+1}/{5}', score_single)# 输出每折的均方根误差print('mean: ',np.mean(scores))return oof, predictionsoof_stack , predictions_stack  = stack_model(et_oof_train, rf_oof_train, rd_oof_train, ls_oof_train, \et_oof_test, rf_oof_test, rd_oof_test, ls_oof_test, y_train)

在这部分代码中，stack_model函数首先将四个基本模型的训练集和测试集预测结果进行水平堆叠，然后使用Ridge回归模型对堆叠后的数据进行训练，并进行交叉验证。最终返回堆叠后的训练集预测结果和测试集预测结果。

最后一行代码调用了stack_model函数，并传入了四个基本模型的训练集预测结果（et_oof_train, rf_oof_train, rd_oof_train, ls_oof_train）、测试集预测结果（et_oof_test, rf_oof_test, rd_oof_test, ls_oof_test）以及训练集标签（y_train）进行堆叠模型的训练和预测。

From机器学习算法竞赛实战，王贺、刘鹏、钱乾著