一.向量引入:
向量:只由大小和方向决定,不由位置决定。

二.向量加减法


向量的加法是首尾相连,减法是尾尾相连。
而向量v+向量w为平行四边形主对角线。
向量v-向量w为平行四边形副对角线。
2.向量内积点乘(内积)

内积表示的是cos夹角的大小,如果内积大于0,表示两向量的夹角小于90度,等于0两向量夹角为90度,小于0夹角大于90度。
3.叉乘(外积)

叉乘的几何意义是平行四边形的面积。
三.线性相关理解
有一组向量,a,b,c。有任意系数,x,y,z。a*x+b*y+c*z=0;如果a,b,c三个向量线性无关,那么只有当x=y=z=0时结果才为0。也说明三个向量,两两必有夹角。(不共线)
如果线性相关,那么a,b,c,中,至少有一个与另一个共线,夹角为0。也就是说某一个向量可以拉伸成为另一个向量。
n个线性无关的向量可以通过线性组合张成一个n维空间。
在几何上:
线性相关:组向量中有多余向量,把它去掉后不影响张成空间。
线性无关:没多余向量,去掉任何一个都会影响原有的张成空间,每一个向量都代表了一个新的维度。
例如我们二维平面----->直角坐标系。标准正交基时两两垂直、长度为1的向量可以张成。(1,0)代表x轴方向,(0,1)代表y轴方向。分别用坐标表示[(1,0)T,(0,1)T]。假如我们要直角坐标系中向量(2,3)。只需要改变这个正交基向量组的系数就可以了。2*(1,0)+3(0,1)=(2,0)+(0,3)=(2,3)。
表示向量(2,3)在x轴方向走了2步。y轴方向走了3步。
三.矩阵:
每一个向量构成矩阵的列向量。
上边我们用了正交基向量((1,0),(0,1))获得向量(2,3),相当于拉伸了正交基向量。
而这个用矩阵来描述就是进行了线性变换。[(1,0)T,(0,1)T][2,3]=[2,3],表示由正交基变量组成的矩阵与系数矩阵[2,3]相乘。它的几何意义是向量(2,3)在由正交基坐标系下的映射。如果不是正交基所组成的矩阵,而是别的,[2,3]在别的基构成的坐标系中又会是别的点。而我们如果要把别的基的点转到直角坐标系下,那么就要乘该矩阵的逆矩阵。一个矩阵乘它的逆矩阵等于单位矩阵。例如我们[(0,1)T,(1,1)T][x,y]=[2,3],在基[0,1][1,1]下,在平面直角坐标系中的向量(x,y),线性变换在此坐标系下面是[2,3],如果我们要求(x,y),就要变到直角坐标系下。只需要左乘[(0,1)T,(1,1)T]-1(逆矩阵),那么就是E[x,y]=[(0,1)T,(1,1)T]-1[2,3]。E为单位矩阵,也是直角坐标系。
秩:矩阵(向量组)可以张成空间的维度,用r表示。
奇异矩阵:行列式为0的矩阵,也就是维度变小的矩阵。不满秩的矩阵。但我们不知道维度变得是多小,比如由三维到二维是小,从三围到一维也是小。
非奇异矩阵:行列式不为0的矩阵。满秩矩阵,维度不变的矩阵。
逆矩阵:如果矩阵A,B,AB=BA,那么说明A可逆,写作A^-1。
下面是矩阵的一下运算规则
求逆矩阵:

所以我们知道,矩阵可逆的充要条件是矩阵行列式不为0。


四.行列式
几何意义:二维中,是由基围成的平行四边形面积。
在三维中,是由基围成的平行六面体体积。

如果行列式为0,就相当于没有面积,也就是说被压缩到更小维度,如直角坐标系维度到一条坐标轴。
所以,我们用矩阵的秩来描述就是,满秩矩阵<=>行列式不为0,不满秩矩阵,<=>行列式为0。秩是用来表示线性无关的向量数量,不满秩,就相当于没围起来,就没有面积,行列式为0。
下面是行列式的性质和运算规则。


余子式和代数余子式



五.次线性方程组的解


用矩阵的线性变换求解方程组


初等矩阵:对单位矩阵进行一次初等行变换所得到的矩阵。
初等行变换实际上就是初等矩阵与矩阵间的乘法。
下面涉及高等数学微分方程的内容:


特征值求法

一个矩阵乘一个特征向量的矩阵,等于特征值(标量)乘特征向量的矩阵。
为了更好表示,我们移项,让特征值乘单位矩阵。因为等号右边为0,说明空间被压缩。
特征向量的特点是经过变换后会停留在原来的直线上。相当于被拉伸或者缩减多少倍。
被拉伸或缩减多少倍就是特征值。
粗鄙理解:假设v在直角坐标系E下停留在x轴,用矩阵乘法表示为E*v,那么假设A也代表一个不同于直角坐标系的坐标系,那么在A*v的情况下,如果v还停留在x轴,但是只是被拉伸或是压缩,那么我们就说v是特征向量。
特征向量不为0,那么只能它的左边那部分为0。
于是转化成求解左边为0的情况。

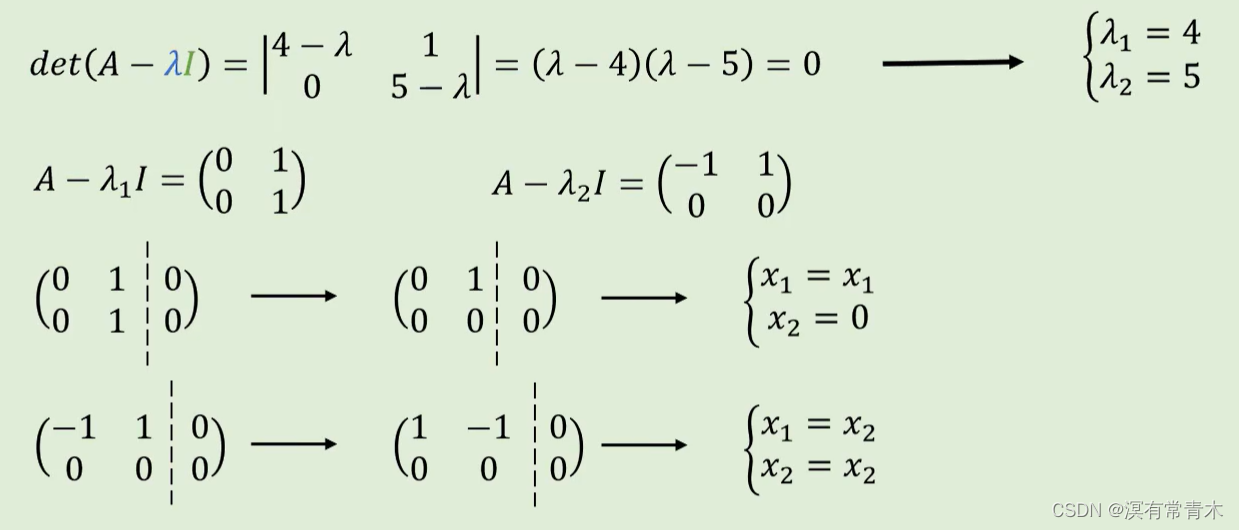
下面A为特征向量矩阵。


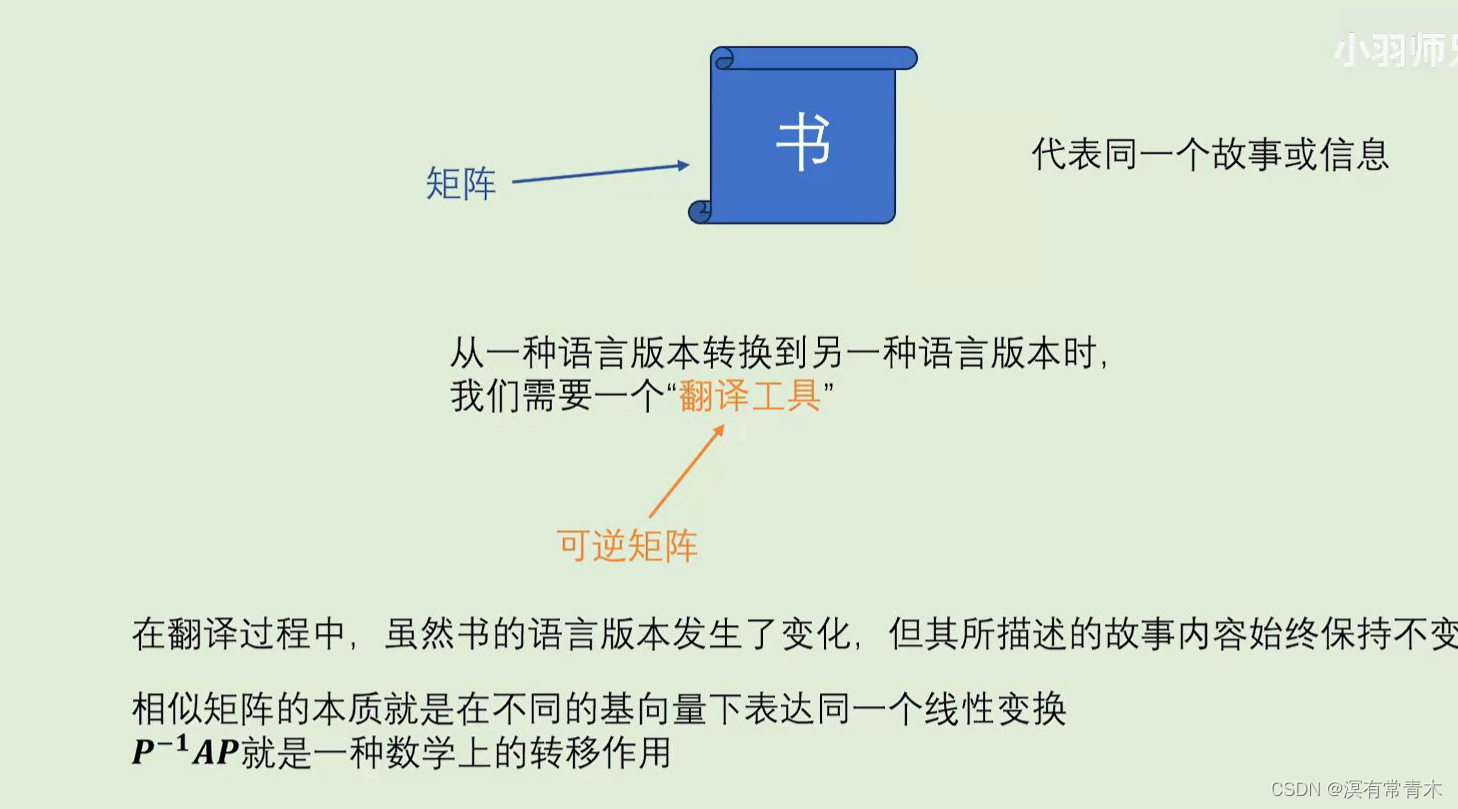



六.二次型





有交叉项是斜的,没交叉项则是正的圆。标准化就是将斜的摆正的过程。


以上截图来自于B站小宇师兄聊考研。作者去学习并有一些自己的理解。