Docker是一种基于容器的虚拟化技术,它允许开发者将应用程序及其依赖项打包到一个轻量级容器中,然后在任何可用的开发、测试和生产环境中进行部署和运行。
下面是Docker的基本概念和优势:
-
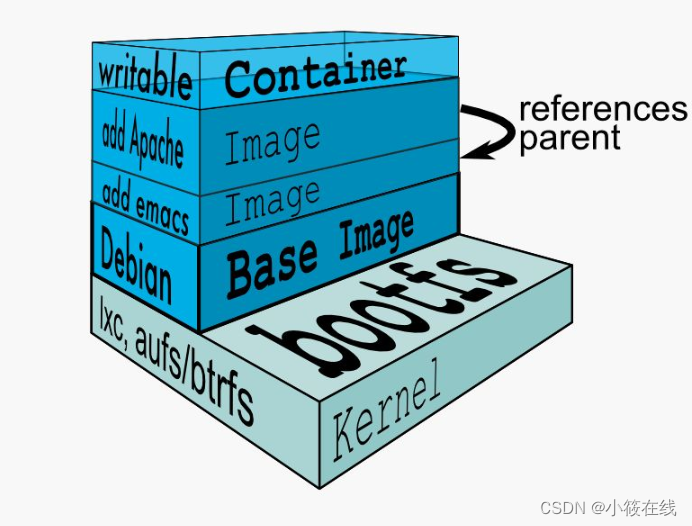
容器:Docker容器是一种独立运行的软件包,包括应用程序、运行时环境、系统工具、库和依赖项。它们可以轻松地从一个环境迁移到另一个环境,而不会受到环境变化的影响。
-
镜像:Docker镜像是一个只读的模板,它包含了创建Docker容器所需的所有指令和文件。开发者可以选择一个现有的Docker镜像,或者根据自己的需要创建一个新的。
-
Dockerfile:Dockerfile是一个文本文件,其中包含了创建Docker镜像的指令和说明。Docker根据Dockerfile构建镜像,这样开发者就可以轻松地创建、复制和共享镜像。
-
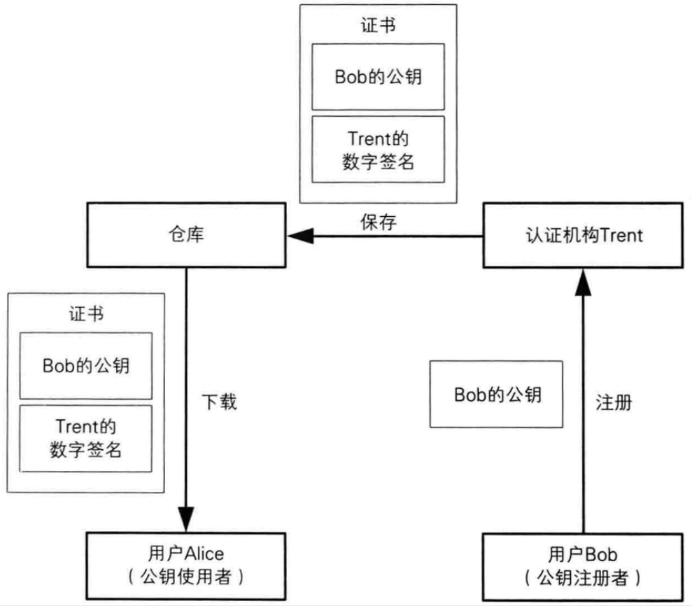
Docker Hub:Docker Hub是Docker官方的云服务,提供了一个中央的存储库,供开发者上传、下载和共享Docker镜像。
Docker的优势:
-
轻量级:Docker容器比虚拟机更轻量级,因为它们不需要启动完整的操作系统。这使得容器更快、更节省资源,并且可以在更复杂的应用程序环境中运行。
-
可移植性:Docker容器可以轻松地从一个环境迁移到另一个环境,而不会受到环境变化的影响。这使得开发者在不同的环境中测试和部署应用程序变得更加容易。
-
一致性:使用Docker容器可以确保应用程序在不同的环境中保持一致性。这使得开发者能够更加自信地部署应用程序,并减少由环境变化引起的错误。
在应用程序开发中,Docker的实际应用有很多。例如,开发者可以使用Docker轻松地创建和管理多个运行环境,从而简化开发、测试和部署流程。此外,Docker还可以用来打包应用程序、构建基础设施、部署微服务和容器化应用程序。