蒙特卡洛树搜索（Monte Carlo Tree Search）揭秘

一. 什么是蒙特卡洛树搜索

蒙特卡洛树搜索(MCTS)是一种启发式搜索算法，一般用在棋牌游戏中，如围棋、西洋棋、象棋、黑白棋、德州扑克等。MCTS与人工神经网络结合，可发挥巨大的作用，典型的例子是2016年的AlphaGo，以4:1的比分战胜了韩国的9段棋手李世石。

二. 蒙特卡洛树搜索与蒙特卡罗方法的区别

蒙特卡罗方法使用随机抽样来解决其他方法难以或不可能解决的确定性问题，是一类计算方法的统称。它被广泛用在数学、物理的问题中，基本上能解决具有概率解释的任何问题。蒙特卡罗方法的应用领域包括：统计物理学、工程学、计算生物学、计算机图形学、AI游戏、金融和商业等。而蒙特卡洛树搜索(MCTS)就是其在AI游戏中的应用，它用于搜索游戏中的最佳动作。

三. MCTS的工作原理

MCTS使用一个tree来记录搜索结果，它更新tree的方法就是模拟游戏。就像人类在下棋时会在大脑中模拟对手的着法，厉害的甚至计算10步、20步以后，MCTS也是类似的原理。它先模拟几次游戏，然后把游戏结果记录在tree中，再根据最好的模拟结果选择最佳的动作。

MCTS一共包含4个步骤：选择（Selection）、扩展（Expansion）、模拟（Simulation）、反向传播（BackPropagation）。

1）选择（Selection）是从根节点开始，连续选择子节点，一直到达某个叶子节点，然后在那个节点上进行更新。也就是说，select时只会选leaf node（叶子节点）。

注意：根节点是当前的游戏状态，叶节点是尚未启动模拟的任何潜在子节点。

2）扩展（Expansion）也叫expand，是指一个节点往下，产生新的子节点。

3）模拟（Simulation）也叫rollout，是随机模拟，即以目前的状态开始，模拟一场游戏直到结束。有时也叫播放或推出。

expand和rollout区别是，如果目前节点是全新的，就进行rollout，如果节点已经被更新过，就进行expand。（这种说法可能不准确！）

4）反向传播（BackPropagation）就是把leaf node的更新一直往上传，直到根节点。有点类似神经网络的BP，但更简单，不涉及微积分。

MCTS整个执行过程如下

第一次模拟

我们有一个node，记录wi和ni的值，其中wi代表赢了几场，ni代表总场数。对于围棋来说，我们一般用wi代表黑棋赢的场数。

在一开始，我们没进行任何游戏，因此wi和ni都为0

第一步，选择一个没有child的node，目前只有root节点可选。

第二步，因为是全新的节点，需要进行rollout。由于root代表开局状态，黑棋和白棋都没下过，所以进行rollout没任何意义，因此先进行expand。在19x19的棋盘上，一共361个位置可以下。因此expand之后有361个child节点。

为了简单起见，假设只有两个位置可以选。

在expand之后，黑色root节点不再是leaf节点。

第三步，选择一个leaf节点进行rollout。从root开始寻找，此时有两个child选项。如何决定选哪个？这时候要用到一个概念，叫做UCB1(Upper Confidence Bound)，也叫上置信度边界1。如下

其中wi表示当前node赢的次数；ni表示当前node总共的模拟次数；Ni表示当前node的父节点的模拟次数；C是可以自己调整的参数，最常用的是 $\sqrt{2}$

对于左下角的leaf节点，还没模拟过，因此wi=0，ni=0，它的父节点即root，也是0/0，因此Ni=0，所以套用ucb1公式发现，分母为0无法计算。所以当做ucb1的结果无限大。同样右下角的节点也是无限大。

由于两个都是无限大，所以按顺序选节点即可，比如选择左下角节点。

此节点是leaf node，同时也是全新的节点，现在对它rollout。因为root节点代表黑棋下，所以现在轮到白棋下，然后黑棋再下，一直到游戏结束。

假设下到最后，黑棋赢了，那就更新这个node的值。因为黑棋赢了一场，就将wi更新为1，ni也更新为1.

接下来进行最后一步，即反向传播。因此黑色root节点也变为了1/1，如下

此时完成了一次MCTS模拟。一共需要几次模拟，是你可以自行设置的。模拟越多次，MCTS最后搜索的结果越准确，提供的着法越强大。一般需要跑几万几十万次甚至更多。这个例子，我们再进行几次更新说明。

第二次模拟

第一步，选择一个没有child的node，有两个选项，需要计算两个node的ucb1

左边的ucb1是1（代入公式可得），右边的ucb1是无穷大，右边更大，选择它。

第二步，因为是全新的节点，需要进行rollout（无需expand）。假设这次黑棋输了，如下

此时wi不会增加，仍为0，但是ni加1，于是有

第三步，反向传播。把黑色root节点的ni也加1，即有

第三次模拟

第一步，选择一个没有child的node，有两个选项，需要计算两个node的ucb1

左边是2.177，右边是1.177，因此选择左边。

第二步，因为该leaf节点已经被更新过，所以先expand。同样假设生成两个子节点。此时白色节点不再是leaf node，需要继续往下select。和前面一样，两个children节点都是新的，ucb1都是无穷大，因此按顺序选左边那个。

第三步，对左下角leaf节点进行rollout。和前面一样，随机下到游戏结束为止。这次假设黑棋输了。

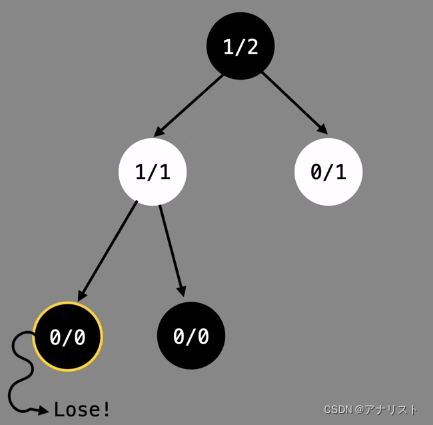
此时把ni更新为1，而wi保持不变。

第四步，反向传播。依次更新白色、黑色节点为1/2、1/3.

第四次模拟

第一步，选择一个没有child的node，第二层白色节点有两个，需要计算两个node的ucb1，左边是1.548，右边是1.482，左边更大选它。

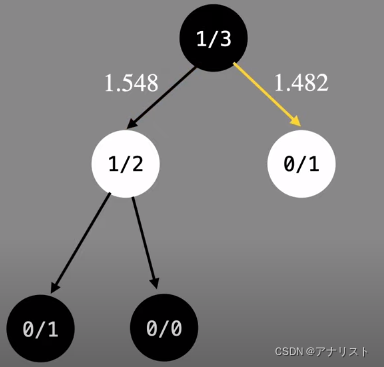
由于没到达leaf节点，需要继续往下select；此时轮到白的下，在计算ucb1的时候，要使用白棋的wi；而目前节点上记录的都是黑棋的胜率，需要进行换算；假设不考虑和棋（围棋的确没有和棋），白棋赢的次数=总场次-黑棋赢的次数；即ni-wi就是白棋赢的次数；所以左路径白棋的wi是1，得出ucb1为2.177；右路径白棋的wi是0，得出ucb1为无穷大；所以选择右边。

第二步，因为该leaf node是全新的节点，需要进行rollout（无需expand）。这次假设是黑棋赢，我们把wi和ni都加1，则0/0变为1/1

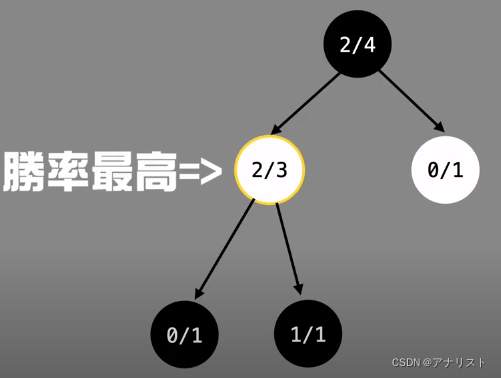
第三步，反向传播。白色节点、root节点依次变为2/3、2/4

四次模拟结束，你就可以决定该下哪步了。黑棋下左边的位置胜率为2/3，而右边胜率为0。所以下左边。

UCB1公式的意义

ucb1的公式分为左右两部分，左边是胜率，如果一个node的胜率越高，那么ucb1值也越高，即胜率越高的一步棋，越容易继续被选中。MCTS需要模拟足够多的次数，来让胜率越准确。

右边这一项，ni在分母，Ni在分子，因此模拟中一条路走过的次数越多，ni相对Ni就越大，就会导致ucb1相对变小。换言之，已经走过很多次的路，MCTS就不想再走了，这是为了探索其他路径会不会有更好的着法。

ucb1公式体现了游戏中平衡开发(exploitation)和探索(exploration)的思想。开发(exploitation)为了选择已知最好策略；探索(exploration)为了选择探索其他路线。如果只做exploitation，而忽略exploration，即永远选择胜率最高的路径，可能就无法发现更好的着法。如果只做exploration，而忽略exploitation，意味着对围棋361个位置进行平均的探索，会浪费很多时间探索胜率很低的路径，效率太差，MCTS的深度到不了太深，着法也不会准确。

四. AlphaGo如何使用MCTS

AlphaGo如何将MCTS和deep learning相结合的呢？

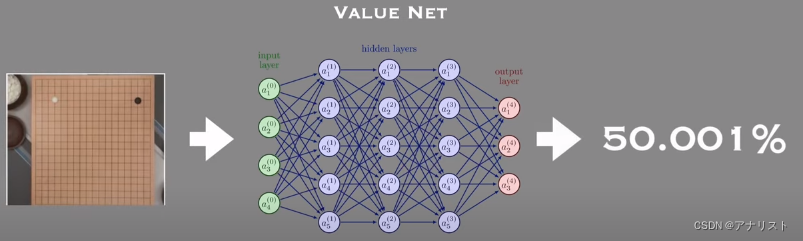
AlphaGo在搜索的时候，使用了两个神经网络，value network(值网络)和policy network(策略网络)，如下

policy network作用和原理：只要喂给policy network目前棋盘上的状态，它就可以得出下一步的最佳落点；policy network能给棋盘每个位置打分来选择下一步(即move)，这样就能取代ucb1；能减小search的广度(breadth)，并提高准确性

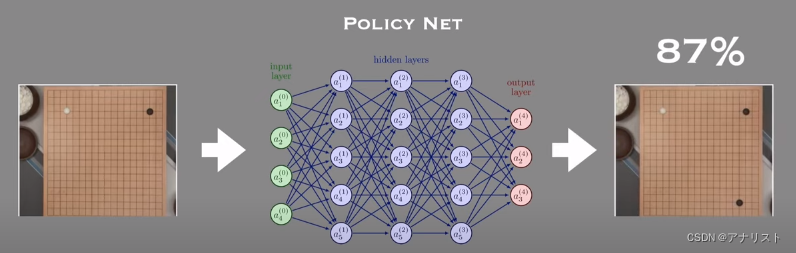
value network作用和原理：value network用来取代rollout，意思是不需要真正模拟到分出胜负。用value network就能根据棋局状态(即board positions)得出双方输赢的概率；能减小search的深度(depth)，并提高准确性

说明：AlphaGo的policy network有两种， supervised learning (SL) policy network和reinforcement learning (RL) policy network，即基于监督学习的策略网络和基于强化学习的策略网络，区别是训练数据来源的不同。SL的数据来自人类专家棋谱数据。RL的数据来自AI自我博弈(selfplay)。

policy network和value network的训练过程

policy network首先在人类专家数据上进行监督学习，从而能预测人类专家的着法；然后利用policy-gradient强化学习算法进行优化。value network利用两个训练好的policy network相互博弈来进行预测输赢。

扩展：AlphaGo、AlphaGo Zero和AlphaGo Master三者区别

AlphaGo Zero是只基于自我博弈(selfplay)强化学习训练得到的，没有任何人类数据的监督。AlphaGo Zero使用了单个neural network，而不是分开的policy network和value network两个网络。如果说AlphaGo中MonteCarlo rollout和value network同时存在，互相补充，那么在AlphaGo Zero中rollout则被neural network完全取代了。AlphaGo Zero的MCTS更加简化。AlphaGo Master和AlphaGo Zero使用的算法和模型一样，但使用了部分人类专家数据。

五. MCTS的优缺点

MCTS能够非常聪明的去探索胜率较高的路径，和dfs这类暴力穷举算法比起来，可以花费较少的运算资源，就能达到不错的效果，尤其对于围棋这类每步棋都有200种左右选择的游戏，使用MCTS的效果非常显著。但与此同时也要指出，MCTS并不能保证一定找到最佳路径和着法。AlphaGo和李世石比赛就输了一盘，说明不一定能百分百找到最优解。不过论整体胜率，AlphaGo和AlphaGo Zero已远远超过了人类。既然围棋的变化(10的360次方)比宇宙中的原子还多，比起dfs或minimax等算法，使用MCTS还是非常有优势和有必要的。