1. 题目链接:695. 岛屿的最大面积
2. 题目描述:
给你一个大小为
m x n的二进制矩阵grid。岛屿 是由一些相邻的
1(代表土地) 构成的组合,这里的「相邻」要求两个1必须在 水平或者竖直的四个方向上 相邻。你可以假设grid的四个边缘都被0(代表水)包围着。岛屿的面积是岛上值为
1的单元格的数目。计算并返回
grid中最大的岛屿面积。如果没有岛屿,则返回面积为0。示例 1:
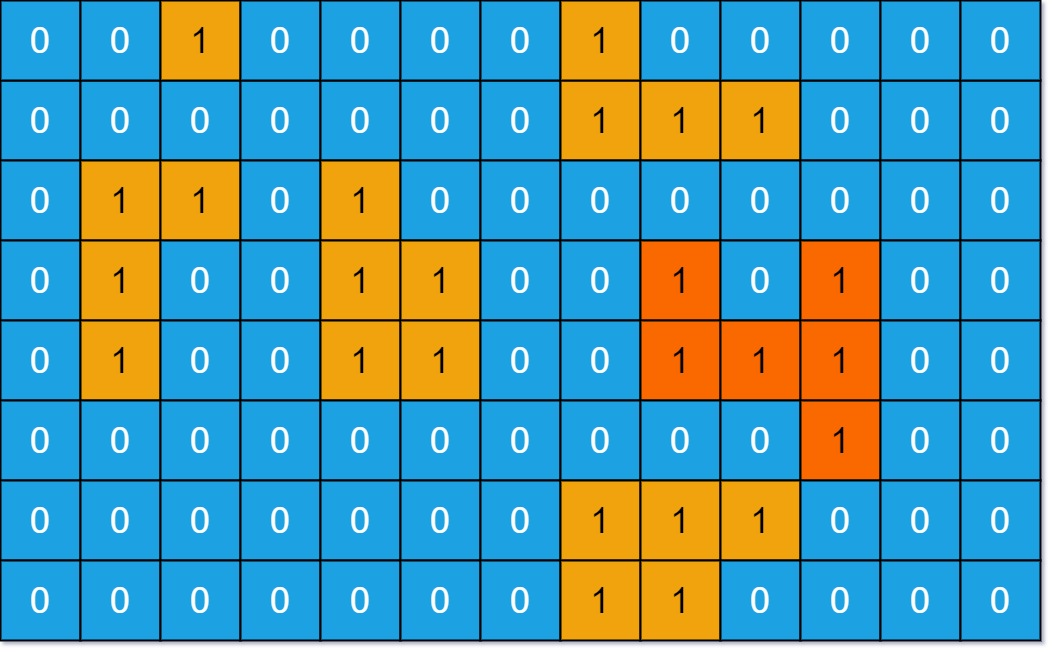
输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]] 输出:6 解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。示例 2:
输入:grid = [[0,0,0,0,0,0,0,0]] 输出:0提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 50grid[i][j]为0或1,
3. 解法(递归):
3.1 算法思路:
- 遍历整个矩阵,每当遇到一块土地的时候,就用深度优先遍历或者宽度优先遍历将与这块土地相连的整个岛屿的面积计算出出来
- 然后在搜索得到的所有岛屿面积求一个最大值即可
- 在搜索过程中,为了防止搜到重复的土地:
- 可以开一个同等规模的布尔数组,标记以下这个位置是否已经被访问过
- 也可以将原始矩阵的
1修改成0,但是这样的操作会修改原始矩阵
3.2 算法流程:
主函数内:
- 遍历整个数组,发现一块没有遍历到的土地之后,就用
dfs将于这块土地相连的岛屿的面积求出来 - 然后将面积更新到最终结果
ret中
深度搜索dfs中:
- 能够进到
dfs函数中,说明是一个没遍历到的位置 - 标记一下已经遍历过,设置一个变量
count,记录最终的面积 - 上下左右遍历四个位置:如果找到一块没有遍历到的土地,就将这块土地相连的岛屿面积累加到
count上 - 循环结束后,
count中存的就是这块岛屿的面积,返回即可
3.3 C++算法代码:
class Solution {bool vis[51][51]; // 访问标记数组,用于记录某个位置是否已经访问过int m, n; // 网格的行数和列数int dx[4] = {0, 0, 1, -1}; // x轴方向的偏移量int dy[4] = {1, -1, 0, 0}; // y轴方向的偏移量int count; // 当前岛屿的面积
public:// 计算给定网格中最大的岛屿面积int maxAreaOfIsland(vector<vector<int>>& grid) {m = grid.size(), n = grid[0].size();int ret = 0; // 最大岛屿面积for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (!vis[i][j] && grid[i][j] == 1) { // 如果当前位置未被访问且为陆地count = 0; // 重置岛屿面积dfs(grid, i, j); // 进行深度优先搜索ret = max(ret, count); // 更新最大岛屿面积}}}return ret; // 返回最大岛屿面积}// 深度优先搜索函数,用于计算岛屿面积void dfs(vector<vector<int>>& grid, int i, int j) {count++; // 当前位置为陆地,岛屿面积加一vis[i][j] = true; // 标记当前位置已访问for (int k = 0; k < 4; k++) { // 遍历四个方向int x = i + dx[k], y = j + dy[k]; // 计算下一个位置的坐标if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && grid[x][y] == 1) { // 如果下一个位置在网格范围内且未被访问且为陆地dfs(grid, x, y); // 继续深度优先搜索}}}
};
![[Mac软件]Adobe XD(Experience Design) v57.1.12.2一个功能强大的原型设计软件](https://img-blog.csdnimg.cn/90aa798e3f794ba2a93e298844537ba1.png)