1.1 概率论内容介绍

1.1.1 概率论介绍

概率论是研究随机现象数量规律的数学分支。随机现象是相对于决定性现象而言的，在一定条件下必然发生某一结果的现象称为 决定性现象 。

概率论是用来描述不确定性的数学工具，很多数据挖掘中的算法都是通过描述样本的概率相关信息或推断来构建模型。

1.1.2 实验介绍

本章节主要实现概率与统计相关的知识点，主要用到的框架是 numpy 和 scipy 框架。

1.2 概率论内容实现

导入相应库：

import numpy as np 
import scipy as sp 

1.2.1 均值实现

数据准备：

ll = [[1,2,3,4,5,6],[3,4,5,6,7,8]]

代码输入：

np.mean(ll) 	#全部元素求均值

结果输出：

4.5

np.mean(ll,0) #按列求均值，0代表列向量

结果输出：

array([2., 3., 4., 5., 6., 7.])

np.mean(ll,1)	#按行求均值，1表示行向量

结果输出：

array([3.5, 5.5])

1.2.2 方差实现

数据准备:

b=[1,3,5,6]
ll=[[1,2,3,4,5,6],[3,4,5,6,7,8]]

求方差（variance）：

np.var(b)

结果输出：

3.6875

代码输入：

np.var(ll,1)	#第二个参数为1，表示按行求方差

结果输出：

[2.91666667 2.91666667]

解释：按行求方差，所以可以将ll拆开来计算也是可以得到一样的结果的

aa = [1,2,3,4,5,6]
np.var(aa)
bb = [3,4,5,6,7,8]
np.var(bb)

得到的结果都是 2.9166666666666665 ，保留8位小数点，则是2.91666667。

自行实践：

ttt,ddd = np.var(ll,1)
print(ttt, ddd)

思考：为什么aa与bb的方差都是一样的？

方差的意义：方差反映了一组数据与其平均值的偏离程度。 通常用方差来衡量一组数据的稳定性，方差越大，波动性越大；方差越小，波动性越小，也就越稳定。很明显，aa的平均值是3.5，bb的平均值是5.5，两者与其平均值的偏离程度是一样的，所以两者的方差一样。

注意：平均值相同，并不代表着方差相同。如：

aaa=[0,5,9,14]
bbb=[5,6,8,9]

两者的平均值都是7，但是方差却不相同，凭直觉上说，很明显aaa的元素偏离7要大一些，所以，凭直觉也是可以知道aaa的方差要比bbb的更大一些。

1.2.3 标准差实现

数据准备:

ll=[[1,2,3,4,5,6],[3,4,5,6,7,8]]

代码输入：

np.std(ll)

结果输出：

1.9790570145063195

补充：标准差也称为均方差，标准差是方差的算术平方根。

思考：为什么有了方差还有有标准差？
其实简单一句话解释就是，让计算结果不要与其自身的元素相差太大（单位一致）。

比如：

aaa=[0,5,9,14]
np.var(aaa)

计算结果是 26.5 ，可以发现，经过一个平方后，其方差的值26.5与其自身的元素（0,5,9,14）其实相差比较大了，我们可以再开个方根回来，让其值于原来的元素不要相差那么大，保持数据的单位一致。实际上np.std(aaa)的计算结果是 5.1478150704935 。

尝试： aaa=[0,50,90,140] ，请计算方差与标准差。

参考解释：有了方差为什么需要标准差？

1.2.4 协方差实现

数据准备:

b=[1,3,5,6]

代码输入：

np.cov(b)

结果输出：

4.916666666666666

补充： 协方差 （Covariance）在概率论和统计学中用于衡量 两个变量 的总体误差。而 方差 是协方差的一种特殊情况，即当 两个变量是相同 的情况。

说明：

b=[5,5]
np.cov(b)
np.std(b)

输出结果是一样的！b=[5,5,5,5,5]也是一样的。

1.2.5 相关系数

数据准备:

vc=[1,2,39,0,8]
vb=[1,2,38,0,8]

利用函数实现：

np.corrcoef(vc,vb)

结果输出：

array([[1.        , 0.99998623],[0.99998623, 1.        ]])

解释：输出结果是一个2x2的NumPy数组，表示两个变量 vc 和 vb 之间的相关系数矩阵。相关系数矩阵是一个对称矩阵，其中对角线上的元素是各自变量与自身的相关系数，而非对角线上的元素是两个不同变量之间的相关系数。

• 1.0 ：对角线上的元素表示每个变量与自身的相关系数。由于变量与自身完全相关，所以相关系数为1.0。

• 0.99998623 ：非对角线上的元素表示两个不同变量之间的相关系数。在这种情况下，vc 和 vb 之间的相关系数非常接近1.0，约为0.99998623。这表明这两个变量之间存在着极强的正线性相关性。

相关系数矩阵的结果表明变量 vc 和 vb 之间具有非常强的正线性相关性，即当一个变量增加时，另一个变量也会增加，且变化趋势非常相似。相关系数接近1.0表示它们之间的线性关系非常密切。

补充：coordination（协调、配合、协作）、 coefficient（系数）

1.2.6 二项分布实现

服从二项分布的随机变量X表示在n次独立同分布的伯努利试验中成功的次数，其中每次试验的成功概率为p。

from scipy.stats import binom, norm, beta, expon
import numpy as np
import matplotlib.pyplot as plt#n,p对应二项式公式中的事件成功次数及其概率，size表示采样次数
binom_sim = binom.rvs(n=10, p=0.3, size=10000)
print('Data:',binom_sim)
print('Mean: %g' % np.mean(binom_sim))
print('SD: %g' % np.std(binom_sim, ddof=1))
#生成直方图，x指定每个bin(箱子)分布的数据,对应x轴，binx是总共有几条条状图，density值密度,也就是每个条状图的占比例比,默认为1
plt.hist(binom_sim, bins=10, density=True)
plt.xlabel(('x'))
plt.ylabel('density')
plt.show()

说明：旧版本是使用normed表示值密度，新版本是用density，直接替换即可，效果一样。

结果输出：

Data: [2 2 4 ... 1 4 2]
Mean: 2.9918
SD: 1.4365

二项分布图如下：

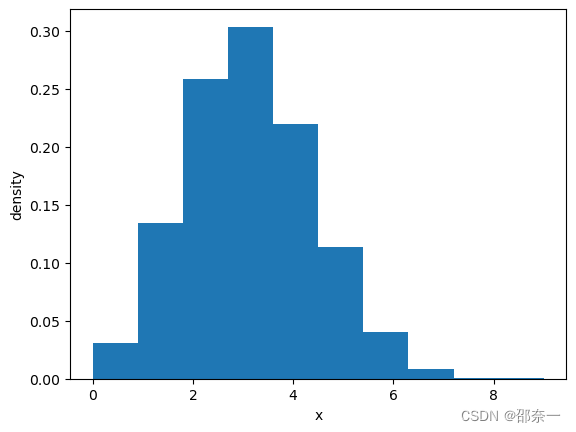
1.2.7 泊松分布实现

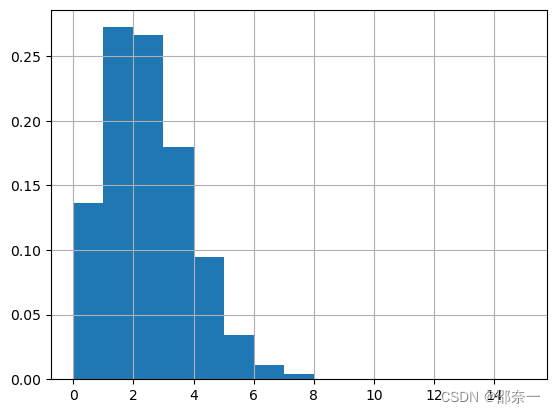
一个服从泊松分布的随机变量X，表示在具有比率参数λ的一段固定时间间隔内，事件发生的次数。参数λ告诉你该事件发生的比率。随机变量X的平均值和方差都是λ。

import numpy as np
import matplotlib.pyplot as plt#产生10000个符合lambda=2的泊松分布的数
X= np.random.poisson(lam=2, size=10000)  
a = plt.hist(X, bins=15, density=True, range=[0, 15])#生成网格
plt.grid()
plt.show()

泊松分布图如下：

1.2.8 正态分布

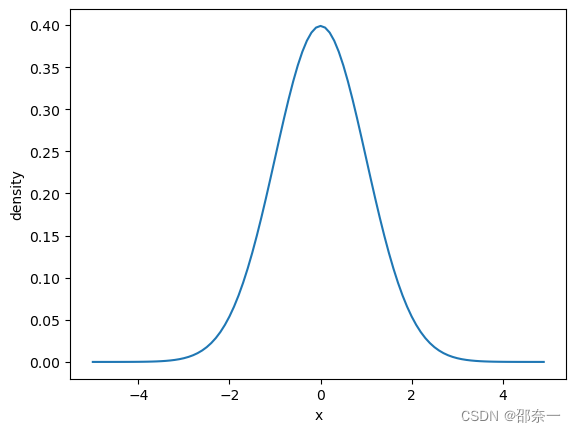
正态分布 是一种连续分布，其函数可以在实线上的任何地方取值。正态分布由两个参数描述：分布的平均值μ和标准差σ 。

from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as pltmu = 0
sigma = 1#分布采样点
x = np.arange(-5, 5, 0.1)
#生成符合mu,sigma的正态分布
y = norm.pdf(x, mu, sigma)
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('density')
plt.show()

分布图如下：

1.2.9 指数分布

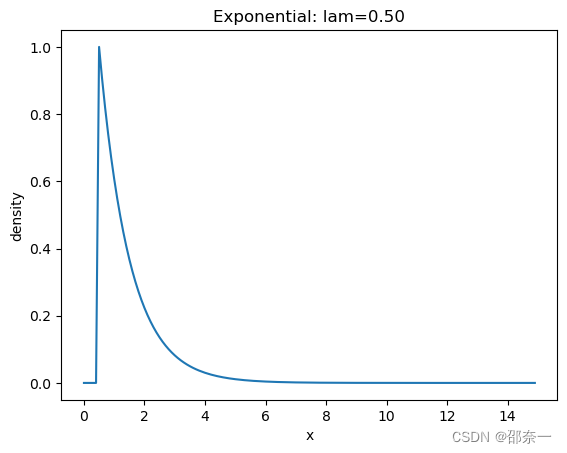
指数分布是一种连续概率分布，用于表示独立随机事件发生的时间间隔。比如旅客进入机场的时间间隔、打进客服中心电话的时间间隔等。

from scipy.stats import expon
import numpy as np
import matplotlib.pyplot as pltlam = 0.5
#分布采样点
x = np.arange(0, 15, 0.1)
#生成符合lambda为0.5的指数分布
y = expon.pdf(x, lam)
plt.plot(x, y)
plt.title('Exponential: lam=%.2f' % lam)
plt.xlabel('x')
plt.ylabel('density')
plt.show()

分布图如下：

1.2.10 中心极限定理的验证

中心极限定理证明了一系列相互独立的随机变量的和的极限分布为正态分布。即使总体本身不服从正态分布，只要样本组数足够多即可让中心极限定理发挥作用。此实验用于验证中心极限定理。

生成数据。假设观测一个人掷骰子，掷出1~6的概率都是相同的：1/6。掷了一万次。

import numpy as np
import matplotlib.pyplot as plt
#随机产生10000个范围为(1,6)的数
ramdon_data = np.random.randint(1,7,10000)
print(ramdon_data.mean())
print(ramdon_data.std())

输出结果：

3.4821
1.7102279351010499

生成直方图：

plt.figure()
plt.hist(ramdon_data,bins=6,facecolor='blue')
plt.xlabel('x')
plt.ylabel('n')
plt.show()

分布图如下：

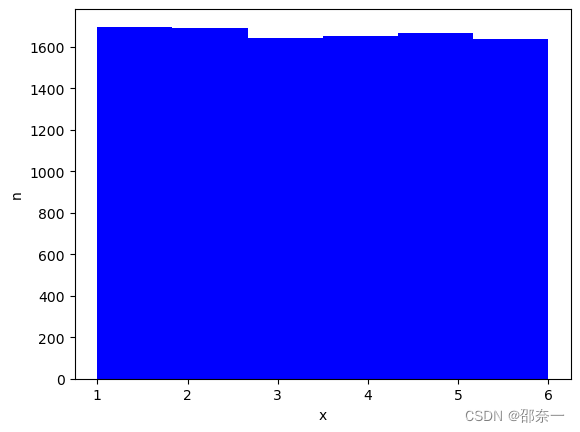
图解：投掷1万次，掷出1-6的次数相差无几。

随机抽取10个数据：

sample1 = []#从生成的1000个数中随机抽取10个
for i in range(1,10):# int(np.random.random()*len(ramdon_data))为随机生成范围为(0,10000)的整数sample1.append(ramdon_data[int(np.random.random()*len(ramdon_data))])sample1 = np.array(sample1)
print(sample1)
print(sample1.mean())
print(sample1.std())

输出如下：

[2 1 3 2 2 2 3 5 1]
2.3333333333333335
1.1547005383792515

随机抽取1000组数据，每组50个：

samples = []
samples_mean =[]
samples_std = []#从生成的1000个数中随机抽取1000组
for i in range(0,1000):sample = []#每组随机抽取50个数for j in range(0,50):sample.append(ramdon_data[int(np.random.random() * len(ramdon_data))])#将这50个数组成一个array放入samples列表中sample_ar = np.array(sample)samples.append(sample_ar)#保存每50个数的均值和标准差samples_mean.append(sample_ar.mean())
samples_std.append(sample_ar.std())
#samples_std_ar = np.array(samples_std)
#samples_mean_ar = np.array(samples_mean)
#print(samples_mean_ar)

生成直方图：

plt.figure()
#根据抽取的1000数据的均值，生成直方图，10个条形柱，柱的颜色为蓝色
plt.hist(samples_mean,bins=10,facecolor='blue')
plt.xlabel('x')
plt.ylabel('n')
plt.show()

分布图如下：

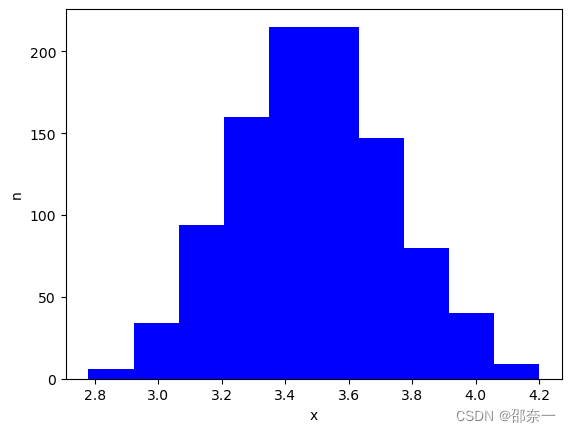
图解：相互独立的随机变量的和的极限分布为正态分布