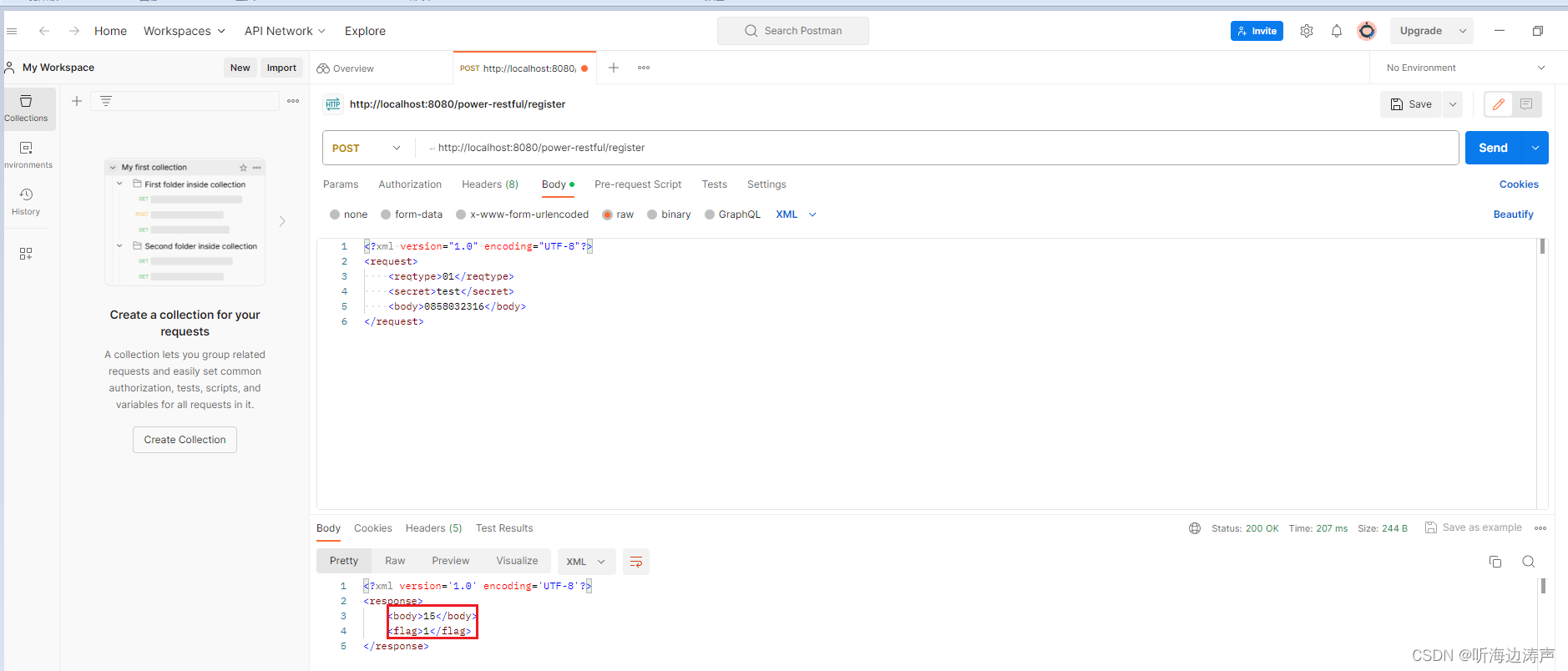
一、介绍
在这篇文章中,我们将重点介绍 Transformer 背后的 Scaled Dot-Product Attention,并详细解释其计算逻辑和设计原理。
在文章的最后,我们还会提供一个Attention的使用示例,希望读者看完后能够对Attention有更全面的了解。
二、缩放点积注意力
现在我们已经了解了注意力机制的原型,但是它未能解决输入处理速度慢的问题。为了提高计算速度并利用并行计算的能力,有必要放弃传统的一次处理一个字符的方法。
论文《Attention Is All You Need》引入了Scaled Dot-Product Attention来克服这一挑战。公式如下:
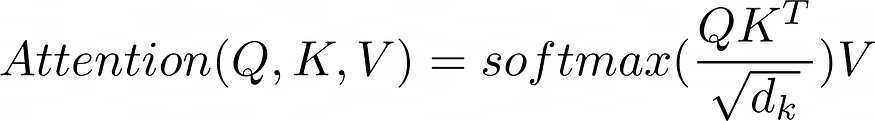
该公式可能看起来很复杂,但可以分解为更简单的步骤。让我们探索每个步骤以了解其背后的原理。
1.QKᵀ
在此步骤中,我们使用两个矩阵:Q(查询)和 K(键)。假设Q有3条数据,K有4条数据。两个矩阵的维数分别为3 * dₖ和4 * dₖ。
需要注意的是,两个矩阵需要具有相同的列数。解释是:
- Q 有 3 条数据,每条数据由一个长度为 dₖ 的向量表示。
- K有四条数据,每条数据由一个长度为dₖ的向量表示。
如果用于表示 Q 和 K 的输入序列的维度不相同,或者想要指定特殊的 dₖ,则可以使用 和 将Linear(input_q_dim, dₖ)原始Linear(input_k_dim, dₖ)Query 和 Key 线性变换为 dₖ 维度。
这两层的目的是将两个序列变换到相同的向量空间。


现在我们有了 Q 和 K 矩阵(假设 dₖ = 4),让我们仔细看看 QKᵀ 正在做什么。

该动画演示了查询矩阵和关键矩阵 QKᵀ 的乘积生成一个 3x4 矩阵。
此阶段对应于点积运算,因为结果矩阵的 (i, j) 项是Q 中的第 i 行和 K 中的第 j 行的点积,这也表示 Kⱼ 对 Qᵢ 的重要性。
总之,到目前为止,缩放点积注意力机制执行以下步骤:
- 它将输入查询和键映射到相同的向量空间,其中它们的内积为更相关的对带来更高的值(这种转换是由模型学习的)。
- 它通过获取查询矩阵和关键矩阵的内积来计算注意力表 A。
2.softmax(A /√dₖ)
该阶段对应于其名称中的Scaled部分。要理解这一步,首先了解 softmax 函数很重要。
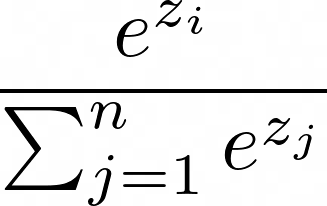
对于 A 中的每一行,softmax 函数将每个元素映射到 0 到 1 之间的值,使得每行中的值之和等于 1。
如果我们固定一个特定的坐标 zᵢ 并仅改变该值,同时保持向量中的其他元素不变,则生成的函数看起来类似于 sigmoid 曲线:
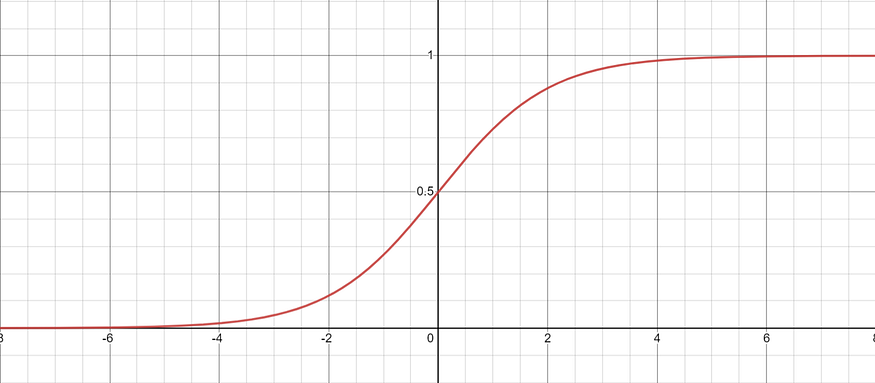
值得注意的是,softmax函数的梯度在极值处几乎为零,使得在训练期间更新相应参数变得困难。
如果将键向量和值向量的维度 dₖ 设置得很大,则注意力矩阵 A 中的点积分数更有可能落入这些区域,因为有 dₖ 项需要相乘和求和。
为了缓解这个问题,引入了缩放因子 √dₖ 来降低分数的大小并减少遇到梯度消失的机会。
该技术有助于提高模型在训练过程中的稳定性和收敛性。
我们将经过softmax的矩阵称为A'。
高级(可选):
假设查询向量和键向量中的每个元素都是从标准正态分布 N(0, 1) 独立采样的,根据下面的点积公式:
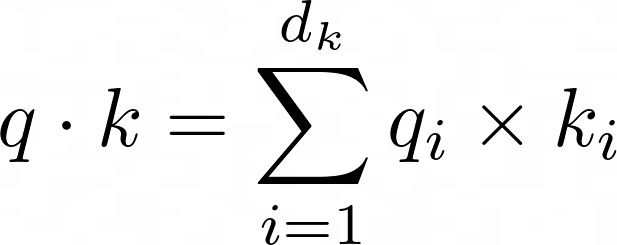
q 和 k 的点积服从均值为 0、方差为 dₖ 的正态分布。
将点积除以 √dₖ 将其缩放至方差为 1。
3. AV
在深入研究本节之前,让我们回顾一下 A' 的属性:
- A' 的行数与输入查询的数量相同。
- A' 的列数与输入键的数量相同。
- A' 的每一行中的每个元素都在 0 到 1 的范围内,其中 (i, j) 条目表示第 j 个键对于第 i 个查询的重要性。
- A' 的单行中所有元素的总和等于 1。
假设 A' 看起来像这样:

接下来,我们讨论 V,它代表键背后的实际值。
您可以将键视为学生 ID,将值视为姓名、班级和成绩等信息。你用学生证来找人,但相关信息才是其背后的价值。对于模型来说,也是一样的:这些值是它实际用来计算的值。
V的维度由dᵥ表示,可以设置为任何合适的值。您还可以使用Linear(input_k_dim, dᵥ)将输入向量转换为该维度。
注意,我将上述命令的第一个参数设置为input_k_dim,这是因为键和值的来源应该是相同的向量,但一个转换为 Q 的空间进行比较,另一个转换为实际值。
也就是说,键和值是一一对应的,第一个值对应第一个键,第二个值对应第二个键,以此类推。
V的外观是这样的:

让我们看看 A'V 做了什么:

从上式中,我们可以观察到 A'V 将:
- 生成一个矩阵,其中行数等于查询数。
- 对于每个查询,其最终值是 V 中行的加权平均值。
- 权重基于查询及其相应键的内积。
三、缩放点积注意力的结论
事实上,有两件事正在做:
- 创建查找表(Q 和 K 的内积、缩放、softmax)。
- 根据注意力表对 V 中的行进行加权平均,计算最终输出。
你也可以把键和值想象成一种数据库,注意力实际上就是根据数据库中的内容找到一个合适的向量来表示每个查询。
在前面的解释中,Query和Key-Value是两个不同的序列,但实际上,它们的输入可以是相同的序列,这种情况称为Self-Attention。
自注意力在自然语言处理中特别有用,其中输出可以被视为考虑上下文的每个查询的词嵌入。
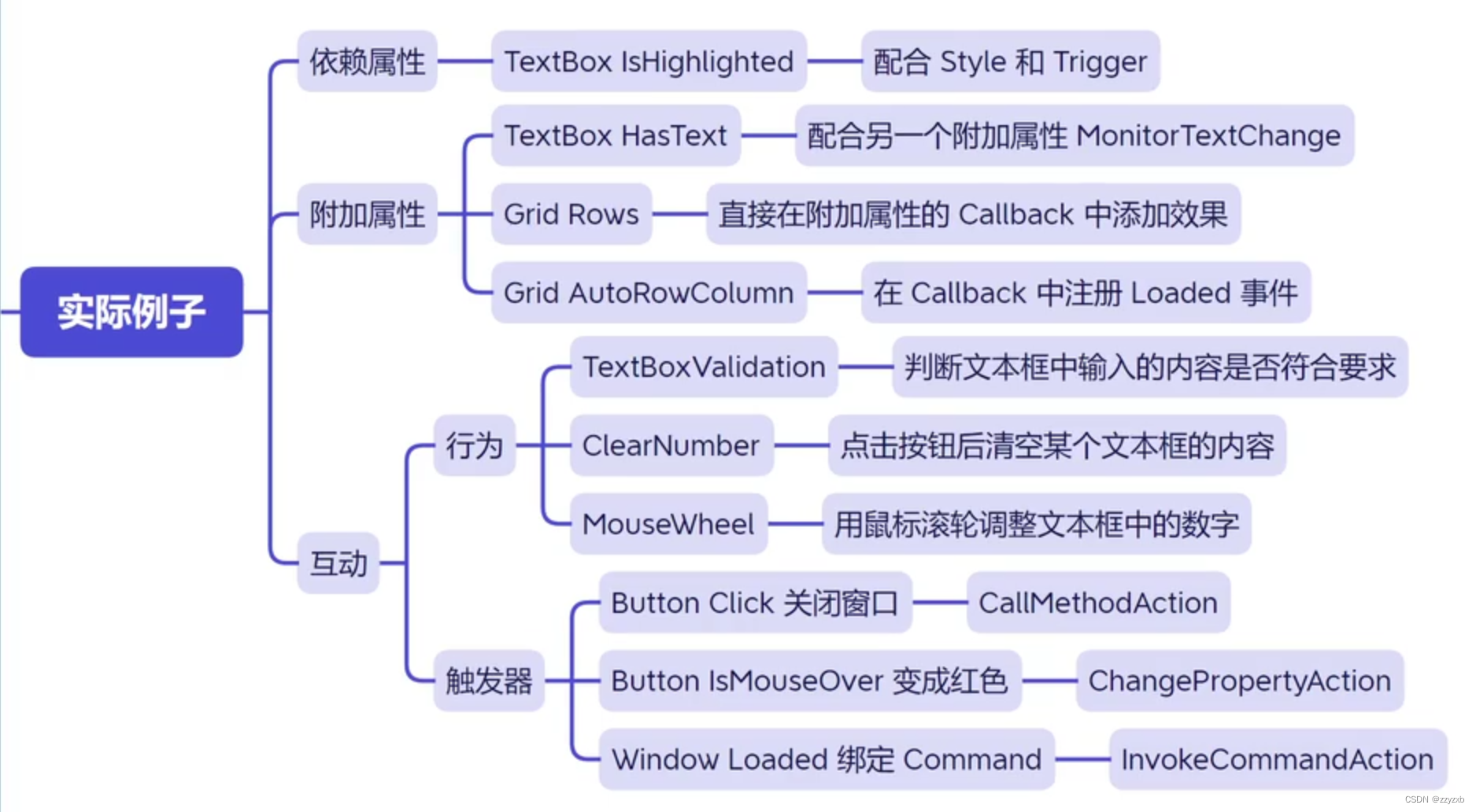
四、例子
最后,提供了一个使用注意力的实际例子来加深您的理解。假设我们要将计算机科学系和哲学系(两个查询)转换为模型可以理解的向量,并且数据库中有四个科目(四个键值对):英语、社会研究、数学、和物理。模型计算出的注意力表可能如下所示:
![]()
解读如下:对于XX系来说,这四门科目的重要性是……

接下来,我们需要V的值。这里,我设置dᵥ = 3,其中V中的三个值分别代表记忆力、语言能力和逻辑推理能力。
(注意:实际上,我们无法知道 Value 的列代表什么,模型会自己找出它们应该代表什么。)
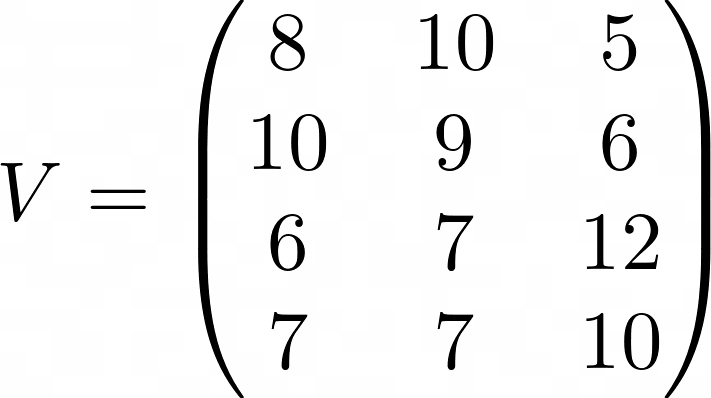
解读如下:对于XX科目,要做好的记忆力、语言、逻辑推理成绩分别是……

(分数纯属虚构。)
两个矩阵相乘:
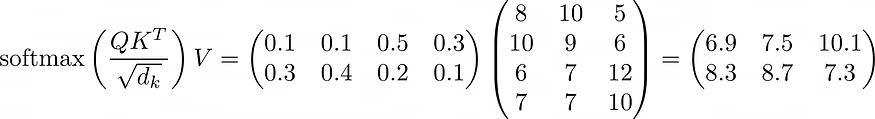
最终结果如下:在XX系取得好成绩所需的记忆力、语言力、逻辑推理分数分别为……

该模型还将使用两个向量6.9 7.5 10.1和8.3 8.7 7.3分别代表两个部门。
我希望这个例子能让你清楚地理解注意力是如何运作的以及如何建立注意力维度。
五、结论
本文详细介绍了Scaled Dot-Product Attention的计算细节和设计逻辑,以及Attention的使用示例。如果我们仔细对比上一篇文章介绍的模型,我们会发现,虽然两种架构看起来差别很大,但整体逻辑却相当相似。
除了注意力之外,Transformer 架构还包含其他几个关键元素,例如编码器和解码器结构、MultiHead 和位置编码。尽管本文无法深入讨论这些方面,但我们希望在以后的文章中更详细地探讨它们。