1、寻找 左边 / 右边 距离当前元素最近的 更小 元素的 下标
1.1 leetcode 84:柱状图中最大的矩形
第一遍代码思路错了,如:输入[2,1,2],对于2,因为比栈顶元素1大,然后就会直接得出2(1,2),但是其实之前那个1也是可以用的,如果使用2,1,2就会得出3
错误思路:
单调栈内从栈顶到栈底 递增,因为除非加入的元素本身比所有可能的最大矩阵还大,不然后续计算就不需要管比栈顶元素大的元素
当加入的元素比栈顶大的时候:要比较自己的大小,之前最大矩阵的大小 和 与栈顶元素组成新的矩阵与最大矩阵加上自己后的大小,再考虑入不入栈
如果碰到等于栈顶元素的,直接不用入栈,因为对矩阵的高度不会产生影响,直接加一个栈顶元素即可
如果碰到小于栈顶元素的,比较自己加入后有没有使最大矩阵变大(高度变低长度加一),有就入栈更新最大矩阵,没有直接不入
碰到小于栈顶元素的情况:比较自己加入后有没有使最大矩阵变大(高度变低长度加一),有就更新最大矩阵,有或者没有都直接入栈
但是发现对于栈内从栈顶到栈底递增的单调栈来说,没有办法计算加入之后的矩阵,因为不知道上一个比自己小的元素是谁
再构建一个从栈顶到栈底单调递减的栈,这个栈单纯找到左边第一个更小的元素的下标即可
if(res == mat1) 加入的元素本身比所有可能的最大矩阵还大,直接清空栈加入这个元素
class Solution {
public:int largestRectangleArea(vector<int>& heights) {/*单调栈内从栈顶到栈底 递增,因为除非加入的元素本身比所有可能的最大矩阵还大,不然后续计算就不需要管比栈顶元素大的元素当加入的元素比栈顶大的时候:要比较自己的大小,之前最大矩阵的大小 和 与栈顶元素组成新的矩阵与最大矩阵加上自己后的大小,再考虑入不入栈如果碰到等于栈顶元素的,直接不用入栈,因为对矩阵的高度不会产生影响,直接加一个栈顶元素即可如果碰到小于栈顶元素的,比较自己加入后有没有使最大矩阵变大(高度变低长度加一),有就入栈更新最大矩阵,没有直接不入*/if(heights.size() == 0) return 0;int res = heights[0];stack<int> st;st.push(0);stack<int> st2;//栈顶到栈底递减 单调栈st2.push(heights.size() - 1);vector<int> getMin(heights.size(), -1);//找左边更小元素的下标for(int i = heights.size() - 2; i >= 0; i--) {while(!st2.empty() && heights[i] < heights[st2.top()]) {getMin[st2.top()] = i;st2.pop();}st2.push(i);}for(int i = 1; i < heights.size(); i++) {if(heights[i] == heights[st.top()]) {res += heights[i];}else if(heights[i] > heights[st.top()]) {int mat1 = heights[i];int mat2 = res;int mat3 = heights[st.top()] * (i - st.top() + 1);res = max(mat1, max(mat2, mat3));if(res == mat1) {//加入的元素本身比所有可能的最大矩阵还大,直接清空栈加入这个元素while(!st.empty()) {st.pop();}st.push(i);}}else {st.push(i);/*比较自己加入后有没有使最大矩阵变大(高度变低长度加一),有就更新最大矩阵,有或者没有都直接入栈但是发现对于栈内从栈顶到栈底递增的单调栈来说,没有办法计算加入之后的矩阵,因为不知道上一个比自己小的元素是谁再构建一个从栈顶到栈底单调递减的栈,这个栈单纯找到左边第一个更小的元素的下标即可*/int mat = 0;if(getMin[st.top()] == -1) {mat = heights[i] * (i + 1);}else {mat = heights[i] * (i - getMin[st.top()]);}if(res < mat) {res = mat;}}}return res;}
};1.2 leetcode 84:暴力解法
其实跟昨天 leetcode 42:接雨水 思路差不多都是左右找元素,不同的是找到 左边 / 右边 第一个 更小的 元素,矩阵的高是由当前元素决定的(最高的),宽度是右边减左边减一即可
然后把矩阵中最大的那个记录就行
class Solution {
public:int largestRectangleArea(vector<int>& heights) {int sum = 0;for (int i = 0; i < heights.size(); i++) {int left = i;int right = i;for (; left >= 0; left--) {if (heights[left] < heights[i]) break;}for (; right < heights.size(); right++) {if (heights[right] < heights[i]) break;}int w = right - left - 1;int h = heights[i];sum = max(sum, w * h);}return sum;}
};
1.3 leetcode 84:双指针解法
根据思路写代码:
记录左边 第一个 更小的节点 下标:vector<int> leftMin(heights.size(), -1);
记录右边 第一个 更小的节点 下标:vector<int> rightMin(heights.size(), -1);
注意数组记录的是 下标 不是元素值
注意跟 leetcode 42:接雨水 不同,不是找左边最大值了,找最近的更小的值,所以不是用if,而是不断向左遍历更小元素。寻找的过程中,一旦小了就停,而且记录的是 下标 不是 数值大小
for(int i = 1; i < heights.size(); i++) {int t = i - 1;while(t >= 0 && heights[t] >= heights[i]) {t = leftMin[t];}leftMin[i] = t;
}
完整代码:
class Solution {
public:int largestRectangleArea(vector<int>& heights) {vector<int> leftMin(heights.size(), -1);//记录左边第一个更小的节点 下标vector<int> rightMin(heights.size(), -1);//记录右边第一个更小的节点 下标//注意数组记录的是下标不是元素值for(int i = 1; i < heights.size(); i++) {//注意跟 leetcode 42:接雨水 不同,不是找左边最小值了,找最近的更小的值,所以不是用if,而是不断向左遍历更小元素寻找的过程,一旦小了就停int t = i - 1;while(t >= 0 && heights[t] >= heights[i]) {t = leftMin[t];}leftMin[i] = t;}for(int i = heights.size() - 2; i >= 0; i--) {int t = i + 1;while(t < heights.size() && heights[t] >= heights[i]) {t = rightMin[t];}if(t < heights.size()) {rightMin[i] = t;}else {rightMin[i] = -1;}}int res = 0;for(int i = 0; i < heights.size(); i++) {int left = 0;if(leftMin[i] == -1) {left = -1;}else {left = leftMin[i];}int right = 0;if(rightMin[i] == -1) {right = heights.size();}else {right = rightMin[i];}int s = heights[i] * (right - left - 1);res = max(res, s);}return res;}
};
代码随想录思路及代码:
本题双指针的写法整体思路和 leetcode 42:接雨水 是一致的,但要比 leetcode 42:接雨水 难一些
难就难在本题要记录记录每个柱子 左边第一个 小于 该柱子的下标,而不是左边第一个小于该柱子的高度
所以需要循环查找,也就是下面在寻找的过程中使用了while
class Solution {
public:int largestRectangleArea(vector<int>& heights) {vector<int> minLeftIndex(heights.size());vector<int> minRightIndex(heights.size());int size = heights.size();// 记录每个柱子 左边第一个小于该柱子的下标minLeftIndex[0] = -1; // 注意这里初始化,防止下面while死循环for (int i = 1; i < size; i++) {int t = i - 1;// 这里不是用if,而是不断向左寻找的过程while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];minLeftIndex[i] = t;}// 记录每个柱子 右边第一个小于该柱子的下标minRightIndex[size - 1] = size; // 注意这里初始化,防止下面while死循环for (int i = size - 2; i >= 0; i--) {int t = i + 1;// 这里不是用if,而是不断向右寻找的过程while (t < size && heights[t] >= heights[i]) t = minRightIndex[t];minRightIndex[i] = t;}// 求和int result = 0;for (int i = 0; i < size; i++) {int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);result = max(sum, result);}return result;}
};
1.4 leetcode 84:单调栈
本题单调栈的解法和接雨水的题目是遥相呼应的
为什么这么说呢,leetcode 42:接雨水 是找每个柱子左右两边第一个大于该柱子高度的柱子,而本题是找每个柱子左右两边第一个小于该柱子的柱子
根据思路写代码报错:
class Solution {
public:int largestRectangleArea(vector<int>& heights) {//递减的单调栈,等发现当前元素大于栈顶元素,说明找到右边第一个更大的了int res = heights[0];stack<int> st; st.push(0);for(int i = 1; i < heights.size(); i++) {if(heights[i] >= heights[st.top()]) {st.push(i);}else {while (!st.empty() && heights[i] < heights[st.top()]) { int mid = st.top();st.pop();if (!st.empty()) {int left = st.top();int right = i;int w = right - left - 1;int h = heights[mid];res = max(res, w * h);}}st.push(i);}}//对于剩下的在栈内递减的元素的处理if(!st.empty()) {int rightIndex = st.top();while(st.size() > 1) {st.pop();}int leftIndex = st.top();int mat_s2 = heights[st.top()] * (rightIndex - leftIndex + 1);if(res < mat_s2) res = mat_s2;}return res;}
};
对剩下的在栈内的元素处理出了问题,因为不一定是最小的那个元素乘以长度就是最大,还可能是某几个连续元素画矩阵最大
还是在头尾加两个0元素靠谱,这样保证所有非0元素都可以被计算过
对于这段代码一开始没理解,说明之前暴力双指针的部分也没理解透:为什么矩阵的高是三个元素中的最大值,以[2,1,5,6,2,3]为例,其实对于5、6,遍历到2的时候,其实算了两次才到10;先算的6,结果6;然后算的5,5*2才是最终结果10,矩阵的高其实是栈中最高的那个元素的大小
else {while (!st.empty() && heights[i] < heights[st.top()]) { int mid = st.top();st.pop();if (!st.empty()) {int left = st.top();int right = i;int w = right - left - 1;int h = heights[mid];res = max(res, w * h);}}st.push(i);
}
修改后的完整代码如下:
class Solution {
public:int largestRectangleArea(vector<int>& heights) {//递减的单调栈,等发现当前元素大于栈顶元素,说明找到右边第一个更大的了heights.insert(heights.begin(), 0); // 数组头部加入元素0heights.push_back(0); // 数组尾部加入元素0int res = heights[0];stack<int> st; st.push(0);for(int i = 1; i < heights.size(); i++) {if(heights[i] >= heights[st.top()]) {st.push(i);}else {while (!st.empty() && heights[i] < heights[st.top()]) { int mid = st.top();st.pop();if (!st.empty()) {int left = st.top();int right = i;int w = right - left - 1;int h = heights[mid];res = max(res, w * h);}}st.push(i);}}return res;}
};
代码随想录详细思路:
本地单调栈的解法和接雨水的题目是遥相呼应的
为什么这么说呢,leetcode 42:接雨水 是找每个柱子左右两边第一个大于该柱子高度的柱子,而本题是找每个柱子左右两边第一个小于该柱子的柱子
这里就涉及到了单调栈很重要的性质,就是单调栈里的顺序,是从小到大还是从大到小
在 leetcode 42:接雨水 中我讲解了接雨水的单调栈从栈头(元素从栈头弹出)到栈底的顺序应该是从小到大的顺序
那么因为本题是要找每个柱子左右两边第一个小于该柱子的柱子,所以从栈头(元素从栈头弹出)到栈底的顺序应该是从大到小的顺序
举一个例子,如图:
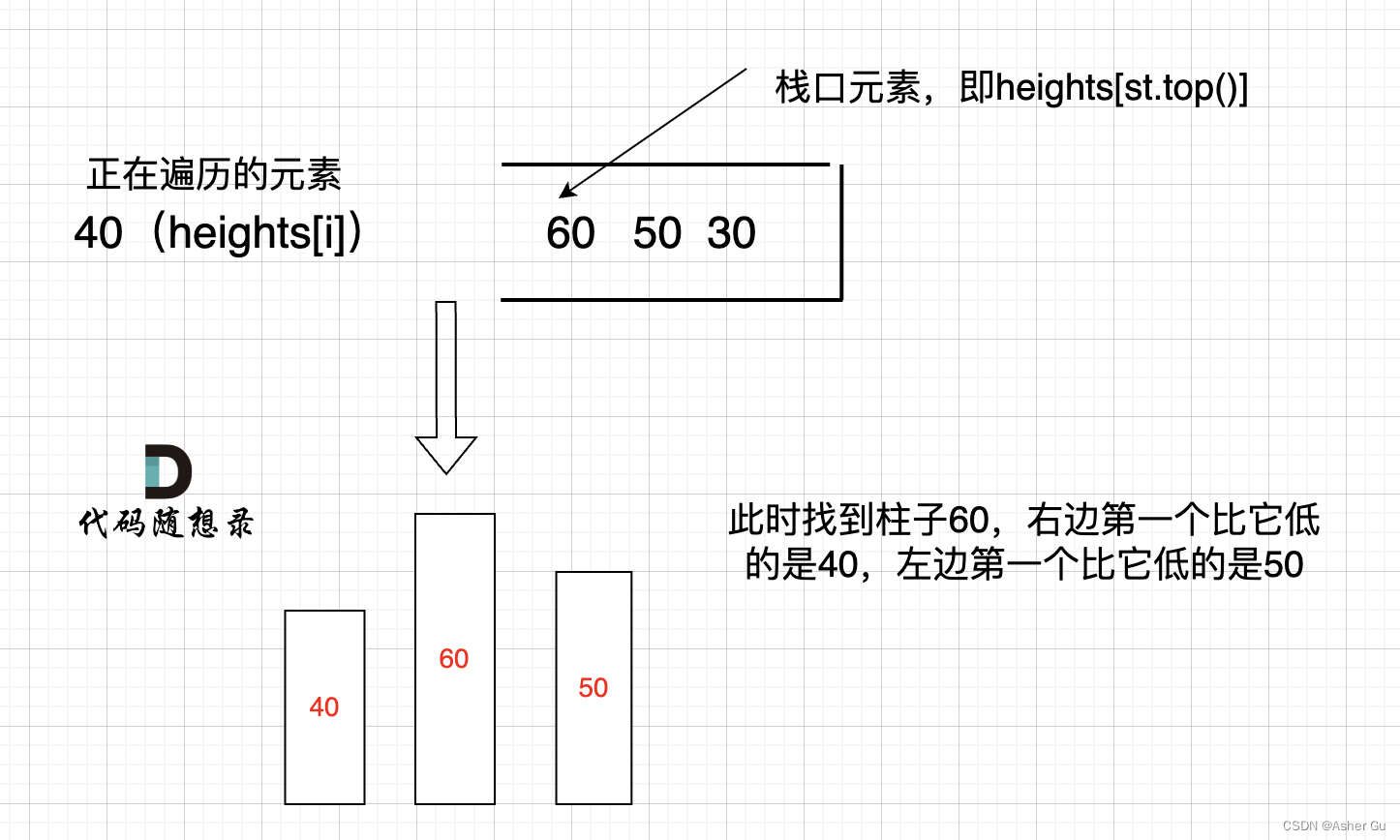
只有栈里从大到小的顺序,才能保证栈顶元素找到左右两边第一个小于栈顶元素的柱子
所以本题单调栈的顺序正好与接雨水反过来
此时大家应该可以发现其实就是栈顶和栈顶的下一个元素以及要入栈的 一共三个元素组成了我们要求最大面积的高度和宽度
除了栈内元素顺序和接雨水不同,剩下的逻辑就都差不多了
主要就是分析清楚如下三种情况:
情况一:当前遍历的元素heights[i]大于栈顶元素heights[st.top()]的情况
情况二:当前遍历的元素heights[i]等于栈顶元素heights[st.top()]的情况
情况三:当前遍历的元素heights[i]小于栈顶元素heights[st.top()]的情况
代码随想录C++代码如下:
class Solution {
public:int largestRectangleArea(vector<int>& heights) {int result = 0;stack<int> st;heights.insert(heights.begin(), 0); // 数组头部加入元素0heights.push_back(0); // 数组尾部加入元素0st.push(0);// 第一个元素已经入栈,从下标1开始for (int i = 1; i < heights.size(); i++) {if (heights[i] > heights[st.top()]) { // 情况一st.push(i);} else if (heights[i] == heights[st.top()]) { // 情况二st.pop(); // 这个可以加,可以不加,效果一样,思路不同st.push(i);} else { // 情况三while (!st.empty() && heights[i] < heights[st.top()]) { // 注意是whileint mid = st.top();st.pop();if (!st.empty()) {int left = st.top();int right = i;int w = right - left - 1;int h = heights[mid];result = max(result, w * h);}}st.push(i);}}return result;}
};
首先来说末尾为什么要加元素0?
如果数组本身就是升序的,例如[2,4,6,8],那么入栈之后 都是单调递减,一直都没有走 情况三 计算结果的那一步,所以最后输出的就是0了。 如图:
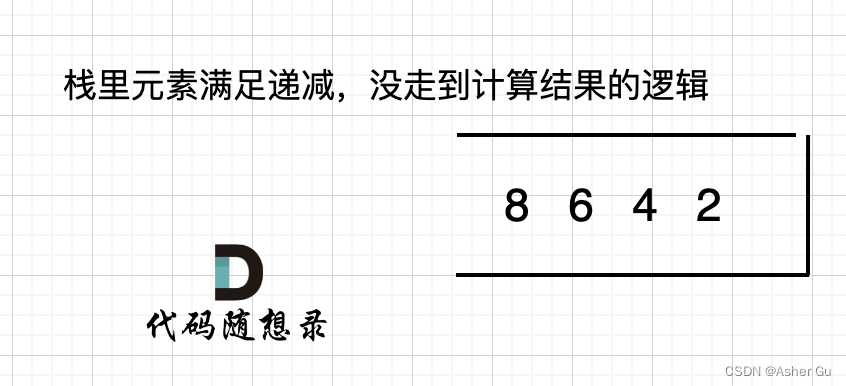
那么结尾加一个0,就会让栈里的所有元素,走到情况三的逻辑
开头为什么要加元素0?
如果数组本身是降序的,例如 [8,6,4,2],在 8 入栈后,6 开始与8 进行比较,此时我们得到 mid(8),rigt(6),但是得不到 left
(mid、left,right 都是对应代码随想录实现代码里的逻辑)
因为 将 8 弹出之后,栈里没有元素了,那么为了避免空栈取值,直接跳过了计算结果的逻辑
之后又将6 加入栈(此时8已经弹出了),然后 就是 4 与 栈口元素 8 进行比较,周而复始,那么计算的最后结果result就是0。 如图所示:
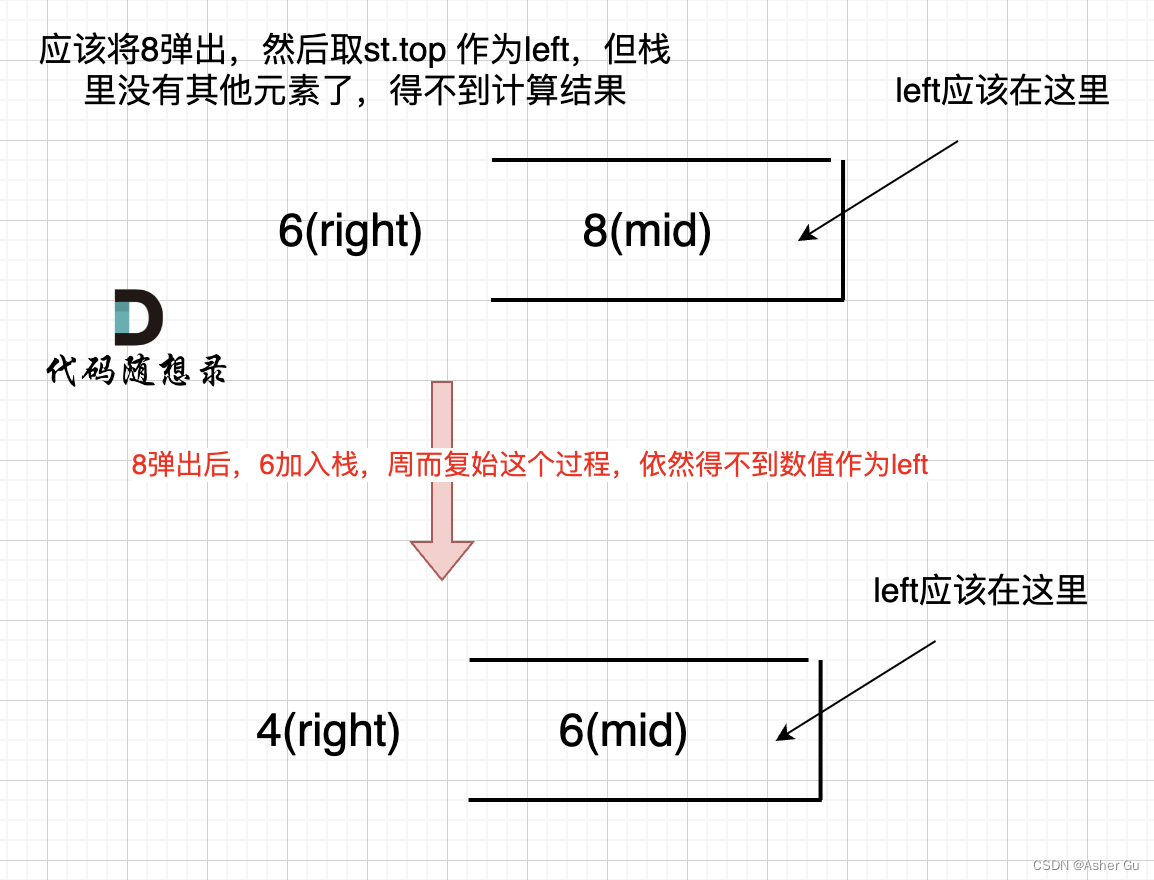
所以我们需要在 height数组前后各加一个元素0
2、代码随想录主要题目结束
曲曲折折写到这里,人间忽晚,山河已秋
其实也就三个月不到







![2023年中国聚氨酯树脂涂料需求量、市场规模及行业趋势分析[图]](https://img-blog.csdnimg.cn/img_convert/23b79af19c919003a219a25dd00619c9.png)