Git 利器 - 分支
- 1.分支 Branch
- 2.分支指令 🔥
- 3.分支的切换 checkout
- 4.合并 merge & 冲突
- 4.1 🔸 快速合并(Fast forward)
- 4.2 🔸 普通合并
- 4.3 处理冲突 <<<<<<< HEAD
- 5.变基 rebase
分支是从主线分离出去的 “副本”,分支就像是平行宇宙,可独立发展,独立编辑、提交,也可以和其他分支合并。分支是 Git 的核心必杀利器之一,分支创建、切换、删除都非常快,它非常的轻量。所以,早建分支!多用分支!

1.分支 Branch
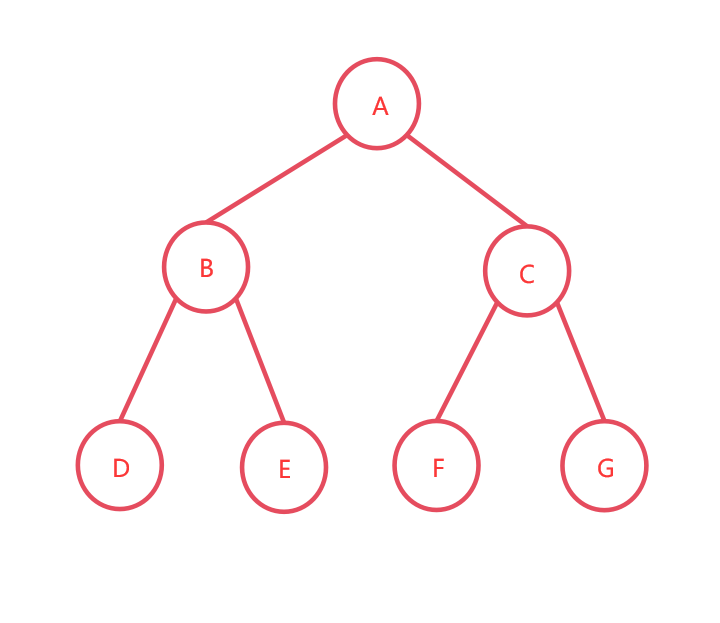
比如有一个项目团队,准备 10 月份发布新版本,要新开发一堆黑科技功能,占领市场。你和小伙伴 “小美” 一起负责开发一个新功能 A,开发周期 2 周,在这两周你们的代码不能影响其他人,不影响主分支。这个时候就可以为这个新功能创建一个分支,你们两在这个分支上干活,2 周后代码开发完了、测试通过,就可以合并进要发版的开发分支了。安全、高效,不影响其他人工作,完美!

在实际项目中,一般会建几个主线分支。
- 🔸 master:作为主分支,存放稳定的代码,就是开发后测试通过的代码,不允许随便修改和合并。
- 🔸 开发分支:用于团队日常开发用,比如团队计划 10 月份开发 10 个功能并发版,则在此分支上进行,不影响主分支的稳定。
- 🔸 功能 A 分支:开发人员根据自己的需要,可以创建一些临时分支用于特定功能的开发,开发完毕后再合并到开发分支,并删除该分支。
分支就是指向某一个提交记录的 “指针” 引用,因此创建分支是非常快的,不管仓库多大。当我们运行 git branch dev 创建了一个名字为 dev 的分支,Git 实际上是在 .git\refs\heads 下创建一个 dev 的引用文件(没有扩展名)。
$ git branch dev
$ cat .git/refs/heads/dev
ca88989e7c286fb4ba56785c2cd8727ea1a07b97
2.分支指令 🔥
| | |
|---|---|
git branch | 列出所有本地分支,加参数 -v 显示详细列表,下同 |
git branch -r | 列出所有远程分支 |
git branch -a | 列出所有本地分支和远程分支,用不同颜色区分 |
git branch [branch-name] | 新建一个分支,但依然停留在当前分支 |
git branch -d dev | 删除 dev 分支,-D(大写)强制删除 |
git checkout -b dev | 从当前分支创建并切换到 dev 分支 |
git checkout -b feature1 dev | 从本地 dev 分支代码创建一个 feature1 分支,并切换到新分支 |
git branch [branch] [commit] | 新建一个分支,指向指定 commit id |
git branch --track [branch] [remote-branch] | 新建一个分支,与指定的远程分支建立关联 |
git checkout -b hotfix remote hotfix | 从远端 remote 的 hotfix 分支创建本地 hotfix 分支 |
git branch --set-upstream [branch] [remote-branch] | 在现有分支与指定的远程分支之间建立跟踪关联:git branch --set-upstream hotfix remote/hotfix |
git checkout [branch-name] | 切换到指定分支,并更新工作区 |
git checkout . | 撤销工作区的(未暂存)修改,把暂存区恢复到工作区 |
git checkout HEAD . | 撤销工作区、暂存区的修改,用 HEAD 指向的当前分支最新版本替换 |
git merge [branch] | 合并指定分支到当前分支 |
git merge --no-ff dev | 合并 dev 分支到当前分支,参数 --no-ff 禁用快速合并模式 |
git push origin --delete [branch-name] | 删除远程分支 |
git rebase master | 将当前分支变基合并到 master 分支 |
✅switch:新的分支切换指令 | 切换功能和 checkout 一样,switch 只单纯的用于切换 |
git switch master | 切换到已有的 master 分支 |
git switch -c dev | 创建并切换到新的 dev 分支 |
📢 关于
checkout指令:checkout是 Git 的底层指令,比较常用,也比较危险,它会重写工作区。支持的功能比较多,能撤销修改,能切换分支,这也导致了这个指令比较复杂。在 Git 2.23 版本以后,增加了git switch、git reset指令。
git switch:专门用来实现分支切换。git reset:专门用来实现本地修改的撤销,更多可参考后续 “reset” 内容。
$ git branchdev
* main
# 列出了当前的所有分支,星号“*”开头的“main”为当前活动分支。
3.分支的切换 checkout
代码仓库可以有多个分支,master 为默认的主分支,但只有一个分支在工作状态。所以要操作不同分支,需要切换到该分支,HEAD 就是指向当前正在活动的分支。

# 切换到dev分支,HEAD指向了dev
# 此处 switch 作用同 checkout,switch只用于切换,不像checkout功能很多
$ git switch dev
Switched to branch 'dev'
$ cat .git/HEAD
ref: refs/heads/dev
使用 git checkout dev 切换分支时,干了两件事:
- ①
HEAD指向dev:修改HEAD的 “指针” 引用,指向dev分支。 - ② 还原工作空间:把
dev分支内容还原到工作空间。
此时的活动分支就是 dev 了,后续的提交就会更新到 dev 分支了。
❓ 切换时还没提交的代码怎么办?
- 如果修改(包括未暂存、已暂存)和待切换的分支没有冲突,则切换成功,且未提交修改会一起带过去,所以要注意!
- 如果有冲突,则会报错,提示先提交或隐藏,关于隐藏可查看后续章节内容 “stash”。
4.合并 merge & 冲突
把两个分支的修改内容合并到一起,常用的合并指令 git merge [branch],将分支 [branch] 合并到当前分支。根据要合并的内容的不同,具体合并过程就会有多种情况。

4.1 🔸 快速合并(Fast forward)
如下图,master 分支没有任何提交,git merge dev 合并分支 dev 到 master,此时合并速度就非常快,直接移动 master 的 “指针” 引用到 dev 即可。这就是快速合并(Fast forward),不会产生新的提交。

合并 dev 到 master,注意要先切换到 master 分支,然后执行 git merge dev,把 dev 合并到当前分支。
📢 强制不用快速合并:
git merge --no-ff -m “merge with no-ff” dev,参数--no-ff不启用快速合并,会产生一个新的合并提交记录。
4.2 🔸 普通合并
如果 master 有变更,存在分支交叉,则会把两边的变更合并成一个提交。
- 如果两边变更的文件不同,没有什么冲突,就自动合并了。
- 如果有修改同一个文件,则会存在冲突,到底该采用哪边的,程序无法判断,就换产生冲突。冲突内容需要人工修改后再重新提交,才能完成最终的合并。

上图中,创建 dev 分支后,两个分支都有修改提交,因此两个分支就不在一条顺序线上了,此时合并 dev 到 master 就得把他们的修改进行合并操作了。
v5、v7共同祖先是v4,从这里开始分叉。- Git 会用两个分支的末端
v6和v8以及它们的共同祖先v4进行三方合并计算。合并之后会生成一个新(和并)提交v9。 - 合并提交
v9就有两个祖先v6、v8。
4.3 处理冲突 <<<<<<< HEAD
在有冲突的文件中,<<<<<<< HEAD 开头的内容就表示是有冲突的部分,需要人工处理,可以借助一些第三方的对比工具。人工处理完毕后,完成合并提交,才最终完成此次合并。======= 分割线上方是当前分支的内容,下方是被合并分支的变更内容。

5.变基 rebase
把两个分支的修改内容合并到一起的办法有两种:merge 和 rebase,作用都是一样的,区别是 rebase 的提交历史更简洁,干掉了分叉,merge 的提交历史更完整。

- 在
dev上执行git rebase master变基,将dev分支上分叉的v7、v8生成补丁,然后在master分支上应用补丁,产生新的v7’、v8’新的提交。 - 然后回到
master分支,完成合并git merge dev,此时的合并就是快速合并了。 - 最终的提交记录就没有分叉了。
$ git rebase master
$ git checkout master
$ git merge dev