题目描述:
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
void push(int x)将元素 x 压入栈顶。int pop()移除并返回栈顶元素。int top()返回栈顶元素。boolean empty()如果栈是空的,返回true;否则,返回false。
注意:
- 你只能使用队列的基本操作 —— 也就是
push to back、peek/pop from front、size和is empty这些操作。 - 你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
功能实现思路:
在实现这个题目之前得先完成队列的基本操作,可以参考文章:http://t.csdnimg.cn/3v2IZ
1. 出栈
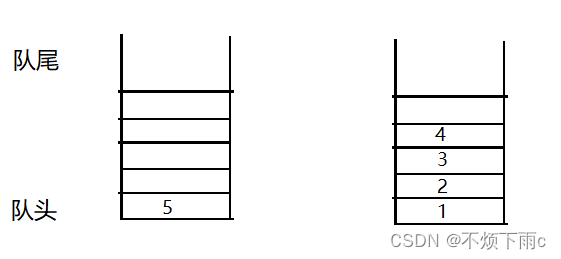
现在我们有两个队列,假设在第一个队列里依次入了1 2 3 4 5,另一个队列为空队列
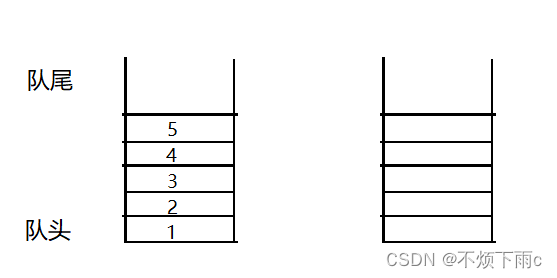
现在要出栈的话,应该把5出去,但是数据目前在队列里,出数据只能从队头出,所以可以把1 2 3 4依次出队列,并入到第二个队列中,此时就可以把5出去了,此时又是一个队列为空,另一个存着剩余的数据,再出栈的话,还按照这个方法即可
int myStackPop(MyStack* obj) {//由于不知道哪个队列为空队列,可以采用假设法Queue* empty = &obj->queue1;Queue* nonempty=&obj->queue2;if(!QueueEmpty(&obj->queue1)){empty=&obj->queue2;nonempty=&obj->queue1;}while(QueueSize(nonempty)>1){QueuePush(empty,QueueFront(nonempty));QueuePop(nonempty);}int top=QueueFront(nonempty);QueuePop(nonempty);return top;
}总结:
出栈操作相当于非空队列的队尾元素出队,此时需要把非空队列除最后一个元素之外的其他元素入队到空队列,然后出队最后一个队尾元素
2.入栈
入栈操作相当于在非空队列进行入队操作
void myStackPush(MyStack* obj, int x) {if(!QueueEmpty(&obj->queue1)){QueuePush(&obj->queue1,x);}else{QueuePush(&obj->queue2,x);}
}3.判空
只要两个队列都没有元素就表示栈空
bool myStackEmpty(MyStack* obj) {return QueueEmpty(&obj->queue1)&&QueueEmpty(&obj->queue2);
}4.返回栈顶元素
即返回非空队列队尾元素
int myStackTop(MyStack* obj) {if(!QueueEmpty(&obj->queue1)){return QueueTail(&obj->queue1);}else{return QueueTail(&obj->queue2);}
}typedef int QDataType;
typedef struct QueueNode {QDataType x;struct QueueNode* next;
}Node;typedef struct Queue
{Node* head;Node* tail;int size;
}Queue;void QueueInit(Queue* ps)
{assert(ps);ps->head = ps->tail = NULL;ps->size = 0;
}void QueuePush(Queue* ps, QDataType x)
{assert(ps);//创建新节点Node* newnode = (Node*)malloc(sizeof(Node));if (newnode == NULL){perror("malloc");return;}newnode->next = NULL;newnode->x = x;//尾插if (ps->tail == NULL){ps->head = ps->tail = newnode;}else{ps->tail->next = newnode;ps->tail = ps->tail->next;}ps->size++;
}void QueuePop(Queue* ps)
{assert(ps);assert(ps->head);if (ps->head->next == NULL){ps->head = ps->tail = NULL;}else{Node* next = ps->head->next;free(ps->head);ps->head = next;}ps->size--;
}bool QueueEmpty(Queue* ps)
{assert(ps);return ps->tail == NULL;
}QDataType QueueFront(Queue* ps)
{assert(ps);assert(ps->head);return ps->head->x;
}QDataType QueueTail(Queue* ps)
{assert(ps);assert(ps->tail);return ps->tail->x;
}int QueueSize(Queue* ps)
{assert(ps);return ps->size;
}void QueueDestory(Queue* ps)
{assert(ps);Node* cur = ps->head;while (cur){Node* next = cur->next;free(cur);cur = next;}ps->head=ps->tail = NULL;ps->size=0;
}typedef struct {Queue queue1;Queue queue2;
} MyStack;MyStack* myStackCreate() {MyStack* mystack=(MyStack*)malloc(sizeof(MyStack));QueueInit(&mystack->queue1);QueueInit(&mystack->queue2);return mystack;
}void myStackPush(MyStack* obj, int x) {if(!QueueEmpty(&obj->queue1)){QueuePush(&obj->queue1,x);}else{QueuePush(&obj->queue2,x);}
}int myStackPop(MyStack* obj) {Queue* empty = &obj->queue1;Queue* nonempty=&obj->queue2;if(!QueueEmpty(&obj->queue1)){empty=&obj->queue2;nonempty=&obj->queue1;}while(QueueSize(nonempty)>1){QueuePush(empty,QueueFront(nonempty));QueuePop(nonempty);}int top=QueueFront(nonempty);QueuePop(nonempty);return top;
}int myStackTop(MyStack* obj) {if(!QueueEmpty(&obj->queue1)){return QueueTail(&obj->queue1);}else{return QueueTail(&obj->queue2);}
}bool myStackEmpty(MyStack* obj) {return QueueEmpty(&obj->queue1)&&QueueEmpty(&obj->queue2);
}void myStackFree(MyStack* obj) {QueueDestory(&obj->queue1);QueueDestory(&obj->queue2);free(obj);
}