1 pdist
计算n维空间中观测点之间的成对距离。
scipy.spatial.distance.pdist(X, metric='euclidean', *, out=None, **kwargs)1.1 主要参数
| X | 一个m行n列的数组,表示n维空间中的m个原始观测点 |
| metric | 使用的距离度量 |
| out | 输出数组。如果非空,压缩的距离矩阵Y将存储在此数组中 |
1.2 举例
import numpy as np
from scipy.spatial.distance import pdistx = np.array([[2, 0, 2], [2, 2, 3], [-2, 4, 5], [0, 1, 9], [2, 2, 4]])
#5个元素,每个元素3维pdist(x)
#array([2.23606798, 6.40312424, 7.34846923, 2.82842712, 4.89897949,6.40312424, 1. , 5.38516481, 4.58257569, 5.47722558])
'''
10个元素,分别表示:第1个点和第2个点之间的距离
第1个点和第3个点之间的距离
第1个点和第4个点之间的距离
第1个点和第5个点之间的距离
第2个点和第3个点之间的距离
第2个点和第4个点之间的距离
第2个点和第5个点之间的距离
第3个点和第4个点之间的距离
第3个点和第5个点之间的距离
第4个点和第5个点之间的距离
'''2 cdist
计算两个输入集合中每对元素之间的距离
scipy.spatial.distance.cdist(XA, XB, metric='euclidean', *, out=None, **kwargs)2.1 主要参数
| XA | mA*n的矩阵,表示mA个元素,每个元素n维特征 |
| XB | mBn的矩阵,表示mB个元素,每个元素n维特征 |
| metric | 使用的距离度量 |
| out | 输出数组(mA*mB)。如果非空,压缩的距离矩阵Y将存储在此数组中 |
2.2 举例
import numpy as np
from scipy.spatial.distance import cdistx = np.array([[2, 0, 2], [2, 2, 3], [-2, 4, 5], [0, 1, 9], [2, 2, 4]])cdist(x,x)
'''
array([[0. , 2.23606798, 6.40312424, 7.34846923, 2.82842712],[2.23606798, 0. , 4.89897949, 6.40312424, 1. ],[6.40312424, 4.89897949, 0. , 5.38516481, 4.58257569],[7.34846923, 6.40312424, 5.38516481, 0. , 5.47722558],[2.82842712, 1. , 4.58257569, 5.47722558, 0. ]])
'''y=[[1,2,3]]
cdist(x,y)
'''
array([[2.44948974],[1. ],[4.12310563],[6.164414 ],[1.41421356]])
'''cdist(y,x)
'''
array([[2.44948974, 1. , 4.12310563, 6.164414 , 1.41421356]])
'''3 squareform
将距离向量的向量形式转换为方阵形式的距离矩阵,反之亦然。
scipy.spatial.distance.squareform(X, force='no', checks=True)
3.1 举例
import numpy as np
from scipy.spatial.distance import *x = np.array([[2, 0, 2], [2, 2, 3], [-2, 4, 5], [0, 1, 9], [2, 2, 4]])dist_vec=pdist(x)
dist_vec
'''
array([2.23606798, 6.40312424, 7.34846923, 2.82842712, 4.89897949,6.40312424, 1. , 5.38516481, 4.58257569, 5.47722558])
'''dist_mat=squareform(dist_vec)
dist_mat
'''
array([[0. , 2.23606798, 6.40312424, 7.34846923, 2.82842712],[2.23606798, 0. , 4.89897949, 6.40312424, 1. ],[6.40312424, 4.89897949, 0. , 5.38516481, 4.58257569],[7.34846923, 6.40312424, 5.38516481, 0. , 5.47722558],[2.82842712, 1. , 4.58257569, 5.47722558, 0. ]])
'''squareform(dist_mat)
'''
array([2.23606798, 6.40312424, 7.34846923, 2.82842712, 4.89897949,6.40312424, 1. , 5.38516481, 4.58257569, 5.47722558])
'''4 directed_hausdorff
- 计算两个二维数组之间的定向豪斯多夫距离
- 通常用于衡量两个点集合的相似性
scipy.spatial.distance.directed_hausdorff(u, v, seed=0)数学笔记/scipy 笔记:豪斯多夫距离(Hausdorff )_python 豪斯多夫距离-CSDN博客
4.1 主要参数
| u | (M,N)大小的数组 M 表示点的数量,N 表示每个点的维度 |
| v | (O,N)大小的数组 O 表示点的数量,N 表示每个点的维度 |
4.2 返回内容
| d | u 和 v 之间的定向豪斯多夫距离 |
| index_1 | 在数组u中贡献豪斯多夫对的点的索引 |
| index_2 | 在数组v中贡献豪斯多夫对的点的索引 |
4.3 举例
import numpy as np
from scipy.spatial.distance import *u = np.array([(1.0, 0.0),(0.0, 1.0),(-1.0, 0.0),(0.0, -1.0)])
v = np.array([(2.0, 0.0),(0.0, 2.0),(-2.0, 0.0),(0.0, -4.0)])directed_hausdorff(u,v)
#(2.23606797749979, 3, 0)5 is_valid_dm
判断输入数组是否为有效的距离矩阵
scipy.spatial.distance.is_valid_dm(D, tol=0.0, throw=False, name='D', warning=False)5.1 主要参数
| D | 用于测试有效性的候选对象 |
| tol | 距离矩阵应该是对称的。tol是条目ij和ji之间的最大差异,以便将距离度量视为对称 |
5.2 举例
import numpy as np
from scipy.spatial.distance import *d = np.array([[0.0, 1.1, 1.2, 1.3],[1.1, 0.0, 1.0, 1.4],[1.2, 1.0, 0.0, 1.5],[1.3, 1.4, 1.5, 0.0]])
is_valid_dm(d)
#Trueis_valid_dm([[0, 2, 2], [2, 0, 2]])
#形状不对is_valid_dm([[0, 1, 1], [1, 2, 3], [1, 3, 0]])
#对角线不为0is_valid_dm([[0, 1, 3], [2, 0, 1], [3, 1, 0]])
#不对称6 is_valid_y
scipy.spatial.distance.is_valid_y(y, warning=False, throw=False, name=None)判断输入数组是否为有效的压缩距离矩阵。
压缩距离矩阵必须是1维的numpy数组。它们的长度必须是一些正整数n的二项系数
6.1 主要参数
| y | 压缩距离矩阵 |
6.2 举例
import numpy as np
from scipy.spatial.distance import *is_valid_y([1.0, 1.2, 1.0, 0.5, 1.3, 0.9])
#True
#长度为6,合理长度,所以返回Trueis_valid_y([1.0, 1.2, 1.0, 0.5, 1.3, 0.9,1.5])
#False
#长度为7,不合理长度,所以返回False7 两个数字向量之间的距离
7.1 braycurtis
计算两个一维数组之间的布雷-柯蒂斯距离
scipy.spatial.distance.braycurtis(u, v, w=None)

7.1.1 主要参数
| u | (N,) 输入数组 |
| v | (N,) 输入数组 |
| w | (N,) u和v中每个值的权重 |
7.1.2 举例
基本上后面都是一样的,就不举例了
import numpy as np
from scipy.spatial.distance import *braycurtis([1,1,0],[0,1,0])#0.3333333333333333
7.2 canberra
scipy.spatial.distance.canberra(u, v, w=None)
7.3 chebyshev
scipy.spatial.distance.chebyshev(u, v, w=None)

7.4 cityblock
曼哈顿距离
scipy.spatial.distance.cityblock(u, v, w=None)
7.5 correlation
scipy.spatial.distance.correlation(u, v, w=None, centered=True)
7.6 cosine
scipy.spatial.distance.cosine(u, v, w=None)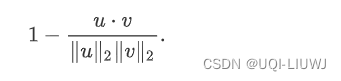
7.7 euclidean
scipy.spatial.distance.euclidean(u, v, w=None)7.8 jensenshannon
scipy.spatial.distance.jensenshannon(p, q, base=None, *, axis=0, keepdims=False)两个概率向量p,q之间的JS距离
如果p和q的总和不为1.0,该程序将对其进行归一化


7.8.1 主要参数
| p | 左侧概率向量 |
| q | 右侧概率向量 |
| base | 用于计算输出的对数底数 |
| axis | 沿着哪个轴计算JS距离 |
7.8.2 举例
import numpy as np
from scipy.spatial.distance import *jensenshannon([1.0, 0.0, 0.0], [0.0, 1.0, 0.0])
#0.8325546111576977jensenshannon([1.0, 0.0, 0.0], [0.0, 1.0, 0.0],2)
#1.0a = np.array([[1, 2, 3, 4],[5, 6, 7, 8],[9, 10, 11, 12]])
b = np.array([[13, 14, 15, 16],[17, 18, 19, 20],[21, 22, 23, 24]])
jensenshannon(a, b, axis=0)
#array([0.19542878, 0.14476971, 0.11383771, 0.09276358])jensenshannon(a, b, axis=1)
#array([0.14023394, 0.03991063, 0.02018153])7.9 mahalanobis
马氏距离
scipy.spatial.distance.mahalanobis(u, v, VI)

7.9.1 主要参数
| u | 输入向量 |
| v | 输入向量 |
| VI | 协方差矩阵的逆,也即上面公式中的 |
7.9.2 举例
import numpy as np
from scipy.spatial.distance import *iv = [[1, 0.5, 0.5], [0.5, 1, 0.5], [0.5, 0.5, 1]]mahalanobis([1, 0, 0], [0, 1, 0], iv)
#1.07.10 minkowski
闵可夫斯基距离
scipy.spatial.distance.minkowski(u, v, p=2, w=None)
7.11 seuclidean
标准欧氏距离
scipy.spatial.distance.seuclidean(u, v, V)

V[i]是针对点集中所有第i个分量计算得到的方差
7.12 sqeuclidean
平方欧氏距离
scipy.spatial.distance.sqeuclidean(u, v, w=None)
8 两个布尔向量距离
8.1 dice
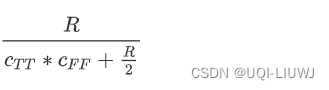
scipy.spatial.distance.dice(u, v, w=None)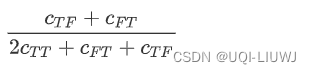
CTF表示u是T,v是F,其他类似
8.2 hamming
scipy.spatial.distance.hamming(u, v, w=None)
8.3 jaccard
scipy.spatial.distance.jaccard(u, v, w=None)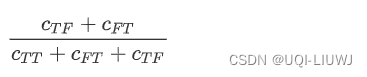
8.4 kulczynski1
scipy.spatial.distance.kulczynski1(u, v, *, w=None)
8.5 rogerstanimoto
scipy.spatial.distance.rogerstanimoto(u, v, w=None)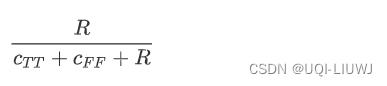

8.6 russellrao

8.7 sokalmichener
scipy.spatial.distance.sokalmichener(u, v, w=None)
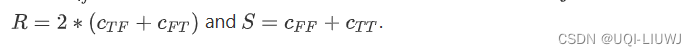
8.8 sokalsneath
scipy.spatial.distance.sokalsneath(u, v, w=None)

8.9 yule
scipy.spatial.distance.yule(u, v, w=None)