许多微控制器没有浮点单元,但确实有一个(合理)快速整数除法单元。在这些情况下,使用有理值来近似浮点常数可能是值得的.
例如,355/113 = 3.1415929203539823008849557522124 是 π = 3.14159265358979323846 一个很好的近似值.
最佳有理近似 p/q到实数 x 最多有分母 M 是一个有理数 p/q(最低限度) 跟 q≤M这样, 对于任何整数 a和 b ≤M , a 和 b 互素 , p/q 至少与 a/b 一样接近 x : |x – p/q|≤|x – a/b|.
编写程序来计算最佳有理近似 到一个实数 x , 最多有分母 M.
(题目大意) 在给定范围内找到两个数,使其相除后的商最接近给定的小数
输入
第一行输入包含一个整数 P (1≤P≤1000),即后面的数据集数。每个数据集都应以相同且独立的方式进行处理。
每个数据集都由一行输入组成。它包含数据集编号 K,后跟最大分母值 M (15≤M≤100000),后跟浮点值 x(0≤x < 1)。
输出
对于每个数据集,都有一行输出。单行输出线由数据集编号 K 组成,后跟一个空格,后跟 x 的最佳有理近似分子 p,后跟正斜杠 (/),后跟 x 的最佳有理近似分母 q。
Input
3
1 100000 0.141592653589793238
2 255 0.141592653589793238
3 15 0.141592653589793238
Output
1 14093/99532
2 16/113
3 1/7
解析:
Stern–Brocot 树
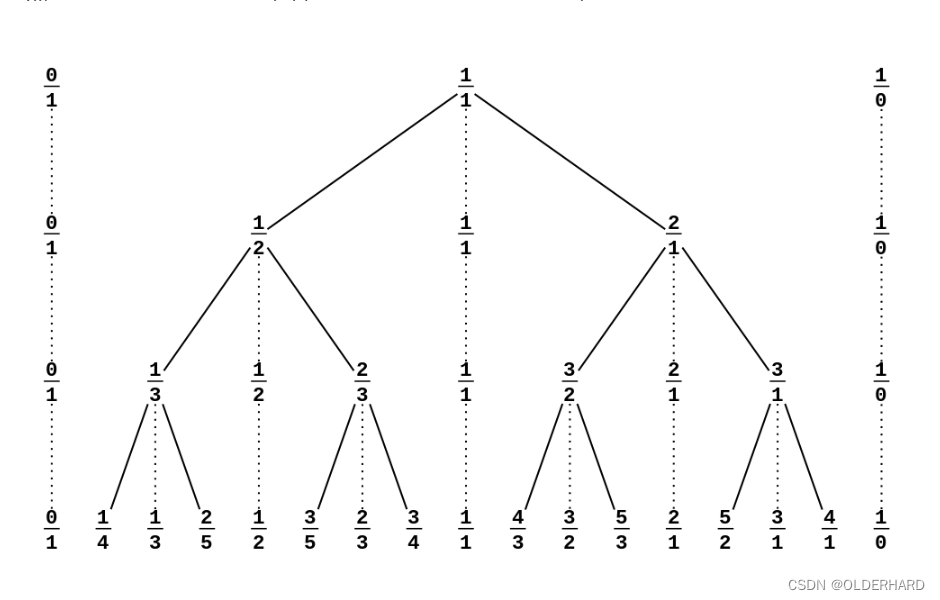
从第1行到第n行,每行相邻两数a/b和c/d,产生中间数(a+c)/(b+d),置于下一行中,
其中真分数 (左边),叫法里数列(Farey 数列)
法里数列 在每层中单调递增(易证) 并且具有最简性(也就是分子和分母互质), 这样就可以通过二分的方法来找到最佳有理近似p/q ——另类的二分
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
typedef pair<int,int> PII;
const int N=2e6+10;
double p;
int t,k,m;
signed main()
{ios;cin>>t;while(t--){cin>>k>>m>>p;int a=0,b=1,c=1,d=1;int x,y;while (1){x=a+c;y=b+d;if (y>m) break; if (1.0*x/y<=p) {a=x;b=y;}else{c=x;d=y;}}cout<<k<<" ";if (fabs(1.0*a/b-p)>fabs(1.0*c/d-p)){cout<<c<<"/"<<d<<endl;}else cout<<a<<"/"<<b<<endl;}return 0;
}