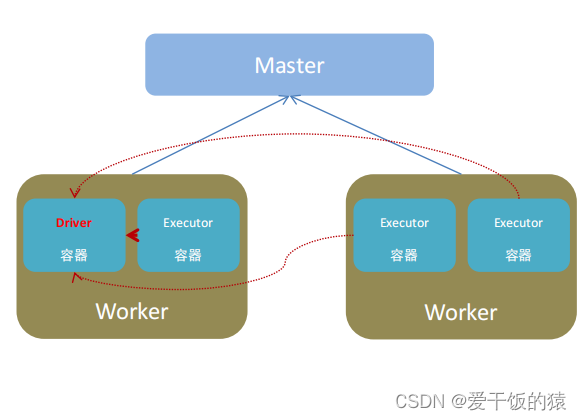
ABY3中采用replicated secret sharing（复制秘密分享）机制，即2-out-of-3秘密分享，三个参与方的每一方都拥有share中的两份。下面来看一下这样做有什么好处。

2-out-of-3秘密分享

有$x,y$两个操作数，先进行秘密分享：

• $P_1$拥有$(x_1,x_2),(y_1,y_2)$
• $P_2$拥有$(x_2,x_3),(y_2,y_3)$
• $P_3$拥有$(x_3,x_1),(y_3,y_1)$

常见的计算

1 加法

$⟨x+y⟩=(x_1+y_1,x_2+y_2,x_3+y_3)$

2 加常数

$⟨x⟩+c=(x_1+c,x_2,x_3)$，注意只需要加一次$c$

3 数乘

$⟨cx⟩=(c{x}_1,c{x}_2,c{x}_3)$

4 乘法

$$\begin{gathered} ⟨xy⟩=(x_1+x_2+x_3)(y_1+y_2+y_3) \\ =(x_1{y}_1+x_1{y}_2+x_1{y}_3) \\ +(x_2{y}_1+x_2{y}_2+x_2{y}_3) \\ +(x_3{y}_1+x_3{y}_2+x_3{y}_3) \\ 调整一下顺序 \\ =(x_1{y}_1+x_1{y}_2+x_2{y}_1)+{\alpha }_1[P_1\to z_1] \\ +(x_3{y}_2+x_2{y}_2+x_2{y}_3)+{\alpha }_2[P_2\to z_2] \\ +(x_3{y}_1+x_1{y}_3+x_3{y}_3)+{\alpha }_3[P_3\to z_3] \end{gathered}$$
暂不管$\alpha$，可以看到，三个参与方可以分别在本地计算出$z_1,z_2,z_3$，也就是交叉项的结果。
然而，我们要求各方都持有三份share中的两份，所以需要re-sharing操作，也就是$P_i$将$z_i$发给$P_{i-1}$。
现在来看$\alpha$的作用，$\alpha$用于随机化$z$，我们需要让$\alpha$满足：${\alpha }_1+{\alpha }_2+{\alpha }_3=0$。每一方都完全知道这三个值中的一个，这样的三元组$({\alpha }_1,{\alpha }_2,{\alpha }_3)$被称为zero-sharing（零共享），在one-time setup后的计算无需任何交互。
那么如何生成三元组？基于伪随机函数（PRF）生成，这部分本文不展开。

由此可见，3PC和2PC都在本地计算加法，他们最大的不同就是乘法：在2PC乘法中，交叉项需要借助OT或HE计算，带来巨大的通信或计算开销；而基于复制秘密分享的3PC乘法完全在本地计算交叉项，无需通信，在re-sharing时需要少量的通信。

5 截断

方法1：${\Pi }_{Trunc1}$
核心想法是在一方不参与的情况下，运行两方协议。
令各方有$⟨x^{\prime }⟩=⟨y⟩⟨z⟩$的2-out-of-3的share（上面乘法后的结果），现在的目的是计算截断$⟨x⟩=⟨x^{\prime }⟩/2^d$。
定义$P_1,P_2$之间的2-out-of-2 share为$(x_1^{\prime },x_2^{\prime }+x_3^{\prime })$，然后双方在本地截断$(x_1^{\prime }/2^d,(x_2^{\prime }+x_3^{\prime })/2^d)$，最后的结果为$⟨x⟩:=(x_1,x_2,x_3)=(x_1^{\prime }/2^d,(x_2^{\prime }+x_3^{\prime })/2^d-r,r)$，其中，$r\in {\mathbb{Z}}_2^k$是一个$P_2,P_3$知道的随机数。最后，为了让三方拥有两份share，需要再做一次re-sharing操作。
这个方法的局限性是两轮计算需要乘法和截断。

方法2：${\Pi }_{Trunc2}$