1. 理论介绍

• 将模型在训练数据上拟合的比在潜在分布中更接近的现象称为过拟合， 用于对抗过拟合的技术称为正则化。
• 训练误差和验证误差都很严重， 但它们之间差距很小。 如果模型不能降低训练误差，这可能意味着模型过于简单（即表达能力不足），无法捕获试图学习的模式。 这种现象被称为欠拟合。
• 训练误差是指模型在训练数据集上计算得到的误差。
• 泛化误差是指模型应用在同样从原始样本的分布中抽取的无限多数据样本时，模型误差的期望。我们永远不能准确地计算出泛化误差，在实际中，我们只能通过将模型应用于一个独立的测试集来估计泛化误差， 该测试集由随机选取的、未曾在训练集中出现的数据样本构成。
• 影响模型泛化的因素
  • 可调整参数的数量。当可调整参数的数量（有时称为自由度）很大时，模型往往更容易过拟合。
  • 参数采用的值。当权重的取值范围较大时，模型可能更容易过拟合。
  • 训练样本的数量。即使模型很简单，也很容易过拟合只包含一两个样本的数据集，而过拟合一个有数百万个样本的数据集则需要一个极其灵活的模型。
• 在机器学习中，我们通常在评估几个候选模型后选择最终的模型。 这个过程叫做模型选择。候选模型可能在本质上不同，也可能是不同的超参数设置下的同一类模型。
• 为了确定候选模型中的最佳模型，我们通常会使用验证集。验证集与测试集十分相似，唯一的区别是验证集是用于确定最佳模型，测试集是用于评估最终模型的性能。
• $K$折交叉验证：当训练数据稀缺时，将原始训练数据分成$K$个不重叠的子集。 然后执行$K$次模型训练和验证，每次在$(K-1)$个子集上进行训练， 并在剩余的一个子集（在该轮中没有用于训练的子集）上进行验证。 最后，通过对$K$次实验的结果取平均来估计训练和验证误差。
• 引起过拟合的因素
  • 模型复杂度
    
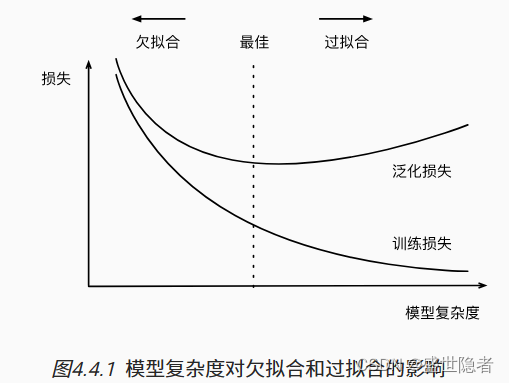
  • 数据集大小
    • 训练数据集中的样本越少，我们就越有可能（且更严重地）过拟合。
    • 给出更多的数据，拟合更复杂的模型可能是有益的； 如果没有足够的数据，简单的模型可能更有用。

2. 实例解析

2.1. 实例描述

使用以下三阶多项式来生成训练和测试数据$$y=5+1.2x-3.4\frac{x^2}{2!}+5.6\frac{x^3}{3!}+ϵ\text{ where }ϵ\sim \mathcal{N}(0,0.1^2).$$并用1阶（线性模型）、3阶、20阶多项式拟合。

2.2. 代码实现

2.2.1. 完整代码

import os
import numpy as np
import math, torch
import torch.nn as nn
from torch.utils.data import DataLoader, TensorDataset
from tensorboardX import SummaryWriter
from rich.progress import trackdef evaluate_loss(dataloader, net, criterion):"""评估模型在指定数据集上的损失"""num_examples = 0loss_sum = 0.0with torch.no_grad():for X, y in dataloader:X, y = X.cuda(), y.cuda()loss = criterion(net(X), y)num_examples += y.shape[0]loss_sum += loss.sum()return loss_sum / num_examplesdef load_dataset(*tensors):"""加载数据集"""dataset = TensorDataset(*tensors)return DataLoader(dataset, batch_size, shuffle=True)if __name__ == '__main__':# 全局参数设置num_epochs = 400batch_size = 10learning_rate = 0.01# 创建记录器def log_dir():root = "runs"if not os.path.exists(root):os.mkdir(root)order = len(os.listdir(root)) + 1return f'{root}/exp{order}'writer = SummaryWriter(log_dir())# 生成数据集max_degree = 20             # 多项式最高阶数n_train, n_test = 100, 100  # 训练集和测试集大小true_w = np.zeros(max_degree+1)true_w[0:4] = np.array([5, 1.2, -3.4, 5.6])features = np.random.normal(size=(n_train + n_test, 1))np.random.shuffle(features)poly_features = np.power(features, np.arange(max_degree+1).reshape(1, -1))for i in range(max_degree+1):poly_features[:, i] /= math.gamma(i + 1)  # gamma(n)=(n-1)!labels = np.dot(poly_features, true_w)labels += np.random.normal(scale=0.1, size=labels.shape)    # 加高斯噪声服从N(0, 0.01)poly_features, labels = [torch.as_tensor(x, dtype=torch.float32) for x in [poly_features, labels.reshape(-1, 1)]]def loop(model_degree):# 创建模型net = nn.Linear(model_degree+1, 1, bias=False).cuda()nn.init.normal_(net.weight, mean=0, std=0.01)criterion = nn.MSELoss(reduction='none')optimizer = torch.optim.SGD(net.parameters(), lr=learning_rate)# 加载数据集dataloader_train = load_dataset(poly_features[:n_train, :model_degree+1], labels[:n_train])dataloader_test = load_dataset(poly_features[n_train:, :model_degree+1], labels[n_train:])# 训练循环for epoch in track(range(num_epochs), description=f'{model_degree}-degree'):for X, y in dataloader_train:X, y = X.cuda(), y.cuda()loss = criterion(net(X), y)optimizer.zero_grad()loss.mean().backward()optimizer.step()writer.add_scalars(f"{model_degree}-degree", {"train_loss": evaluate_loss(dataloader_train, net, criterion),"test_loss": evaluate_loss(dataloader_test, net, criterion),}, epoch)print(f"{model_degree}-degree: weights =", net.weight.data.cpu().numpy())for model_degree in [1, 3, 20]:loop(model_degree)writer.close()

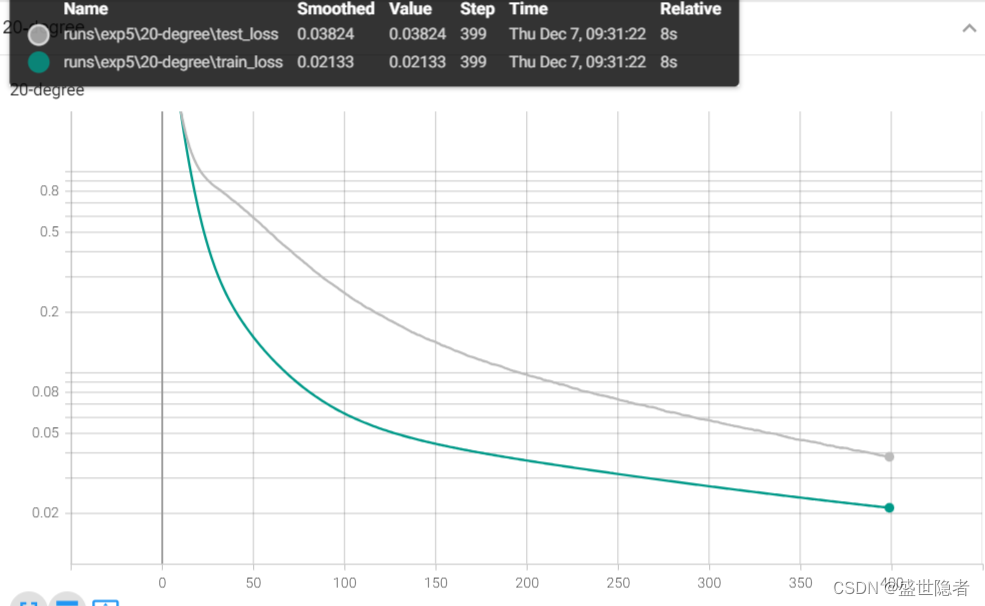
2.2.2. 输出结果

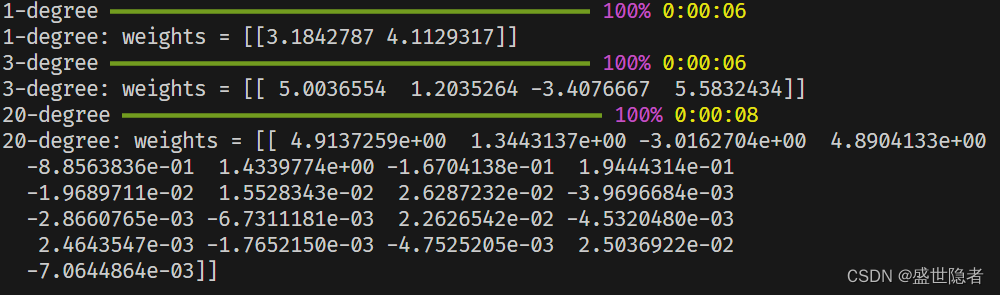
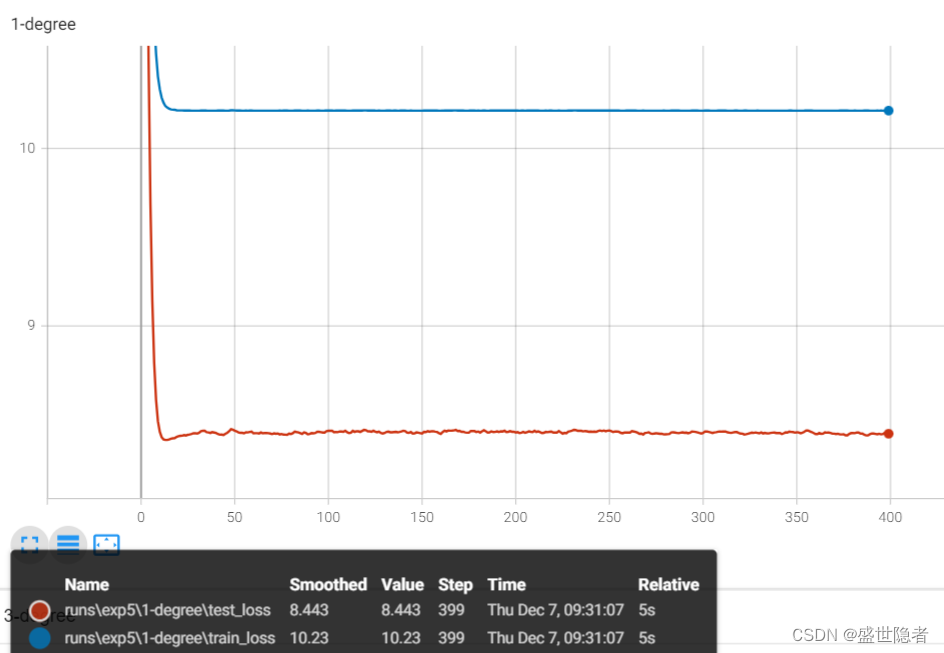
• 采用1阶多项式（线性模型）拟合
  
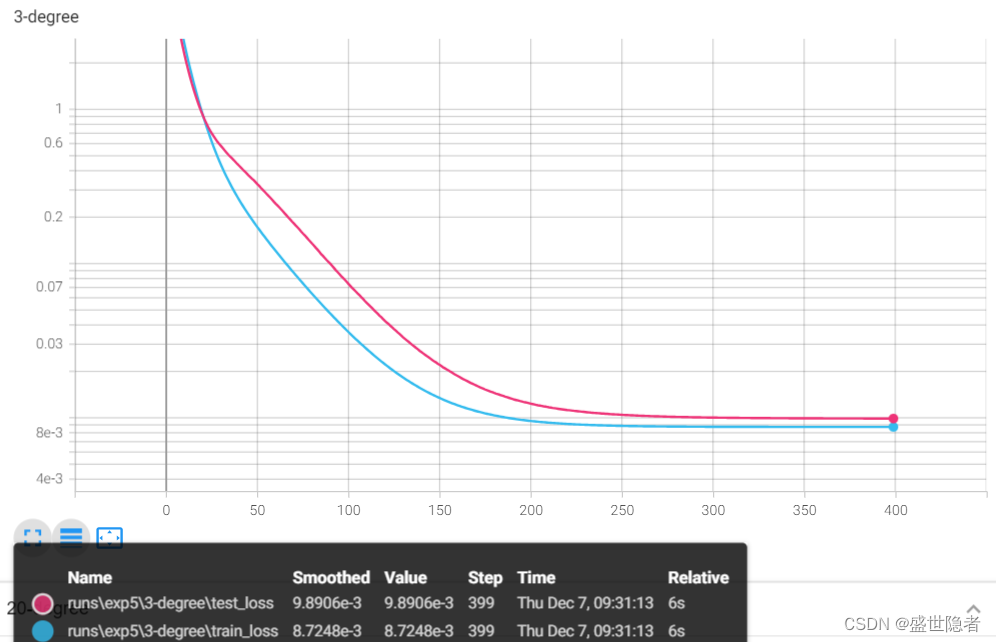
• 采用3阶多项式拟合
  
• 采用20阶多项式拟合