第4章 深度学习的数学基础

目录

4.7 指数函数和对数函数

4.7 指数函数和对数函数

深度学习经常会用到Sigmoid函数和Softmax函数，这些函数是通过包含exp(x)的指数函数创建的。后面我们需要求解这些函数的导数。

4.7.1 指数

指数是一个基于“乘以某个数多少次”，即乘法的次数的概念，并且不只是自然数，它还可以扩展到负数和实数。

图4-23 指数的定义与公式

指数函数的定义是：

$$y=a^x\text{\hspace{1em}(4-105)}$$

如果要强调指数函数中的$a$，那么可以称之为“以$a$为底数的指数函数”。这里的底数$a$是一个大于0且不等于1的数。

观察式4-105的图形可知（代码如下：），当a>1时，函数图形是单调递增的;当$0<a<1$时，图形是单调递减的。函数的输出总为正数。

# 代码清单 4-4-(1)
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inlinex = np.linspace(-4, 4, 100)
y = 2**x
y2 = 3**x
y3 = 0.5**xplt.figure(figsize=(5, 5))
plt.plot(x, y, 'black', linewidth=3, label='$y=2^x$')
plt.plot(x, y2, 'cornflowerblue', linewidth=3, label='$y=3^x$')
plt.plot(x, y3, 'gray', linewidth=3, label='$y=0.5^x$')
plt.ylim(-2, 6)
plt.xlim(-4, 4)
plt.grid(True)
plt.legend(loc='lower right')
plt.show()

输出结果：

图4-24 指数函数

指数具有以下性质，这些性质被称为指数法则：

$$a^b\cdot a^c=a^{b+c}$$

$$\frac{a^b}{a^c}=a^{b-c}$$

$${\left(a^b\right)}^c=a^{bc}$$

4.7.2 对数

对数的公式如图4-28所示。把指数函数的输入和输出反过来，就可以得到对数函数。也就是说，对数函数是指数函数的反函数。

图4-25 对数的定义与公式

思考下式：

$$x=a^y\text{\hspace{1em}(4-106)}$$

首先，把式4-106变形为“$y=$”的形式，得到：

$$y={\log }_{a}x\text{\hspace{1em}(4-107)}$$

绘制函数图形（代码如下：），式4-107与$y=a^x$的图形相对于$y=x$的直线相互对称。

# 代码清单 4-4-(2)
x = np.linspace(-8, 8, 100)
y = 2**x
z = np.zeros(100)x2 = np.linspace(0.001, 8, 100) # np.log(0)会导致出错，所以不能包含 0
y2 = np.log(x2) / np.log(2)# 通过公式 (7) 计算以 2 为底数的 logplt.figure(figsize=(5, 5))
plt.plot(x, y, 'black', linewidth=3)
plt.plot(x2, y2, 'cornflowerblue', linewidth=3)
plt.plot(x, x, 'black', linestyle='--', linewidth=1)
plt.plot(x, z, 'r',linewidth=1)
plt.plot(z, x, 'r',linewidth=1)
plt.ylim(-8, 8)
plt.xlim(-8, 8)
plt.grid(True)
plt.show()

输出结果：


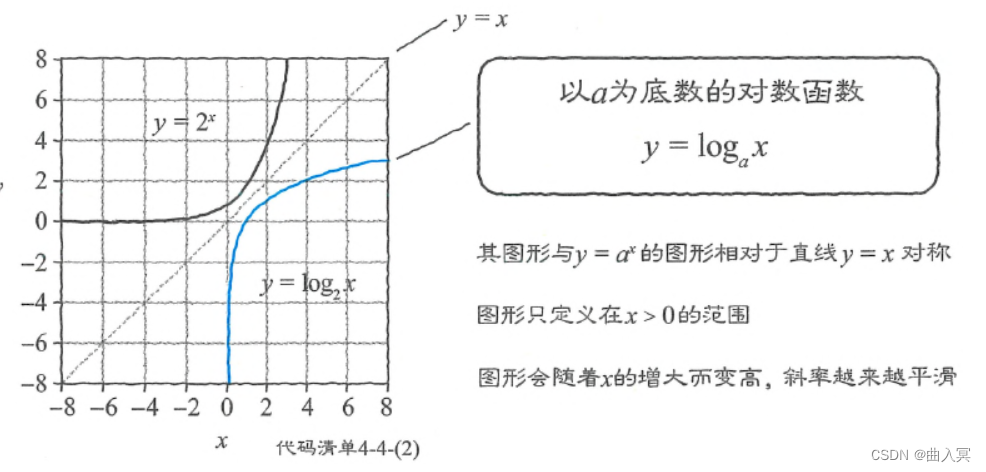
图4-26 对数函数

对数函数具体以下性质，称为对数运算法则：

$$\log ab=\log a+\log b$$

$$\log \frac{a}{b}=\log a-\log b$$

$$\log a^b=b\log a$$

$$\log \mathrm{e}=1$$

使用对数函数可以把过大或过小的数转为便于处理的大小。比如，$100000000=10^8$可以表示为$a=10$的对数，即${\log }_{10}10^8=8$，而$0.00000001=10^{-8}$可以表示为${\log }_{10}10^{-8}=-8$。

如果只写作$\log x$，不写出底数，则默认底数为$e$。$e$是一个为2.718…的无理数，又称为自然常数（自然对数的底数）或纳皮尔常数。

机器学习中经常出现非常大或非常小的数，在使用程序处理这些数时，可能会引起溢出（位数溢出）。对于这样的数，可以使用对数防止溢出。

此外，对数还可以把乘法运算转换为加法运算。对图4-28（4）进行扩展，可以得到：

$$\log \prod _{n=1}^{N}f(n)=\sum _{n=1}^N\log f(n)\text{\hspace{1em}(4-108)}$$

像这样转换之后，计算过程会更加轻松。因此，对于后面将会出现的似然这种以乘法运算形式表示的概率，往往会借助其对数，即似然对数来进行计算。

我们常常遇到“已知函数$f(x)$，求使$f(x)$最小的$x^{\ast }$”的情况。此时，其对数函数$\log f(x)$也在$x=x^{\ast }$时取最小值。对数函数是一个单调递增函数，所以即使最小值改变了，使函数取最小值的那个值也不会改变。这在求最大值时也成立。使$f(x)$取最大值的值也会使$f(x)$的对数函数取最大值。代码如下：

# 代码清单 4-4-(3)
x = np.linspace(-4, 4, 100)
y = (x - 1)**2 + 2
logy = np.log(y)plt.figure(figsize=(4, 4))
plt.plot(x, y, 'black', linewidth=3)
plt.plot(x, logy, 'cornflowerblue', linewidth=3)
plt.yticks(range(-4,9,1))
plt.xticks(range(-4,5,1))
plt.ylim(-4, 8)
plt.xlim(-4, 4)
plt.grid(True)
plt.show()

输出结果：

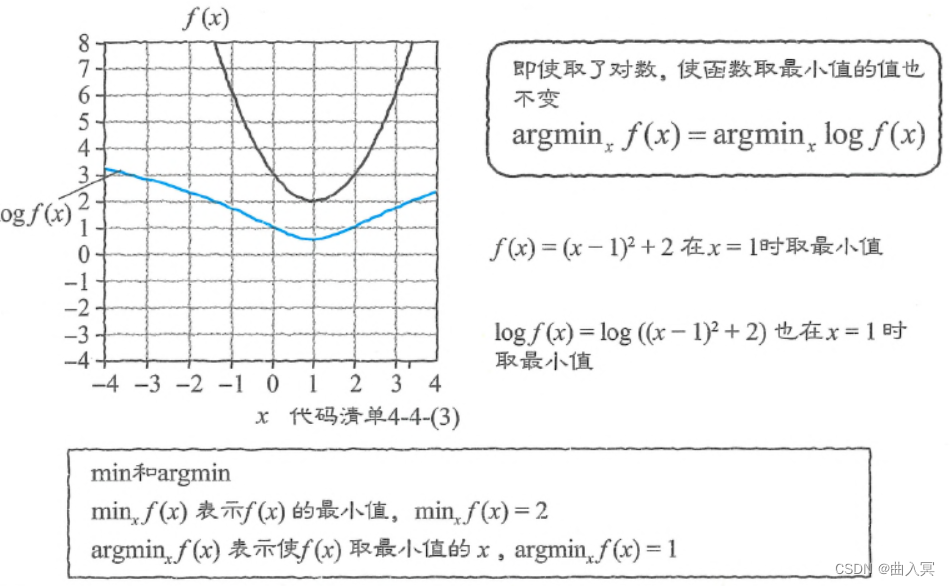
图4-27 对数函数取最小值的位置不变

鉴于这个性质，在求$f(x)$的最小值$x^{\ast }$时，我们经常通过$\log f(x)$求最小值$x^{\ast }$。特别是当$f(x)$以积的形式表示时，如式4-108所示，通过$\log$将其转换为和的形式，就会更容易求出导数，非常方便。

4.7.3 指数函数的导数

指数函数$y=a^x$对$x$的导数为：

$$y^{\prime }={\left(a^x\right)}^{\prime }=a^x\log a\text{\hspace{1em}(4-109)}$$

这里把$dy/dx$简单地表示为$y’$。函数$y=a^x$的导数是原本的函数式乘以$\log a$的形式。

设$a=2$，那么$\log 2$约为0.69，$y=a^x$的图形会稍微向下缩一些。

# 代码清单 4-4-(4)
x = np.linspace(-4, 4, 100)
a = 2
y = a**x
dy = np.log(a) * yplt.figure(figsize=(4, 4))
plt.plot(x, y, 'rosybrown', linestyle='--', linewidth=3)
plt.plot(x, dy, color='black', linewidth=3)
plt.ylim(-1, 8)
plt.xlim(-4, 4)
plt.grid(True)
plt.show()

输出结果：

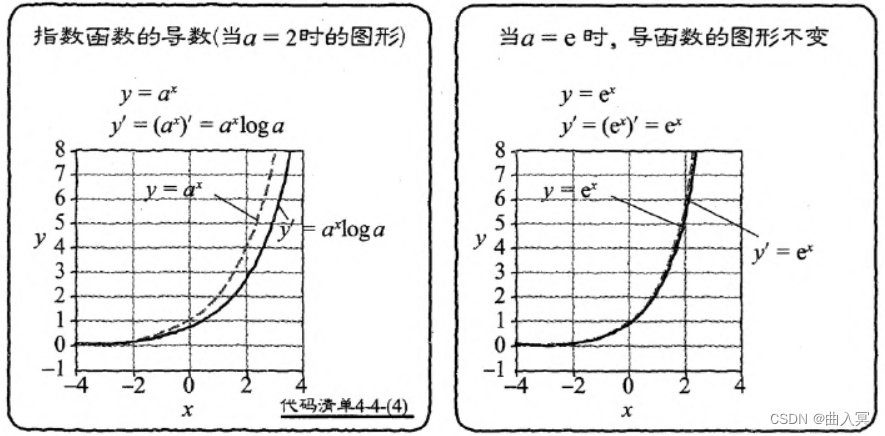
图4-28 指数函数的导数

这里有一个特殊情况，即当$a=e$时，$\log e=1$：

$$y^{\prime }={\left(e^x\right)}^{\prime }=e^x\text{\hspace{1em}(4-110)}$$

也就是说，当$a=e$时，导函数的图形不变（图4-28右）。这个性质在计算导数时特别方便。

因此，以$e$为底数的指数函数的应用很广泛，Sigmoid函数、Softmax函数和高斯函数也常常使用$e$。

4.7.4 对数函数的导数

对数函数的导数为反比例函数：

$$y^{\prime }=(\log x{)}^{\prime }=\frac{1}{x}\text{\hspace{1em}(4-111)}$$

代码如下：

# 代码清单 4-4-(5)
x = np.linspace(0.0001, 4, 100)  # 不能定义 0 以下
y = np.log(x)
dy = 1 / xplt.figure(figsize=(4, 4))
plt.plot(x, y, 'cyan', linestyle='--', linewidth=3)
plt.plot(x, dy, color='black', linewidth=3)
plt.ylim(-8, 8)
plt.xlim(-1, 4)
plt.grid(True)
plt.show()

输出结果：

图4-29 对数函数的导数

第7.1节会出现 { l o g ( 1 − x ) } ′ \{log(1-x)\}' {log(1−x)}′这样的导数，这里设$z=1-x$，$y=\log z$，然后，使用链式法则即可求出导数：

$$\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}y}{\mathrm{d}z}\cdot \frac{\mathrm{d}z}{\mathrm{d}x}=\frac{1}{z}\cdot (-1)=-\frac{1}{1-x}\text{\hspace{1em}(4-112)}$$

4.7.5 Sigmoid函数

Sigmoid函数是一个像平滑的阶梯一样的函数：

$$y=\frac{1}{1+{\mathrm{e}}^{-x}}\text{\hspace{1em}(4-113)}$$

$e^{-x}$也可以写作$exp(-x)$，所以Sigmoid函数有时也表示为：

$$y=\frac{1}{1+exp(-x)}\text{\hspace{1em}(4-114)}$$

这个函数的图形如图4-33所示，代码如下：

# 代码清单 4-4-(6)
x = np.linspace(-10, 10, 100)
y = 1 / (1 + np.exp(-x))
y1=np.zeros(100)
y2=np.ones(100)plt.figure(figsize=(4, 4))
plt.plot(x, y, 'black', linewidth=3)
plt.plot(x,y1,'r')
plt.plot(x,y2,c='violet')plt.ylim(-1, 2)
plt.xlim(-10, 10)
plt.grid(True)
plt.show()

输出结果：

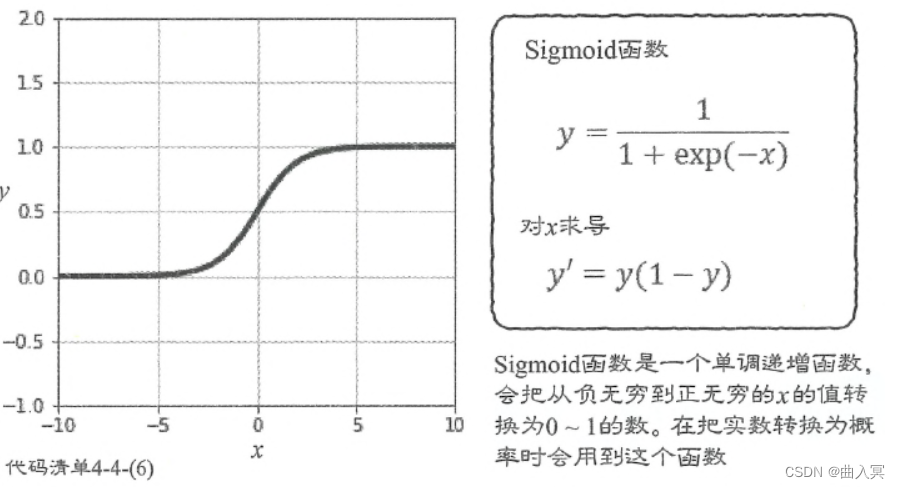
图4-30 Sigmoid函数

Sigmoid函数会把从负实数到正实数的数转换为0-1的数，所以常常用于表示概率。但这个函数并不是为了使输出范围为0-1而刻意创建的，而是基于一定的条件自然推导出来的。

Sigmoid函数在神经网络中是表示神经元的特性的重要函数。我们会用到Sigmoid函数的导数，所以这里先求一下它的导数。

先思考导数公式，为了使其与式4-113一致，这里设$f(x)=1+exp(-x)$：

$${\left(\frac{1}{f(x)}\right)}^{\prime }=-\frac{f^{\prime }(x)}{f(x{)}^2}\text{\hspace{1em}(4-115)}$$

$f(x)$的导数为$f^{\prime }(x)=-exp(-x)$，因此可得到：

$$\begin{gathered} y^{\prime }={\left(\frac{1}{1+\exp (-x)}\right)}^{\prime }= \\ -\frac{-\exp (-x)}{(1+\exp (-x){)}^2}=\frac{\exp (-x)}{(1+\exp (-x){)}^2}\text{\hspace{1em}(4-116)} \end{gathered}$$

对式4-116略微变形：

$$\begin{gathered} y^{\prime }=\frac{1}{1+\exp (-x)}\cdot \frac{1+\exp (-x)-1}{1+\exp (-x)}= \\ \frac{1}{1+\exp (-x)}\cdot \left\{1-\frac{1}{1+\exp (-x)}\right\}\text{\hspace{1em}(4-117)} \end{gathered}$$

这里，$1/(1+exp(-x))$就是$y$，所以可以用改写式子，改写后的式子非常简洁：

$$y^{\prime }=y(1-y)\text{\hspace{1em}(4-118)}$$

4.7.6 Softmax函数

已知$x_0=2$，$x_1=1$，$x_2=-1$，现在我们要保持这些数的大小关系不动，把它们转换为表示概率的$y_0$、$y_1$、$y_2$。既然是概率，就必须是0-1的数，而且所有数的和必须是1。

这时就需要用Softmax函数。首先，求出各个$x_i$的$exp$的和$u$：

$$u=\exp \left(x_0\right)+\exp \left(x_1\right)+\exp \left(x_2\right)\text{\hspace{1em}(4-119)}$$

使用式4-119，可以得到：

$$y_0=\frac{\exp \left(x_0\right)}{u},y_1=\frac{\exp \left(x_1\right)}{u},y_2=\frac{\exp \left(x_2\right)}{u}\text{\hspace{1em}(4-120)}$$

下面，我们实际编写代码创建Softmax函数，并测试：

# 代码清单 4-4-(7)
def softmax(x0, x1, x2):u = np.exp(x0) + np.exp(x1) + np.exp(x2)return np.exp(x0) / u, np.exp(x1) / u, np.exp(x2) / u# test
y = softmax(2, 1, -1)
print(np.round(y,2))  # (A) 显示小数点后两位的概率
print(np.sum(y))      # (B) 显示和

输出结果：

[0.71 0.26 0.04]
1.0

前面例子中的$x_0=2$，$x_1=1$，$x_2=-1$分别被转换为了$y_0=0.71$，$y_1=0.26$，$y_2=0.04$。可以看到，它们的确是按照原本的大小关系被分配了0-1的数，而且所有数相加之后的和为1。

Softmax函数的图形是什么样的呢？由于输入和输出都是三维的，所以不能直接绘制图形。因此，这里只固定$x_2=1$，然后把输入各种$x_0$和$x_1$之后得到的$y_0$和$y_1$展示在图形上。代码如下：

# 代码清单 4-4-(8)from mpl_toolkits.mplot3d import Axes3Dxn = 20
x0 = np.linspace(-4, 4, xn)
x1 = np.linspace(-4, 4, xn)y = np.zeros((xn, xn, 3))
for i0 in range(xn):for i1 in range(xn):y[i1, i0, :] = softmax(x0[i0], x1[i1], 1)xx0, xx1 = np.meshgrid(x0, x1)
plt.figure(figsize=(8, 3))
for i in range(2):ax = plt.subplot(1, 2, i + 1, projection='3d')ax.plot_surface(xx0, xx1, y[:, :, i], rstride=1,  cstride=1, alpha=0.3, color='blue', edgecolor='black')ax.set_xlabel('$x_0$', fontsize=14)ax.set_ylabel('$x_1$', fontsize=14)ax.view_init(40, -125)plt.show()

输出结果：

图4-31 Softmax函数

把$x_2$固定为1，再令$x_0$和$x_1$变化之后，$y_0$、$y_1$的值会在0-1的范围内变化（图4-31左）。$x_0$越大，$y_0$越趋近于1；$x_1$越大，$y_1$越趋近于1。图中没有显示$y_2$，不过$y_2$是1减去$y_0$和$y_1$得到的差，所以应该可以想象到$y_2$是什么样的。

Softmax函数不仅可以用在包含三个变量的情况中，也可以用在包含更多变量的情况中。设变量的数量为$K$，Softmax函数可以表示为：

$$y_i=\frac{\exp \left(x_i\right)}{{\sum }_{j=0}^{K-1}\exp \left(x_j\right)}\text{\hspace{1em}(4-121)}$$

Softmax函数的偏导数将在随后章节出现，这里先求一下。首先，求$y_0$对$x_0$的偏导数：

$$\frac{\partial y_0}{\partial x_0}=\frac{\partial }{\partial x_0}\frac{\exp \left(x_0\right)}{u}\text{\hspace{1em}(4-122)}$$

这里必须要注意，$u$也是关于$x_0$的函数。因此，需要使用导数公式，设：

$$f(x)=u=exp(x_0)+exp(x_1)+exp(x_2),g(x)=exp(x_0)$$

则：

$${\left(\frac{g(x)}{f(x)}\right)}^{\prime }=\frac{g^{\prime }(x)f(x)-g(x)f^{\prime }(x)}{f(x{)}^2}\text{\hspace{1em}(4-123)}$$

推导过程：

$$(fg{)}^{\prime }=f^{\prime }g+f{g}^{\prime }$$

分析：

例如：$x\times \sin x$的导数等于$x$的导数乘以$\sin x$加$x$乘以$\sin x$的导数。等于$1\times \sin x+x\times \cos x$。

扩展资料：

商的导数公式：

$$(u/v{)}^{\prime }=(u{v}^{-1}{)}^{\prime }$$
$$=u^{\prime }(v^{-1})+(v^{-1}{)}^{\prime }u$$
$$=u^{\prime }(v^{-1})+(-1)v^{-2}u$$
$$=u^{\prime }/v-u{v}^{\prime }/(v^2)$$

通分，易得：
$$(u/v)=(u^{\prime }v-u{v}^{\prime })/v^2$$

这里以$f^{\prime }(x)=\partial f/\partial x_0,g^{\prime }(x)=\partial g/\partial x_0$思考：

$$\begin{array}{l}{f}^{\prime }(x)=\frac{\partial }{\partial x_0}f(x)=\exp \left(x_0\right)\\ g^{\prime }(x)=\frac{\partial }{\partial x_0}g(x)=\exp \left(x_0\right)\end{array}\text{\hspace{1em}(4-124)}$$

因此，式4-123可变形为：

$$\begin{array}{rl}\frac{\partial y_0}{\partial x_0}={\left(\frac{g(x)}{f(x)}\right)}^{\prime }& =\frac{\exp \left(x_0\right)u-\exp \left(x_0\right)\exp \left(x_0\right)}{u^2}\\ & =\frac{\exp \left(x_0\right)}{u}\left(\frac{u-\exp \left(x_0\right)}{u}\right)\\ & =\frac{\exp \left(x_0\right)}{u}\left(\frac{u}{u}-\frac{\exp \left(x_0\right)}{u}\right)\end{array}\text{\hspace{1em}(4-125)}$$

这里使用$y_0=exp(x_0)/u$，将式4-125表示为：

$$\frac{\partial y_0}{\partial x_0}=y_0(1-y_0)\text{\hspace{1em}(4-126)}$$

令人震惊的是，上式的形式竟然跟Sigmoid函数的导数公式（式4-118）完全相同。

$$y^{\prime }=y(1-y)\text{\hspace{1em}(4-118)}$$

接下来，我们求$y_0$对$x_1$的偏导数：

$$\frac{\partial y_0}{\partial x_1}=\frac{\partial }{\partial x_1}\frac{\exp \left(x_0\right)}{u}\text{\hspace{1em}(4-127)}$$

这里也设$f(x)=u=exp(x_0)+exp(x_1)+exp(x_2),g(x)=exp(x_0)$，并使用公式4-123：

$${\left(\frac{g(x)}{f(x)}\right)}^{\prime }=\frac{g^{\prime }(x)f(x)-g(x)f^{\prime }(x)}{f(x{)}^2}\text{\hspace{1em}(4-123)}$$

设 $f^{\prime }(x)=\partial f/\partial x_1,g^{\prime }(x)=\partial g/\partial x_1$，思考如何对$x_1$求偏导数：

$$\begin{array}{l}{f}^{\prime }(x)=\frac{\partial }{\partial x_1}f(x)=\exp \left(x_1\right)\\ g^{\prime }(x)=\frac{\partial }{\partial x_1}\exp \left(x_0\right)=0\end{array}$$

结果为：

$$\begin{array}{rl}\frac{\partial y_0}{\partial x_1}& =\frac{g^{\prime }(x)f(x)-g(x)f^{\prime }(x)}{f(x{)}^2}=\frac{-\exp \left(x_0\right)\exp \left(x_1\right)}{u^2}\\ & =-\frac{\exp \left(x_0\right)}{u}\cdot \frac{\exp \left(x_1\right)}{u}\end{array}\text{\hspace{1em}(4-128)}$$

这里使用$y_0=exp(x_0)/u$，$y_1=exp(x_1)/u$，可得到：

$$\frac{\partial y_0}{\partial x_1}=-y_0{y}_1\text{\hspace{1em}(4-129)}$$

综合式4-126：

$$\frac{\partial y_0}{\partial x_0}=y_0(1-y_0)\text{\hspace{1em}(4-126)}$$

和式4-129并加以拓展，得到：

$$\frac{\partial y_j}{\partial x_i}=y_j\left(I_{ij}-y_i\right)\text{\hspace{1em}(4-130)}$$

这里，$I_{ij}$是一个在$i=j$时为1，在$i\ne j$时为0的函数。$I_{ij}$也可以表示为称为克罗内克函数。

4.7.7 Softmax函数和Sigmoid函数

Softmax函数和Sigmoid函数是非常相似的。这两个函数有什么关系呢？下面我们试着思考一下。一个包含两个变量的Softmax函数是：

$$y=\frac{{\mathrm{e}}^{x_0}}{{\mathrm{e}}^{x_0}+{\mathrm{e}}^{x_1}}\text{\hspace{1em}(4-131)}$$

将分子和分母均乘以$e^{-x_0}$。并整理，再使用公式$e^a{e}^{-b}=e^{a-b}$，可以得到：

$$y=\frac{{\mathrm{e}}^{x_0}{\mathrm{e}}^{-x_0}}{{\mathrm{e}}^{x_0}{\mathrm{e}}^{-x_0}+{\mathrm{e}}^{x_1}{\mathrm{e}}^{-x_0}}=\frac{{\mathrm{e}}^{x_0-x_0}}{{\mathrm{e}}^{x_0-x_0}+{\mathrm{e}}^{x_1-x_0}}=\frac{1}{1+{\mathrm{e}}^{-\left(x_0-x_1\right)}}\text{\hspace{1em}(4-132)}$$

这里代入$x=x_0-x_1$，可以得到Sigmoid函数：

$$y=\frac{1}{1+e^{-x}}\text{\hspace{1em}(4-133)}$$

也就是说，把包含两个变量的Softmax函数的输入$x_0$和$x_1$，用它们的差$x=x_0-x_1$表示，就可以得到Sigmoid函数。也可以说，把Sigmoid函数扩展到多个变量之后得到的就是Softmax函数。

4.7.8 高斯函数

高斯函数可表示为：

$$y=exp(-x^2)\text{\hspace{1em}(4-134)}$$

如图4-32左图中的黑线所示，高斯函数的图形以$x=0$为中心，呈吊钟形。

图4-32高斯函数

用$\mu$表示这个函数图形的中心（均值），用$\sigma$表示分布的幅度（标准差），用$a$表示高度，则高斯函数为（图4-32左图中的灰线）：

$$y=a\exp \left(-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right)\text{\hspace{1em}(4-135)}$$

下面尝试绘制它的图形，代码如下：

# 代码清单 4-4-(9)
def gauss(mu, sigma, a):return a * np.exp(-(x - mu)**2 / (2 * sigma**2))x = np.linspace(-4, 4, 100)
plt.figure(figsize=(4, 4))
plt.plot(x, gauss(0, 1, 1), 'black', linewidth=3)
plt.plot(x, gauss(2, 2, 0.5), 'gray', linewidth=3)
plt.ylim(-.5, 1.5)
plt.xlim(-4, 4)
plt.grid(True)
plt.show()

输出结果：

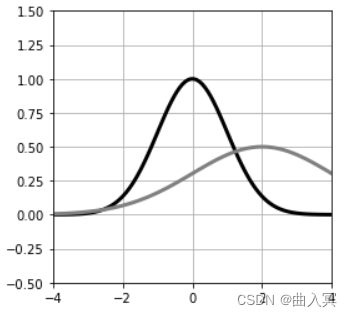
高斯函数有时会用于表示概率分布，在这种情况下，要想使得对$x$求积分的值为1，就需要令式4-135中的$a$为：

$$a=\frac{1}{{\left(2\pi {\sigma }^2\right)}^{1/2}}\text{\hspace{1em}(4-136)}$$

4.7.9 二维高斯函数

高斯函数可以扩展到二维。二维高斯函数将在混合高斯模型中出现。
设输入是二维向量$\mathbf{x}=[x_0,x_1{]}^T$，则高斯函数的基本形式为：

$$y=\exp \left\{-\left(x_0^2+x_1^2\right)\right\}\text{\hspace{1em}(4-137)}$$

二维高斯函数的图形如图4-33所示，形似一个以原点为中心的同心圆状的吊钟。

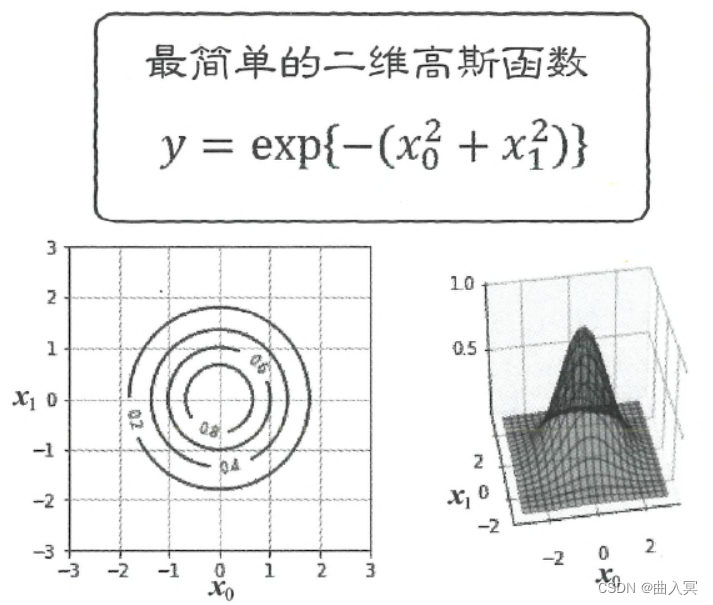
图4-33 一个简单的二维高斯函数

在此基础上，为了能够移动其中心，或使其变细长，这里添加几个参数，得到：

$$y=a\cdot \exp \left\{-\frac{1}{2}(\mathbf{x}-\mathbf{\mu }{)}^{\mathrm{T}}{\Sigma }^{-1}(\mathbf{x}-\mathbf{\mu })\right\}\text{\hspace{1em}(4-138)}$$

如此一来，$exp$中就会有向量或矩阵，下面逐个介绍。

首先，参数$\mu$和$\Sigma$表示的是函数的形状。$\mu$是均值向量（中心向量），表示函数分布的中心：

$$\mathbf{\mu }={\left[\begin{array}{ll}{\mu }_0& {\mu }_1\end{array}\right]}^{\mathrm{T}}\text{\hspace{1em}(4-139)}$$

$\Sigma$被称为协方差矩阵，是一个如下所示的$2\times 2$矩阵：

$$\Sigma =\left[\begin{array}{cc}{\sigma }_0^2& {\sigma }_{01}\\ {\sigma }_{01}& {\sigma }_1^2\end{array}\right]\text{\hspace{1em}(4-140)}$$

我们可以给矩阵中的元素${\sigma }_0^2$和${\sigma }_1^2$赋一个正值，分别用于调整$x_0$方向和$x_1$方向的函数分布的幅度。对于${\sigma }_{01}$，则赋一个正的或负的实数，用于调整函数分布方向上的斜率。如果是正数，那么函数图形呈向右上方倾斜的椭圆状；如果是负数，则呈向左上方倾斜的椭圆状（设$x_0$为横轴，$x_1$为纵轴时的情况）。

虽然我们往式4-138的$exp$中引入的是向量和矩阵，但变形之后却会变为标量。简单起见，我们设$\mathbf{\mu }=[{\mu }_0,{\mu }_1{]}^T=[0,0{]}^T$，然后试着计算$(\mathbf{x}-\mathbf{\mu }{)}^T{\sum }^{-1}(\mathbf{x}-\mathbf{\mu })$，可知$exp$中的值是一个由$x_0$和$x_1$构成的二次表达式：

$$\begin{array}{l}(\mathbf{x}-\mathbf{\mu }{)}^{\mathrm{T}}{\mathbf{\Sigma }}^{-1}(\mathbf{x}-\mathbf{\mu })={\mathbf{x}}^{\mathrm{T}}{\mathbf{\Sigma }}^{-1}\mathbf{x}\\ =\left[\begin{array}{ll}{x}_0& x_1\end{array}\right]\cdot \frac{1}{{\sigma }_0^2{\sigma }_1^2-{\sigma }_{01}^2}\left[\begin{array}{cc}{\sigma }_1^2& -{\sigma }_{01}\\ -{\sigma }_{01}& {\sigma }_0^2\end{array}\right]\left[\begin{array}{l}{x}_0\\ x_1\end{array}\right]\\ =\frac{1}{{\sigma }_0^2{\sigma }_1^2-{\sigma }_{01}^2}\left({\sigma }_1^2{x}_0^2-2{\sigma }_{01}{x}_0{x}_1+{\sigma }_0^2{x}_1^2\right)\end{array}\text{\hspace{1em}(4-141)}$$

$a$也可以看作一个控制函数大小的参数，当用在二维高斯函数中表示概率分布时，我们将其设为：

$$a=\frac{1}{2\pi }\frac{1}{|\Sigma {|}^{1/2}}\text{\hspace{1em}(4-142)}$$

在进行如上所示的变形后，输入空间的积分值为1，函数可以表示概率分布。

式4-142中的$|\Sigma |$是一个被称为“$\Sigma$的矩阵式”的量（把矩阵看作向量，行列式相当于向量的模），当矩阵大小为$2\times 2$时，$|\Sigma |$的值为：

$$|\mathbf{A}|=\left|\begin{array}{ll}a& b\\ c& d\end{array}\right|=ad-cb\text{\hspace{1em}(4-143)}$$

因此，$|\Sigma |$可以表示为：

$$|\Sigma |={\sigma }_0^2{\sigma }_1^2-{\sigma }_{01}^2\text{\hspace{1em}(4-144)}$$

下面通过Python程序绘制一下函数图形，代码如下：
$$y=a\cdot \exp \left\{-\frac{1}{2}(\mathbf{x}-\mathbf{\mu }{)}^{\mathrm{T}}{\Sigma }^{-1}(\mathbf{x}-\mathbf{\mu })\right\}\text{\hspace{1em}(4-138)}$$

$$a=\frac{1}{2\pi }\frac{1}{|\Sigma {|}^{1/2}}\text{\hspace{1em}(4-142)}$$

# 代码清单 4-5-(1)
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
%matplotlib inline# 高斯函数 -----------------------------
def gauss(x, mu, sigma):N, D = x.shapec1 = 1 / (2 * np.pi)**(D / 2)c2 = 1 / (np.linalg.det(sigma)**(1 / 2))  # np.linalg.det()：矩阵求行列式（标量）inv_sigma = np.linalg.inv(sigma)           # np.linalg.inv()：矩阵求逆c3 = x - muc4 = np.dot(c3, inv_sigma)c5 = np.zeros(N)for d in range(D):c5 = c5 + c4[:, d] * c3[:, d]p = c1 * c2 * np.exp(-c5 / 2)return p

输入数据$x$是$N\times 2$矩阵，mu是模为2的向量，sigma是$2\times 2$矩阵。下面代入适当的数值测试一下gauss(s, mu, sigma)。

# 代码清单 4-5-(2)
x = np.array([[1, 2], [2, 1], [3, 4]])
mu = np.array([1, 2])
sigma = np.array([[1, 0], [0, 1]])
print(gauss(x, mu, sigma))

由上面的结果可知，函数返回了与代入的三个数值相应的返回值。绘制该函数的等高线图形和三维图形的代码如代码如下：

# 代码清单 4-5-(3)
X_range0=[-3, 3]
X_range1=[-3, 3]# 显示等高线 --------------------------------
def show_contour_gauss(mu, sig):xn = 40  # 等高线的分辨率x0 = np.linspace(X_range0[0], X_range0[1], xn)x1 = np.linspace(X_range1[0], X_range1[1], xn)xx0, xx1 = np.meshgrid(x0, x1)x = np.c_[np.reshape(xx0, xn * xn, order='F'), np.reshape(xx1, xn * xn, order='F')]f = gauss(x, mu, sig)f = f.reshape(xn, xn)f = f.Tcont = plt.contour(xx0, xx1, f, 15, colors='k')plt.grid(True)# 三维图形 ----------------------------------
def show3d_gauss(ax, mu, sig):xn = 40  # 等高线的分辨率x0 = np.linspace(X_range0[0], X_range0[1], xn)x1 = np.linspace(X_range1[0], X_range1[1], xn)xx0, xx1 = np.meshgrid(x0, x1)x = np.c_[np.reshape(xx0, xn * xn, order='F'), np.reshape(xx1, xn * xn, order='F')]f = gauss(x, mu, sig)f = f.reshape(xn, xn)f = f.Tax.plot_surface(xx0, xx1, f, rstride=2, cstride=2, alpha=0.3, color='blue', edgecolor='black')# 主处理 -----------------------------------
mu = np.array([1, 0.5])            # (A)
sigma = np.array([[2, 1], [1, 1]]) # (B)Fig = plt.figure(1, figsize=(7, 3))
Fig.add_subplot(1, 2, 1)
show_contour_gauss(mu, sigma)
plt.xlim(X_range0)
plt.ylim(X_range1)
plt.xlabel('$x_0$', fontsize=14)
plt.ylabel('$x_1$', fontsize=14)Ax = Fig.add_subplot(1, 2, 2, projection='3d')
show3d_gauss(Ax, mu, sigma)
Ax.set_zticks([0.05, 0.10])
Ax.set_xlabel('$x_0$', fontsize=14)
Ax.set_ylabel('$x_1$', fontsize=14)
Ax.view_init(40, -100)
plt.show()

输出结果：

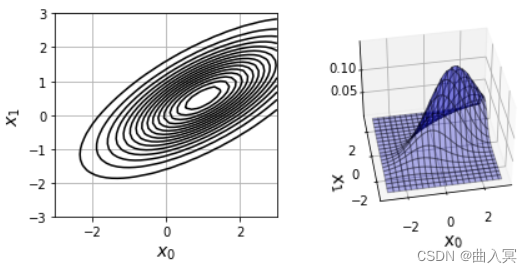
运行程序之后，可以得到如图4-37所示的图形。图形分布的中心为程序设定的中心，位于(1, 0.5)((A))。此外，由于${\sigma }_{01}=1$，所以图形分布呈向右上倾斜的形状（（$B$））。

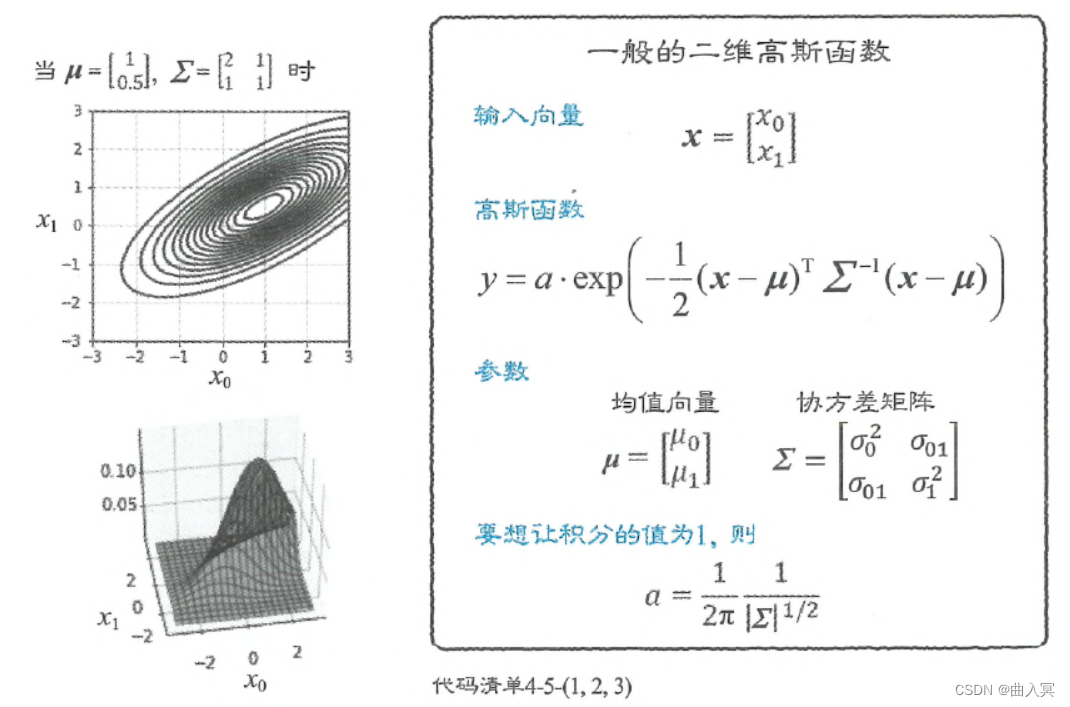
图4-34—般的二维高斯函数