代码的使用说明
【MATLAB】基于SVMD去噪的信号去噪算法(基础版)
代码的原理
1.SVMD原理
连续变分模式分解(Successive Variational Mode Decomposition,SVMD)是一种用于将混合信号根据其频率特性分离成各个独立分量的数据分析技术。它是变分模式分解(Variational Mode Decomposition,VMD)方法的一种扩展。
SVMD采用迭代的方法将信号分解为一组内禀模态函数(Intrinsic Mode Functions,IMFs),用于表示信号的不同频率分量或模式。通过求解一个最小化模式之间交叉干扰的优化问题,可以获得IMFs。
SVMD算法开始时,使用一组初始IMFs初始化分解过程。然后,通过交替更新IMFs和估计剩余信号来进行迭代,直到达到收敛。更新后的IMFs捕捉了信号的目标模式,而剩余部分表示无法进一步分解的信号成分。
SVMD相对于传统分解方法的优势在于其能够处理具有时变频率分量的非平稳信号。它可以有效地分离具有复杂谱内容或瞬态行为的信号。
SVMD在信号处理、生物医学工程、环境监测和振动分析等各个领域都有应用。它已被证明在从具有重叠频率分量或非线性动力学的信号中提取相关信息方面非常有用。
2.SVMD去噪原理
SVMD在信号去噪方面也有应用。通过分解信号成分,SVMD可以将噪声与信号分离,并抑制噪声分量。
下面是使用SVMD进行信号去噪的一般步骤:
- 数据准备:将带有噪声的原始信号准备好,确保信号是离散的,并具有足够的采样点数。
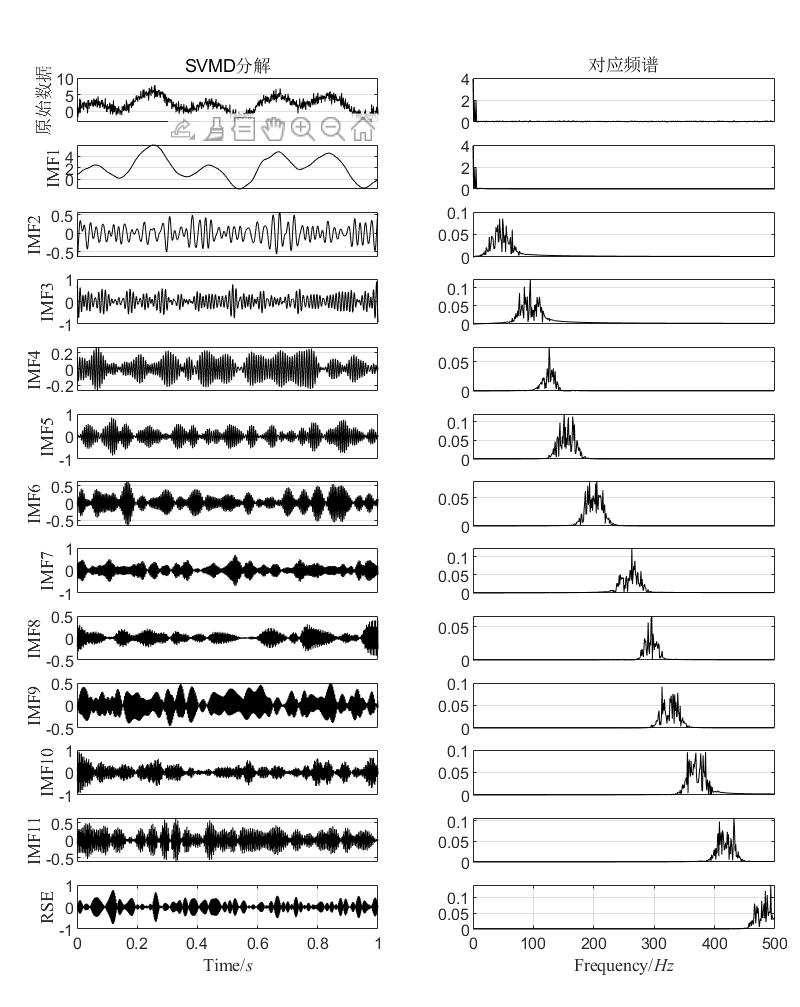
- SVMD分解:使用SVMD算法对原始信号进行分解,得到一组IMFs。这些IMFs代表了信号在不同频率上的分量。
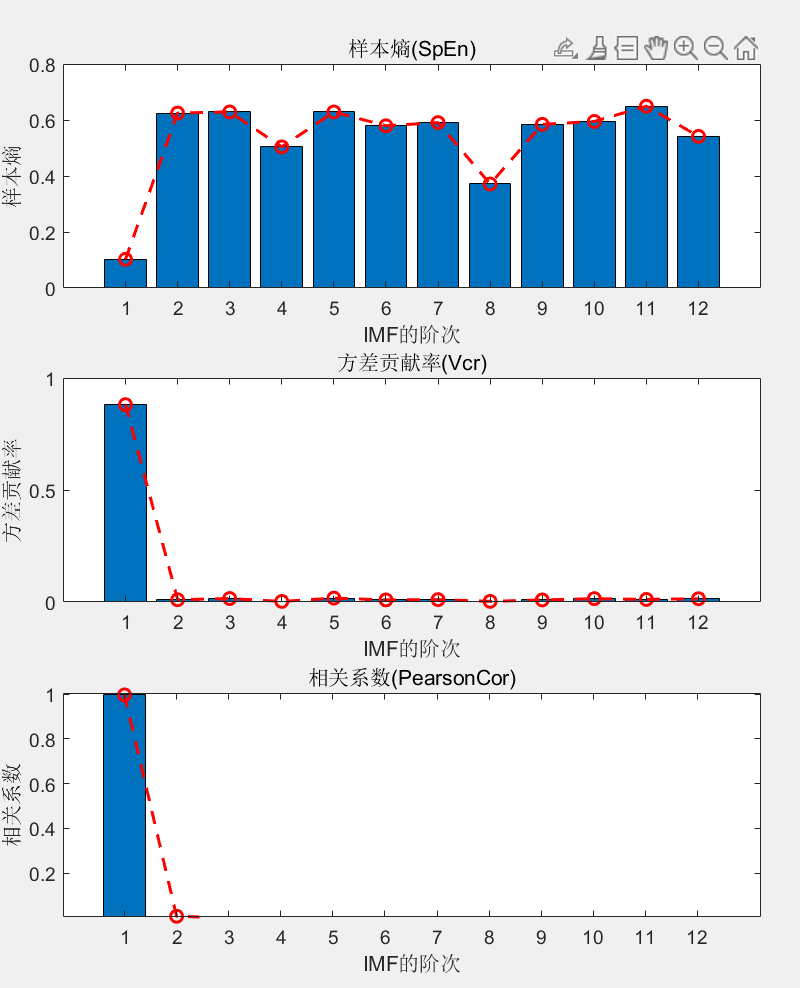
- 噪声分量识别:通过观察分解后的IMFs,识别哪些IMFs包含主要的噪声分量。通常,噪声分量具有较高的频率或较低的能量。选择包含噪声的IMFs。
- 去除噪声:去除步骤3中选定的包含噪声的IMFs,可以选择删除这些IMFs或将它们置为零。此步骤将直接影响信号去噪的效果。
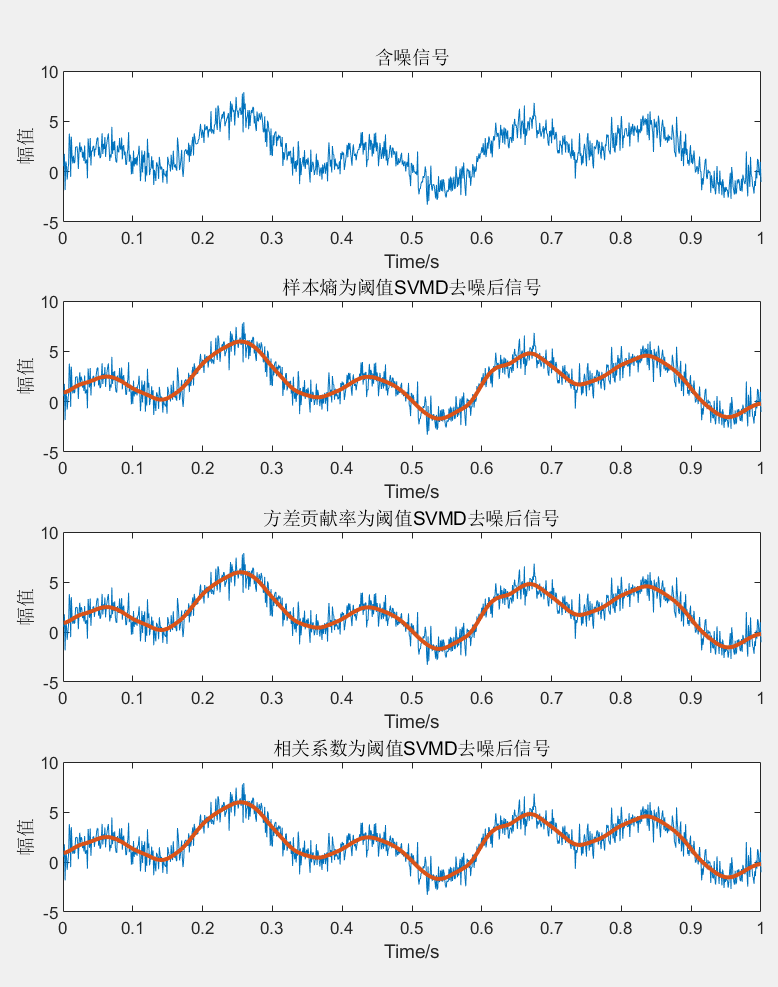
- 重构信号:将经过去除噪声的IMFs与保留的IMFs进行重构,得到经过去噪处理后的信号。
需要注意的是,在进行SVMD去噪时,对于不同的信号和噪声特性,可能需要调整算法的参数和去噪的策略。此外,选择合适的阈值或规则来界定哪些IMFs包含噪声和信号也是一个关键的步骤。
最佳的去噪效果可能需要反复尝试和优化。因此,建议根据具体的应用情况和需求,进行实验和参数调整,以获得最佳的信号去噪结果。
代码的流程图
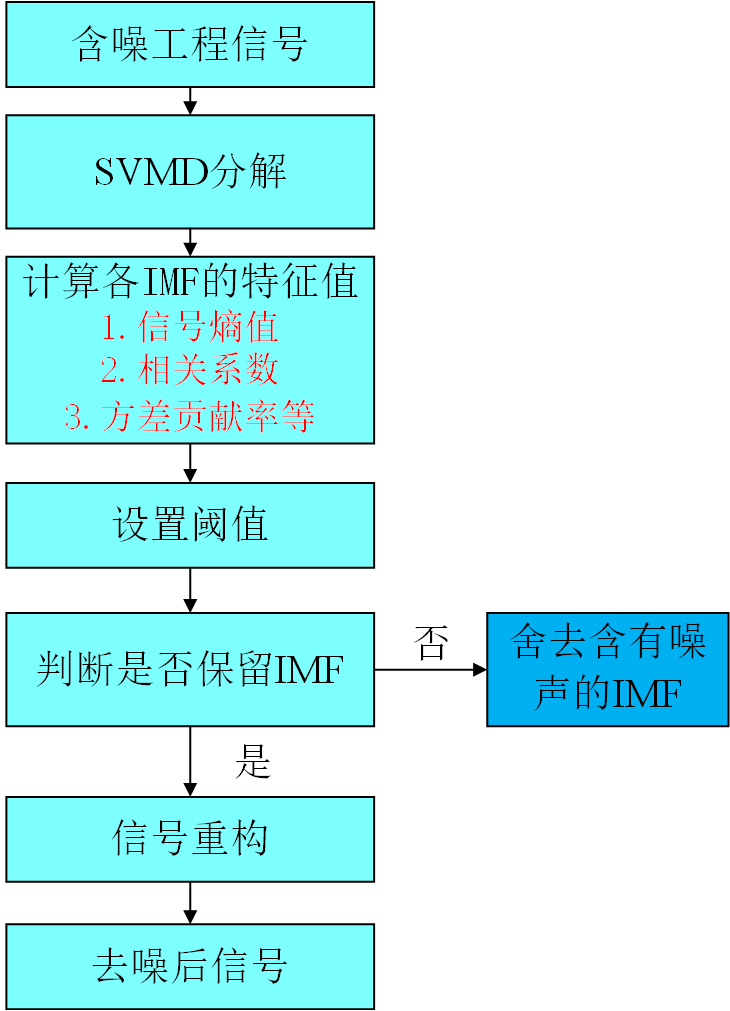
代码的效果图
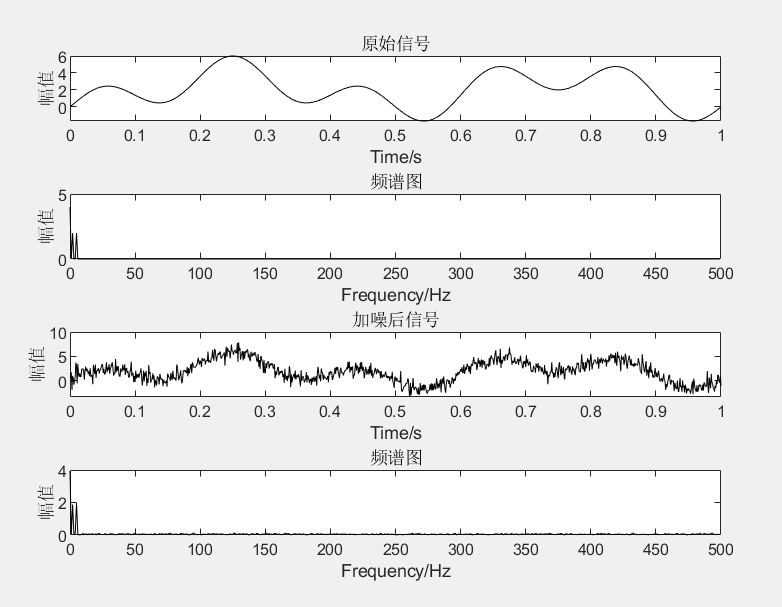
代码链接:https://www.alipan.com/s/W4Sms8oiXLC
获取代码请关注MATLAB科研小白的个人公众号(即文章下方二维码),并回复SVMD去噪
本公众号致力于解决找代码难,写代码怵。各位有什么急需的代码,欢迎后台留言~不定时更新科研技巧类推文,可以一起探讨科研,写作,文献,代码等诸多学术问题,我们一起进步。