未分配的题目
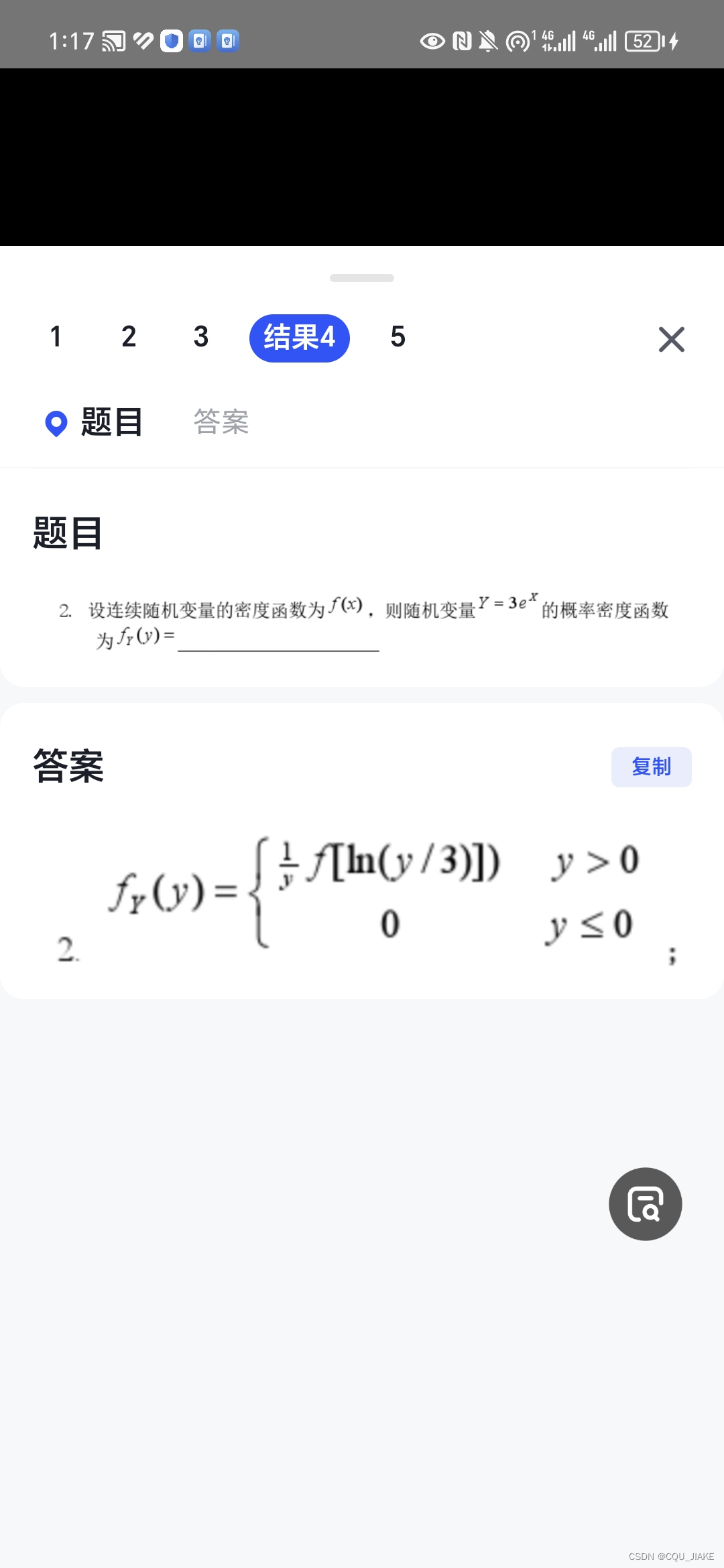
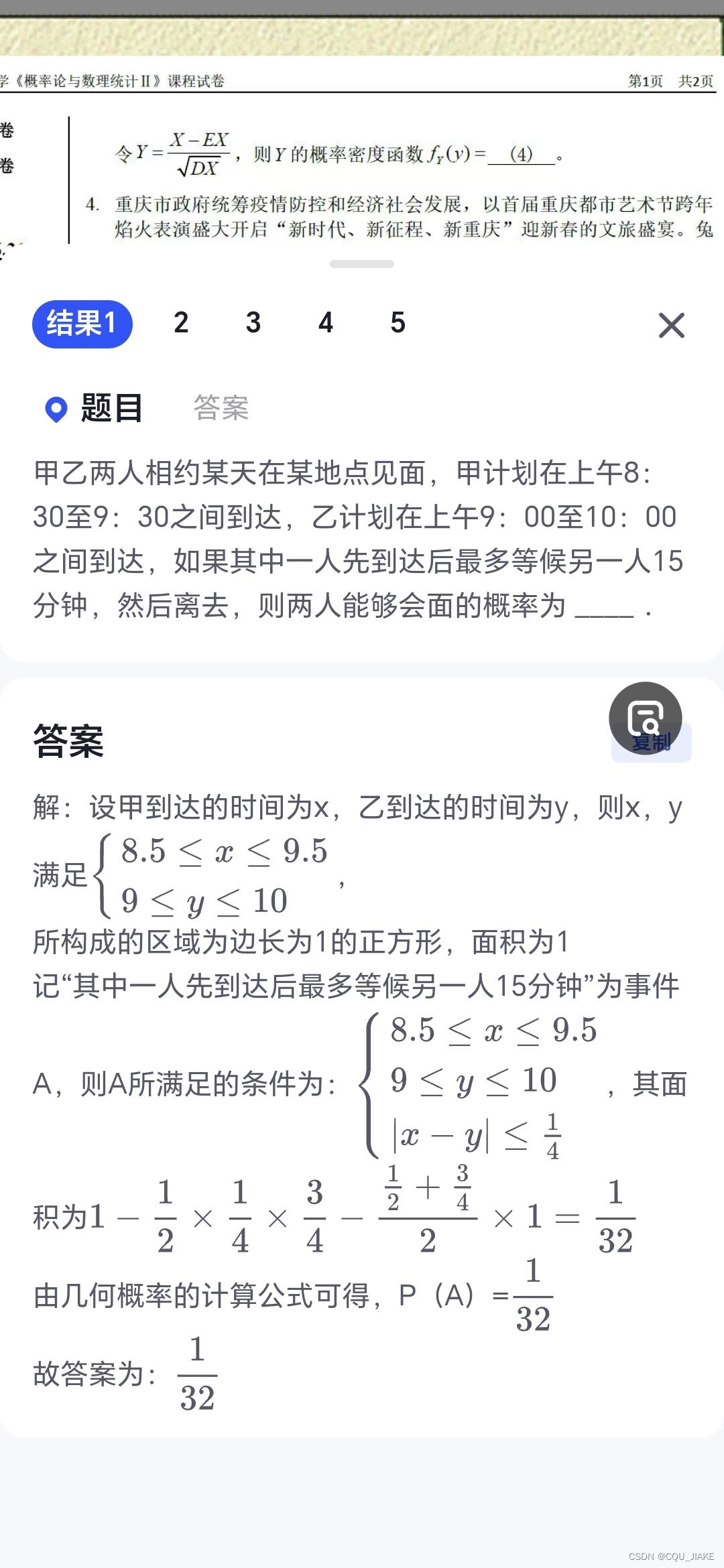




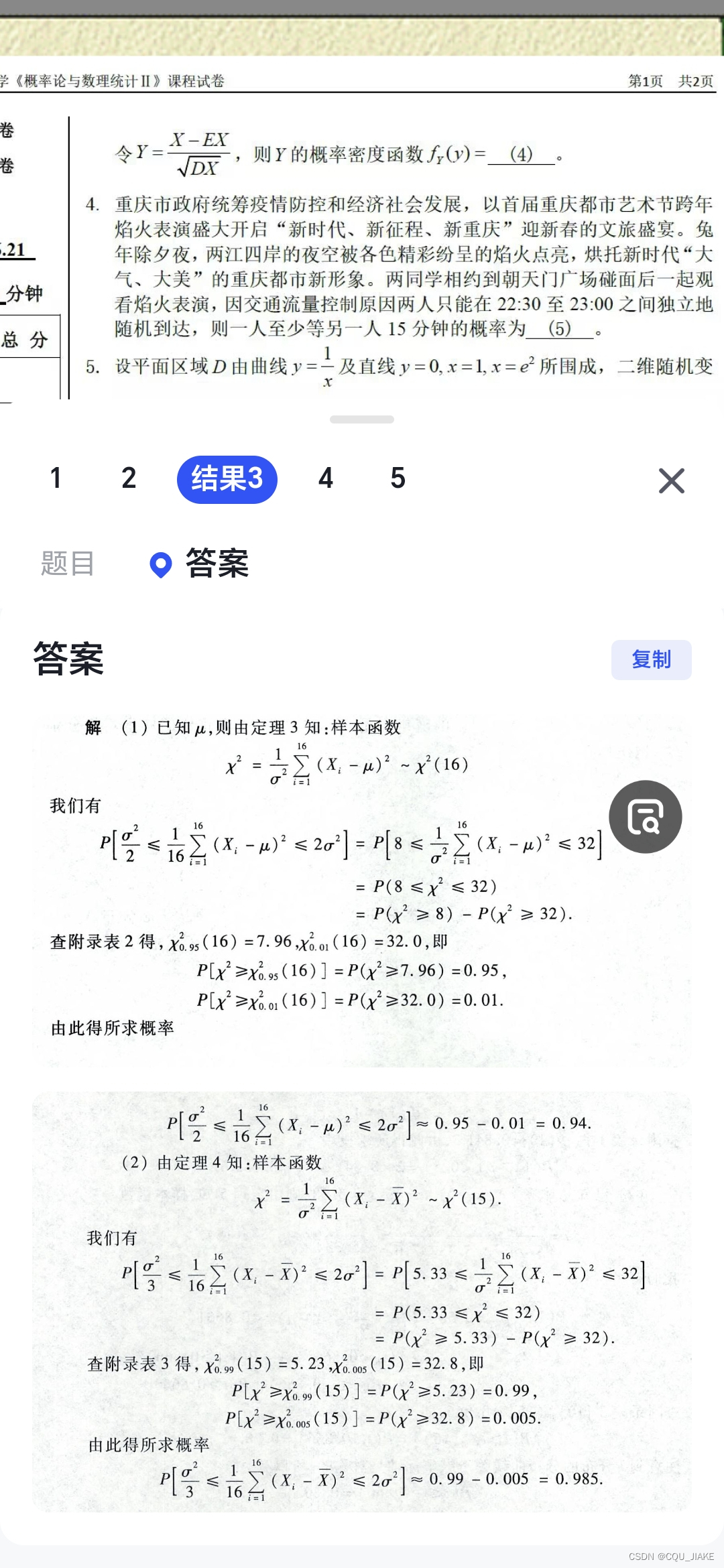




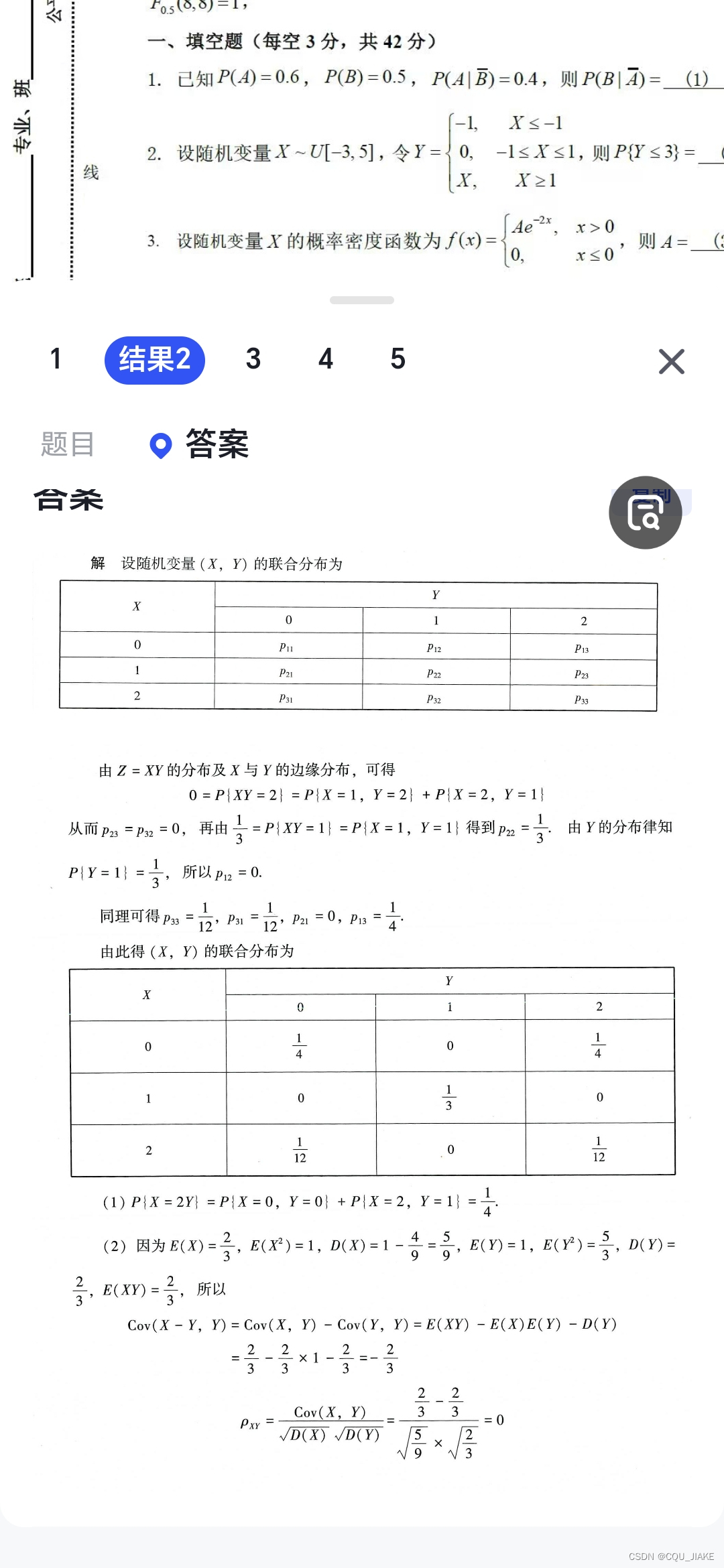




概率计算(一些转换公式与全概率公式)与实际概率 ,贝叶斯
一些转换公式











相关性质计算
常规,公式的COV与P
复习相关公式

计算出新表达式的均值,方差,再套正态分布的公式
![]()
COV的运算性质
如果两变量独立,那么EXY=EXEY
算COVXY,就是EXY-EXEY

E(X[X]),对于带绝对值的均值,直接进行积分,利用积分的对称关系求解
期望表达式中的式子,就是每个点对应的函数式的值。

面积为ΠR^2,派为常数,所以面积的期望取决于X^2的期望,方差取决于X^2的方差
COV(S,C)最终可化简为COV(R,R^2)=E(R*R^2)-E(R)E(R^2)
X^2的方差,计算一下X^4的积分,一共要算X^3,X^4两个积分

对于此类型的X,Y变化,满足变化后的量,均值为0,方差为1
奇怪,不规则的COV,P
一般就是离散的二维变量X,Y。核心就是依据题目特点,写出X,Y的离散分布表,然后就计算,EXY,EX,EY,EX^2,EY^2,DX,DY等关键数据
即主要是考分布律的求解


联合分布律,直接联合各变量可能出现的所有离散值列表,然后分别计算格子上各种情况的概率,就变得一目了然了

直接依照各变量可能取值列表,然后明确每个格子所代表的实际含义,再进行概率计算即可

标准差等的均值,方差性质
样本均值就是分布均值,与取样数量N无关;样本方差为分布方差除以N。
样本均值的均值是分布均值。
样本方差
样本均值为X拔,样本均值的均值就是总体均值;
样本均值的方差是总体方差除以N
样本方差为S的平方,样本方差的均值等于总体的方差
区分样本均值的方差与样本方差
还需要区分的是,样本均值与样本,即X拔与X,X与μ,X拔与μ
另外,对于样本方差的方差,考虑构建卡方分布
即样本方差为N-1,除以总体方差后,可以转为N-1的卡方分布,然后样本方差的方差,可以转化为卡方分布的方差,卡方分布的方差为二倍的自由度

两种方法,一种是转为自由度为1的卡方分布,然后注意卡方分布的方差为2^N,均值为N;一种是利用方差的定义,即样本减去均值的差的均值,满足这个式子,所以就是在问样本方差,为原样本方差除以取样数量
还有一种思路是,涉及均值,绝对值等要素组合在一起时,考虑直接积分,利用正态分布的对称性进行求解。

ES^2=DX,E(X拔^2)=D(X拔)+E(X拔)^2,
D(X拔)=1/nDX,E(X拔)=EX

常见分布
正态分布公式背写,


常见分布缩写,P是泊松,E是指数,G是几何分布
常见分布的期望与方差,泊松的期望就是朗姆达,方差?
指数的期望是1/朗姆达,方差为1/朗姆达的平方。(理解为,指数分布的含义为等待时间,参数朗姆达的含义为发生次数,即频率,所以平均等待时间为频率事件间的间隔,1/朗姆达)
几何分布?在指数分布的基础上,就只是方差还要再多乘一个1-p,即1-参数
二项分布为期望为np,方差为np(1-p)

![]()
对于后一项的处理方式,为直接积分,即回归期望的定义。
对于期望式中难以处理的部分,如绝对值以及其他不能转换的部分,可以考虑直接通过期望定义来进行积分计算

第一空,就是直接离散化计算概率,不用考虑卷积公式。第二问就是直接展开,利用独立分布时,EXY=EXEY进行计算

此题需要注意,平均就诊时间是参数的倒数,参数的含义 是一定时间内事件发生的次数、频率,所以间隔时间是参数的倒数
密度:朗姆达E^-朗姆达,分布:1-E^-朗姆达

总点击次数为4,类似前题,直接离散化穷举计算即可
两个都服从泊松分布,第一个参数为3,第二个参数为2。用卷积公式,这两个是独立的,然后有一个联合密度函数,就在那个联合密度函数上进行卷积公式。也不用卷积公式,直接离散化的穷举计算即可

满足指数分布,可以直到各自的均值与方差,然后由相关系数知道均方差,均方差=EXY-EXEY,就求出EXY
指数分布的均值为参数的倒数,方差为参数倒数的平方,也是均值的平方
泊松分布的均值为参数,方差也为参数
几何分布的均值为参数的倒数,方差为参数倒数的平方基础上再乘个Q

基于标准正态分布间的转化
卡方分布是直接相加
T分布是分子为一个标准正态,卡方为分布除以其自由度后开根号 。T的自由度就是分母卡方的自由度
F分布分子分母均为卡方除以其自由度后开根号
样本方差除以方差可以转化为卡方分布
从而,样本方差在分子上时,可为卡方分布;在分母上是,为标准差的形式,则为除以自由度后开根号,即T分布。分子分母都有样本方差,考虑F分布
即出现样本方差,就需要考虑到卡方分布,T分布,F分布

X与Y独立,且都为标准正态分布,那么平方加和为自由度为2的卡方分布,找分位点即可
相同原理可以应用于炮弹落点为(X,Y),且X,Y独立满足标准正态分布,那么落地到原点的距离Z满足Z^2=X^2+Y^2,即Z^2服从自由度为2的卡方分布

第一空直接运算,就是自由度为6的卡方分布

DS^2,考虑构造卡方分布,(N-1)S^2/方差为自由度为N-1的卡方分布,然后卡方分布的方差为两倍的自由度,即可得;第二空,为自由度为N-1的T分布,T分布的均值为0,方差为N/N-2;第三空为自由度为1的卡方分布
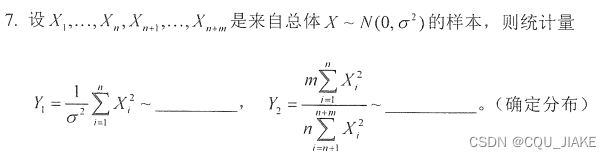
第一空为自由度为N的卡方分布;第二空为F分布,分子自由度为N,分母为M
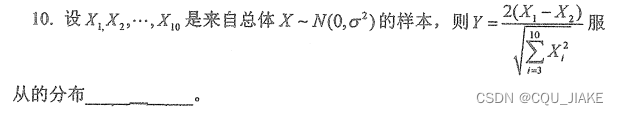
注意分母的i是从3开始1,而不是从1开始的,还有就是T分布与F分布一定要注意除以各自的自由度

注意第一个空,为样本均值,减完后,其分布满足均值为0,因为样本均值的均值等于总体均值
但要注意它的方差,样本均值不是一个常量,而是一个变量,如果为常量,如总体均值,那么这个分布的方差不会变;但是为样本均值,它的方差为总体方差除以n,但是依然不能直接运算,因为X1与样本均值不独立,应把其拆为独立的部分后再进行运算
对于第二问,涉及到样本均值,就一定会有样本方差,考虑自由度减1;不可用第一问的结论,因为这N个分布并不相互独立,而卡方分布必须满足相加的各几个分布相独立
统计量的性质
无偏估计
若为无偏估计,那么统计量的均值为数值期望

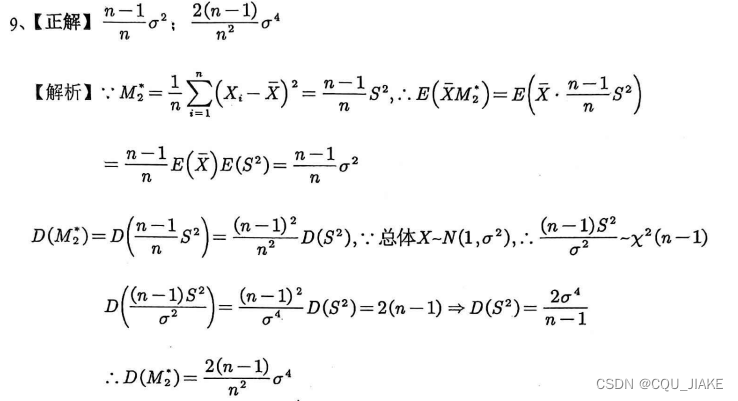


三个想法;第一是直接拆开,然后进行运算;第二是构建辅助分布,然后利用卡方分布;第三同样是辅助分布,但是是利用EX^2转方差的性质。
这里需要注意是可以成功构建一个卡方分布的,因为两两样本间的差值是相互独立的,但是需要注意上例中,涉及到样本均值就无法建立卡方分布,因为样本均值并非与每个样本独立。

置信区间的计算
对于总体均值的置信区间,若总体方差已知,就构建正态分布
若总体方差未知,就构建T分布
对于总体方差的置信区间,无论总体均值是否已知,都构建卡方分布来进行求解,
若总体均值已知,那么分子上的X-均值,就是一个一个算
若总体均值未知,那么分子上的X-均值,就不能一个一个算,因为此时总体均值不知道,那么就是通过样本方差来解决这一问题,即N-1乘以样本方差,等于那个,不过是自由度减一,而且每项减的是样本均值而不是总体均值
在总体方差估计区间中,需注意卡方分布是不对称的,也就是要查两次表,左右都是二分之α的水平

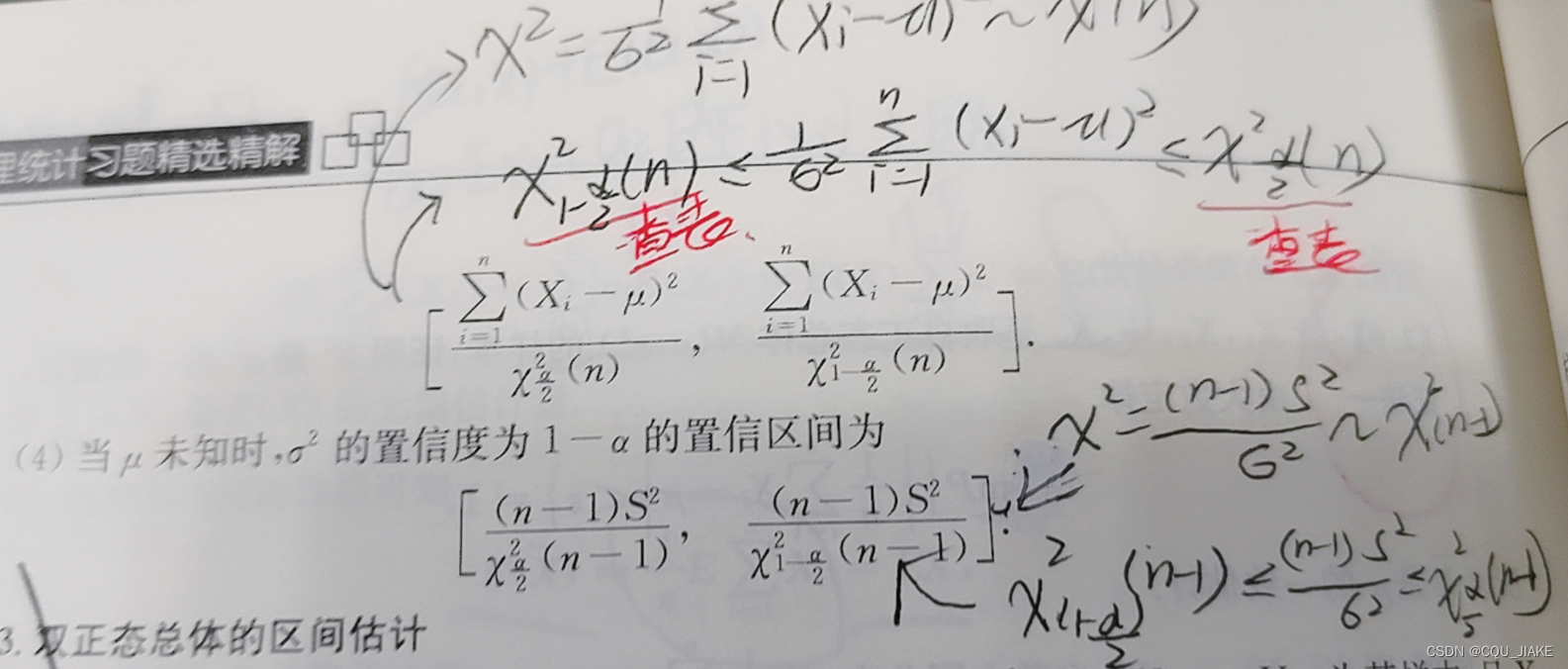

对总体方差估计,总体均值未知,采用N-1的卡方分布,问有无增大,所以检验假设为方差<=70,统计量应分布于左侧,拒绝域为右侧,右侧占0。05

对方差估计,均值未知,考虑自由度为N-1的卡方分布,即(N-1)样本方差除以估计方差,左右两侧为α/2的水平

对总体均值估计,方差已知,采用标准正态,注意假设为均值小于等于32,然后统计量水平为单侧(左侧),拒绝域在右侧

对总体均值的估计,总体方差不知,用自由度-1的T分布,左右为二分之α,即0.025

对总体均值估计,总体方差未知,采用自由度N-1的T分布,置信度95%,分布在左右两侧

对总体方差估计,总体均值未知,采用N-1的卡方分布,分子为N-1*S^2,分母为方差,左右为α/2






问方差,方差估计,那就是卡方分布,由于均值未知,所以依据样本方差构建,样本方差乘(样本数量-1)除以总体方差,就是n-1的卡方分布,问是否明显变化,双侧估计,拒绝域就是比1-α/2小或者比α/2大
第一类第二类错误
第一类第二类错误理解
主要是第二类错误的计算
第一类错误是说原假设为真,然后放弃原假设,即弃真错误;第二类错误是说原假设为假,接受原假设。一般思路为固定犯第一类错误的概率,然后缩小第二类错误的概率。
犯第一类错误的概率就是α,固定后,就可以确定拒绝域边界的情况。
犯第二类错误,原假设为假,依然接受,那么就是依据第一类错误固定下的边界C,可以表达出相应量在的一个区间里(即不在拒绝域内),然后可以计算在实际分布条件下分布在这个区间里的概率
就是说,拒绝域的边界值,和第一类错误的概率,α水平息息相关,互为决定。

变量间转换,概率计算题
求积分公式
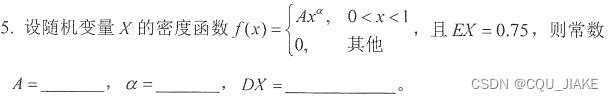
涉及一维与二维
考虑平方的转化
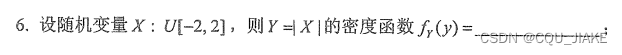

卷积公式计算



证明题

似然估计练练






理解
密度函数与分布函数的理解
有一个函数,它可以取很多值,如果取每个值的概率都一样,那就是分布均匀的,是均匀函数,如果分布不均匀,就不是均匀函数分布;每个值在函数取值出现的概率就是密度函数,均匀时都一样;不均匀时根据出现的值,有其对应的出现概率。
分布函数可以理解为,分布函数这个值,然后函数取值的点落在这个值划定的左区间内的概率(或者可以说是占比)
从这个角度,密度函数的自变量取值范围,就是对应会出现的值,然后这个值通过密度函数会得到其出现的概率;而分布函数就是立一个区间右端点,然后问自变量(可能出现的值)取值在这个区间里的概率。
二维变量密度函数,卷积公式理解
卷积公式就是,原来两个变量x,y,然后有一个z综合了2个变量的信息,通过卷积公式就是把其中一个变量视为常数,然后用z去替换掉剩下的那个变量,利用的方式就是一维的函数替换,求反函数,然后乘一个求导(注意另一个变量在此时表现为常数),之后就得到了把其中一个变量替换后的x,z联合分布(以替换y为例),然后再对每个z收缩其所有的x,即可求得z的单独密度函数。
即替掉哪个变量(计为Y)时,就求Y与Z的关系式(Y为因变量),把X视为常数,然后在函数里踢掉Y为Z,然后乘一个YZ关系式中对Z求导的结果(可能涉及到X,求导时其视为常数),最后就收缩所有的X得到Z的式子。
第一步是要得到联合密度函数,就是把不同变量X,Y的取值综合在一起的一个密度联式
在一维当中,Y与X满足一个关系式(Y为因变量),X已知分布函数,那么转换求反函数,得到X为因变量的与Y的关系式,然后这个表达式对Y求导,取绝对值,把X当中的换掉为Y,就是Y的分布函数
对于泊松分布与指数分布的区分
泊松分布与指数分布共用一个参数,就是朗姆达,这个参数的含义就是一定时间内事件发生的次数,频率,是次数、频率。
相应的,等待时间,寿命,就是频率的倒数。
要根据实际意义确定真正的朗姆达