目录
一、利用真值表求主析取范式、主合取范式
1.例题
二、推理证明
1.推理规则
2.例题
三、符号化命题
四、有穷集的计数
1.包含互斥原理
2.例题
1.文氏图法
2.包含互斥原理法
五、关系的闭包
1.三种闭包
2.Warshall算法
3.例题
六、等价关系
1.定义
2.例题
七、最小生成树的应用题
一、利用真值表求主析取范式、主合取范式
用真值表求出公式的成真赋值和成假赋值,主析取范式:成真赋值用m一一析取组合;主合取范式:成假赋值用M一一合取组合
1.例题

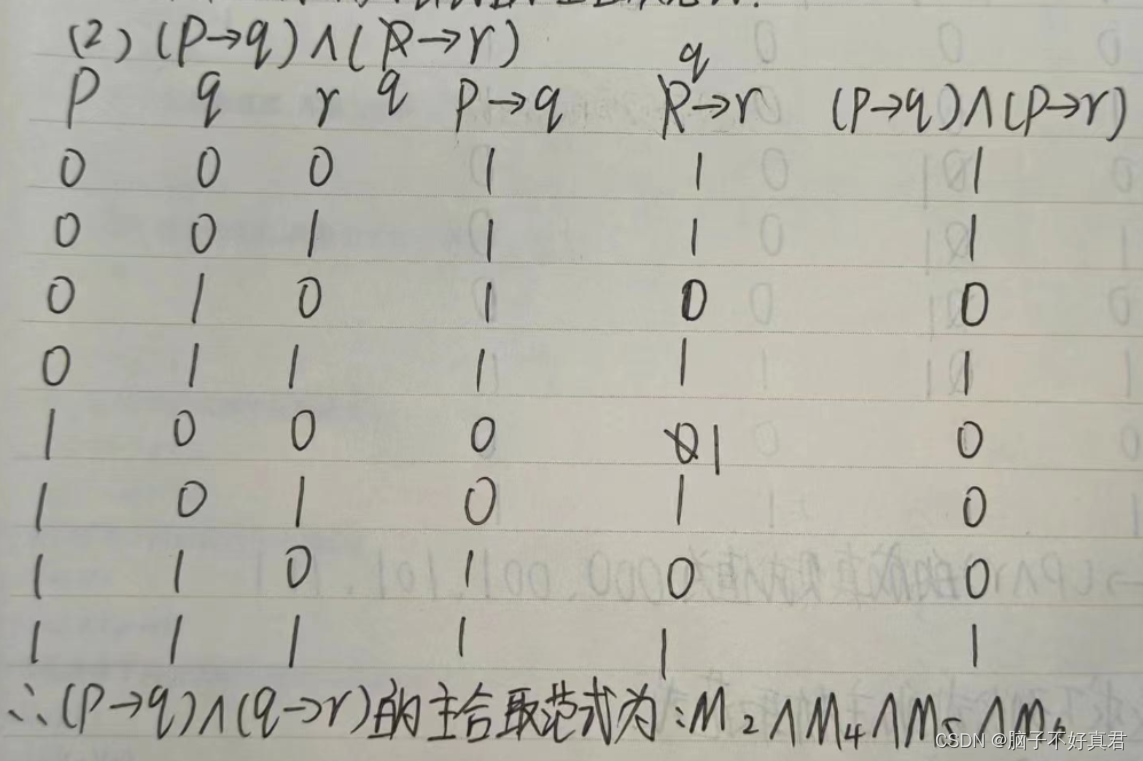
二、推理证明
1.推理规则

2.例题







三、符号化命题




四、有穷集的计数
1.包含互斥原理

2.例题
 1.文氏图法
1.文氏图法
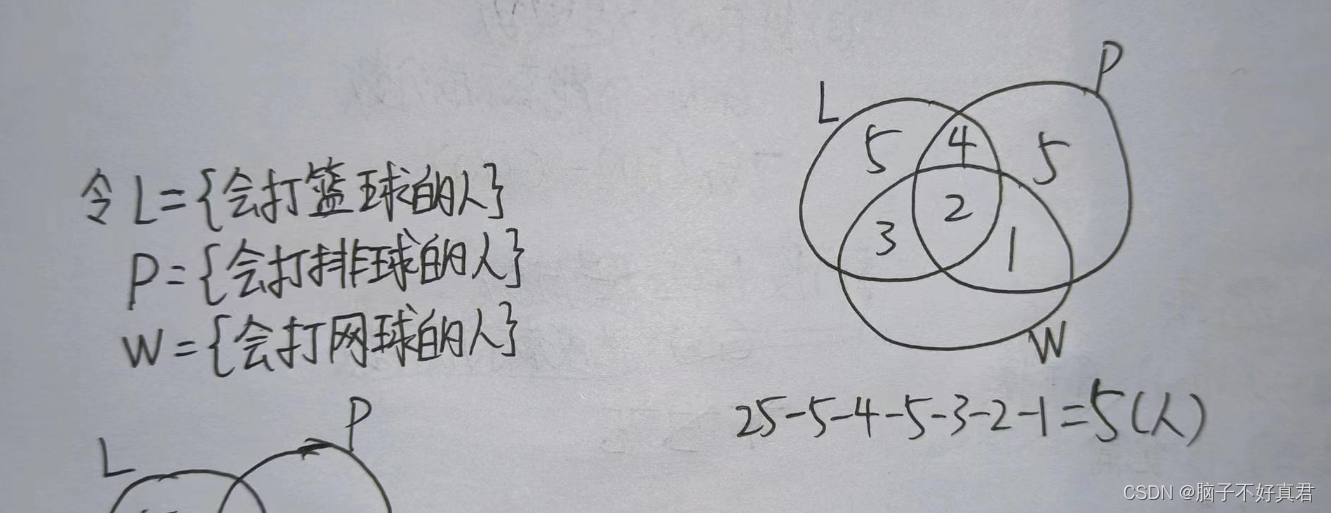
2.包含互斥原理法




五、关系的闭包
1.三种闭包
如果R = {1,2,3},那么R的恒等关系 = {<1,1><2,2><3,3>}
如果R = {<2,3><4,1><6,7>},那么R^-1 = {<3,2><1,4><7,6>}


2.Warshall算法
设M(R的关系矩阵)
当i=1时,看第1列为1的元素所在的行,将第一行加到这些行。
当i=2时,看第2列为1的元素所在的行,将第二行加到这些行。
当i=3时,看第3列为1的元素所在的行,将第三行加到这些行。
当i=4时,看第4列为1的元素所在的行,将第四行加到这些行。
上述加为逻辑加,如下,可以用真(1)假(0)析取来理解:
0+0=0, 0∨0=0
0+1=1, 0∨1=1
1+0=1, 1∨0=1
1+1=1, 1∨1=1
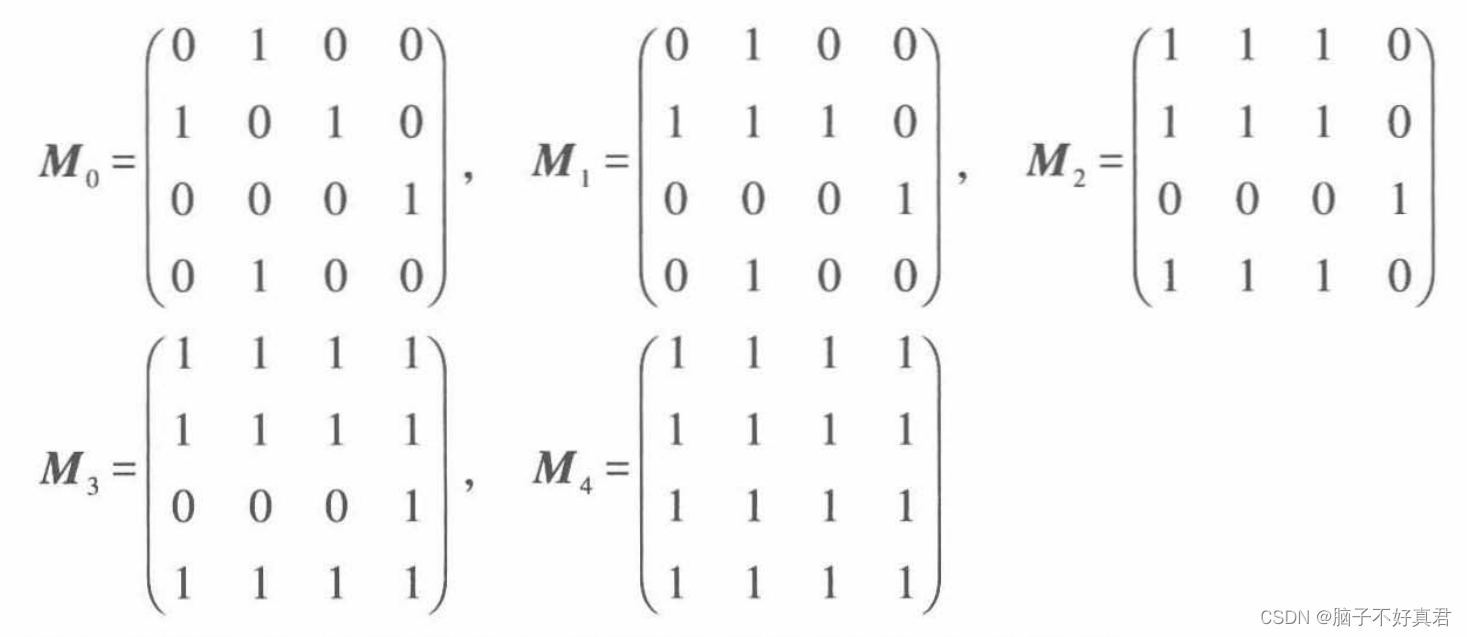
3.例题


六、等价关系
1.定义

也就是说,R在A上满足自反性、对称性、传递性。
2.例题
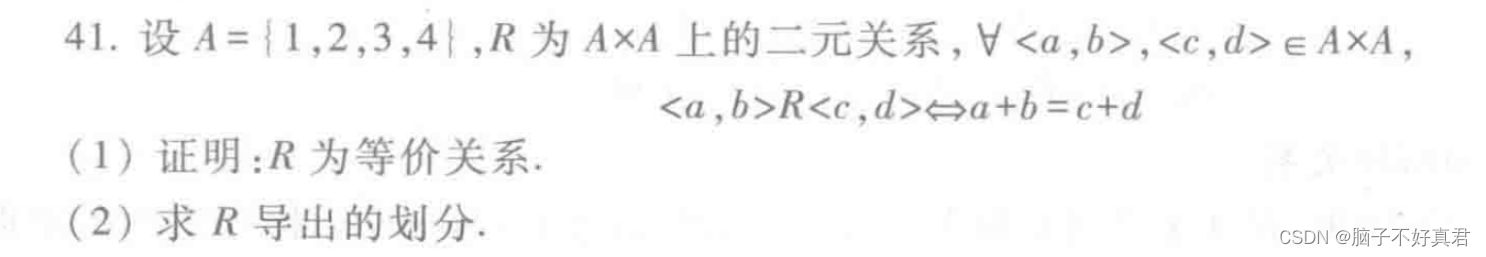

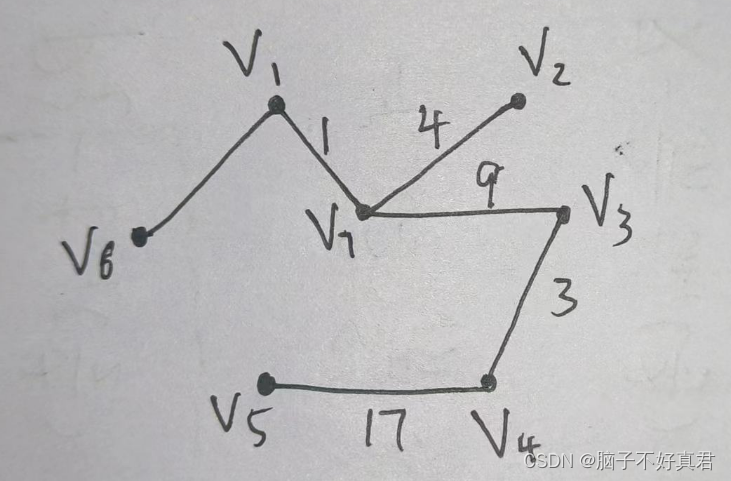
七、最小生成树的应用题
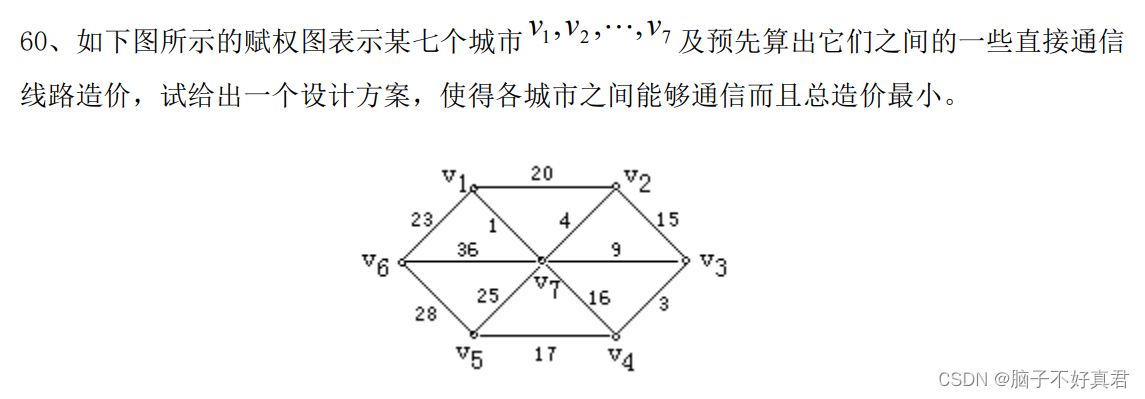
最小生成树画法:每次取权值最小的边,并且不构成回路,直到画出所有顶点。