蓝桥杯 1223 第 2 场小白入门赛

蓝桥小课堂-平方和

模拟 $1^2+2^2+3^2+\cdots+n^2=\dfrac{n\;\cdot\;(n +1)\;\cdot\;(2n+1)}{6}$ 。

 write(n * (n + 1) * (n * 2 + 1) / 6);

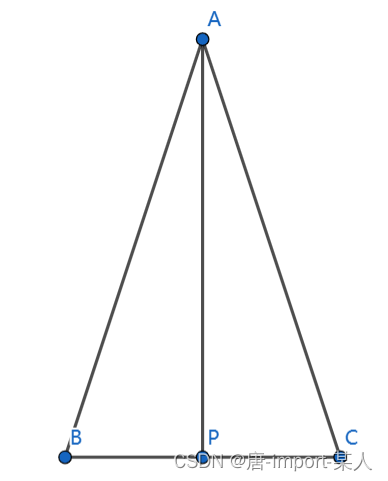
房顶漏水啦

$ma x (最大的行 - 最小的行, 最大的列 - 最小的列) + 1$

ps: $2\le n \le10^{10}$

signed main() {int T = 1;
//    T = read();while (T--) {int n = read(), m = read();int col1 = 1e12, col2 = -1e12, row1 = 1e12, row2 = -1e12;while (m--) {int u = read(), v = read();col1 = min(col1, u), col2 = max(col2, u);row1 = min(row1, v), row2 = max(row2, v);}write(max(col2 - col1 + 1, row2 - row1 + 1));}return 0;
}

质数王国

思路：对每一个数找到其左右两个素数，最小操作次数就是较小差值。
欧拉筛筛出 $1\;,\;10^5+10]$ （范围大于 $10^5$ 你不能保证右边的素数不超过 $10^5$ ）的质数装入 $se t$ 。
二分找较小差值。

signed main() {int T = 1;
//    T = read();while (T--) {int n = read();vector<int> a(n + 1);for (int i = 1; i <= n; ++i) a[i] = read();vector<bool> isprime(N, false);vector<int> prime(N);set<int> s;int cnt = 0;for (int i = 2; i <= N; ++i) {if (!isprime[i]) prime[++cnt] = i, s.insert(i);for (int j = 1; j <= cnt && i * prime[j] <= N; ++j) {isprime[i * prime[j]] = 1;if (!(i % prime[j])) break;}}int ans = 0;for (int i = 1; i <= n; ++i) {if (s.count(a[i])) continue;auto it = s.lower_bound(a[i]);int l, r;if (it == s.end()) r = INF;else r = *it;if (it == s.begin()) l = -INF;else l = *prev(it);ans += min(r - a[i], a[i] - l);}write(ans);}return 0;
}

取余

思路：枚举 $b_i$ 。以 $b_i$ 为模一定能将 $A$ 分成 $A\;/\;b_i+1$ 份。
如上图可以清晰的看出答案。只需要取下面与 $[S\;,\;T]$ 重合的区间长度即可。你可以将其分成三部分思考（首，中间，尾）。
对于 $b_i =1$ 的情况，只有当 $S = 0$ 时才有解，此时应该加上 $A$ 。

signed main() {int T = 1;
//    T = read();while (T--) {int a = read(), b = read(), s = read(), t = read();int ans = 0;for (int i = 2; i <= b; ++i) {if (s > i - 1 || a < s) continue;int p = a / i + 1;if (p > 2) {ans += (p - 1) * (min(t, i - 1) - s + 1) - (s == 0);int cnt = a - (i - 1) - (p - 2) * i;if (cnt - 1 >= s) ans += min(t, cnt - 1) - s + 1;}else if (p == 2) {ans += min(t, i - 1) - s + 1 - (s == 0);int cnt = a - (i - 1);if (cnt - 1 >= s) ans += min(t, cnt - 1) - s + 1;}else ans += min(t, a) - s + 1 - (s == 0);ans += (s == 0) * a;write(ans);}return 0;
}

数学尖子生

思路：容斥。
不能被 $a$ 整除，但一定能被 $1,2,\cdots,3,a-1$ 整除。所以这个数一定是 $1,2,\cdots,3,a-1$ 最小公倍数的倍数，考虑容斥，用 $1,2,\cdots,3,a-1$ 最小公倍数的倍数的个数 $-$ $1,2,\cdots,3,a-1,a$ 最小公倍数的倍数的个数。

int gcd(int a, int b) {return b? gcd(b, a % b): a;}
int lcm(int a, int b) {return a * b / gcd(a, b);}
signed main() {int T = 1;T = read();vector<int> p(N);int cnt = 0;p[cnt] = 1;while (p[cnt] < 1e16) {++cnt;p[cnt] = lcm(p[cnt - 1], cnt);}while (T--) {int a = read(), n = read();if (a > cnt) puts("0");else writeln(n / p[a - 1] - n / p[a]);}return 0;
}

魔术师

思路：线段树 + 矩阵
举例： $[\;a\;,\;b\;,\;c\;]$
- $opt_1\;a\;b$ ： $\begin{bmatrix}\;a\quad b\quad c\;\end{bmatrix}\times\begin{bmatrix}\;0\quad 1\quad 0\;\\\;1\quad 0\quad 0\;\\\;0\quad 0\quad 1\;\end{bmatrix}$
- $opt_2\;a\;b$ ： $\begin{bmatrix}\;a\quad b\quad c\;\end{bmatrix}\times\begin{bmatrix}\;0\quad 0\quad 0\;\\\;1\quad 1\quad 0\;\\\;0\quad 0\quad 1\;\end{bmatrix}$
- $opt_3\;a\;b$ ： $\begin{bmatrix}\;a\quad b\quad c\;\end{bmatrix}\times\begin{bmatrix}\;2\quad 0\quad 0\;\\\;0\quad 1\quad 0\;\\\;0\quad 0\quad 1\;\end{bmatrix}$

ps：要用懒标记，其实和一般线段树下放懒标记没太大区别，第一次接触可能需要自己体会一下。

#include <bits/stdc++.h>
#define il inline
#define get getchar
#define put putchar
#define is isdigit
#define int long long
#define dfor(i,a,b) for(int i=a;i<=b;++i)
#define dforr(i,a,b) for(int i=a;i>=b;--i)
#define dforn(i,a,b) for(int i=a;i<=b;++i,put(10))
#define mem(a,b) memset(a,b,sizeof(a))
#define memc(a,b) memcpy(a,b,sizeof(a))
#define pr 114514191981
#define gg(a) cout<<a,put(32)
#define INF 0x7fffffff
#define tt(x) cout<<x<<'\n'
#define tf(x) cout << "-> " << x << " <-" << '\n';
#define endl '\n'
#define ls i<<1
#define rs i<<1|1
#define la(r) tr[r].ch[0]
#define ra(r) tr[r].ch[1]
#define lowbit(x) (x&-x)
#define ct cin.tie(nullptr),ios_base::sync_with_stdio(false)
using namespace std;
typedef unsigned int ull;
typedef pair<int, int> pii;
int read(void) {int x=0,f=1;char c=get();while(!is(c)) (f=c==45?-1:1),c=get();while(is(c)) x=(x<<1)+(x<<3)+(c^48),c=get();return x*f;
}
void write(int x) {if (x < 0) x = -x, put(45);if (x > 9) write(x / 10);put((x % 10) ^ 48);
}
#define writeln(a) write(a), put(10)
#define writesp(a) write(a), put(32)
#define writessp(a) put(32), write(a)
const int N = 1e5 + 10, M = 2e5 + 10, SN = 1e3 + 10, mod = 1e8, MOD = 998244353;
int c[N], a[N << 2][3], base[3][3], lazy[N << 2][3][3];
void init(int p[3][3]) {for (int i = 0; i < 3; ++i) {for (int j = 0; j < 3; ++j) p[i][j] = i == j;}
}
void pushup(int i, int a[][3]) {for (int j = 0; j < 3; ++j) a[i][j] = (a[ls][j] + a[rs][j]) % MOD;
}
void pushdown1(int a[3][3], int b[3][3]) {int t[3][3];mem(t, 0);for (int i = 0; i < 3; ++i) {for (int j = 0; j < 3; ++j) {for (int k = 0; k < 3; ++k) t[i][j] = (t[i][j] + a[i][k] * b[k][j]) % MOD;}}for (int i = 0; i < 3; ++i) {for (int j = 0; j < 3; ++j) a[i][j] = t[i][j];}
}
void pushdown2(int a[3], int b[3][3]) {int t[3];mem(t, 0);for (int i = 0; i < 3; ++i) {for (int j = 0; j < 3; ++j) t[i] = (t[i] + a[j] * b[j][i]) % MOD;}for (int i = 0; i < 3; ++i) a[i] = t[i];
}
void build(int i, int l, int r) {init(lazy[i]);if (l == r) { a[i][c[l] - 1] = 1; return ;}int mid = (l + r) >> 1;build(ls, l, mid), build(rs, mid + 1, r);pushup(i, a);
}
void modify(int i, int l, int r, int L, int R) {if (L <= l && r <= R) {pushdown1(lazy[i], base);pushdown2(a[i], base);return ;}pushdown1(lazy[i << 1], lazy[i]), pushdown1(lazy[i << 1 | 1], lazy[i]);pushdown2(a[ls], lazy[i]), pushdown2(a[rs], lazy[i]);init(lazy[i]);int mid = (l + r) >> 1;if (L <= mid) modify(ls, l, mid, L, R);if (R > mid) modify(rs, mid + 1, r, L, R);pushup(i, a);
}
signed main() {int T = 1;
//    T = read();while (T--) {int n = read(), m = read();for (int i = 1; i <= n; ++i) c[i] = read();build(1, 1, n);while (m--) {int l = read(), r = read(), op = read(), cla = read() - 1;init(base);if (op == 3) {base[cla][cla] = 2;}else {int clb = read() - 1;if (op & 1) {base[cla][cla] = base[clb][clb] = 0;base[cla][clb] = base[clb][cla] = 1;}else base[cla][cla] = 0, base[cla][clb] = 1;}modify(1, 1, n, l, r);writesp(a[1][0]), writesp(a[1][1]), writeln(a[1][2]);}}return 0;
}