版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。
这个是C#版本的,这里就只放出代码。VB.Net版本请参看 深度神经网络下的风格迁移模型-CSDN博客
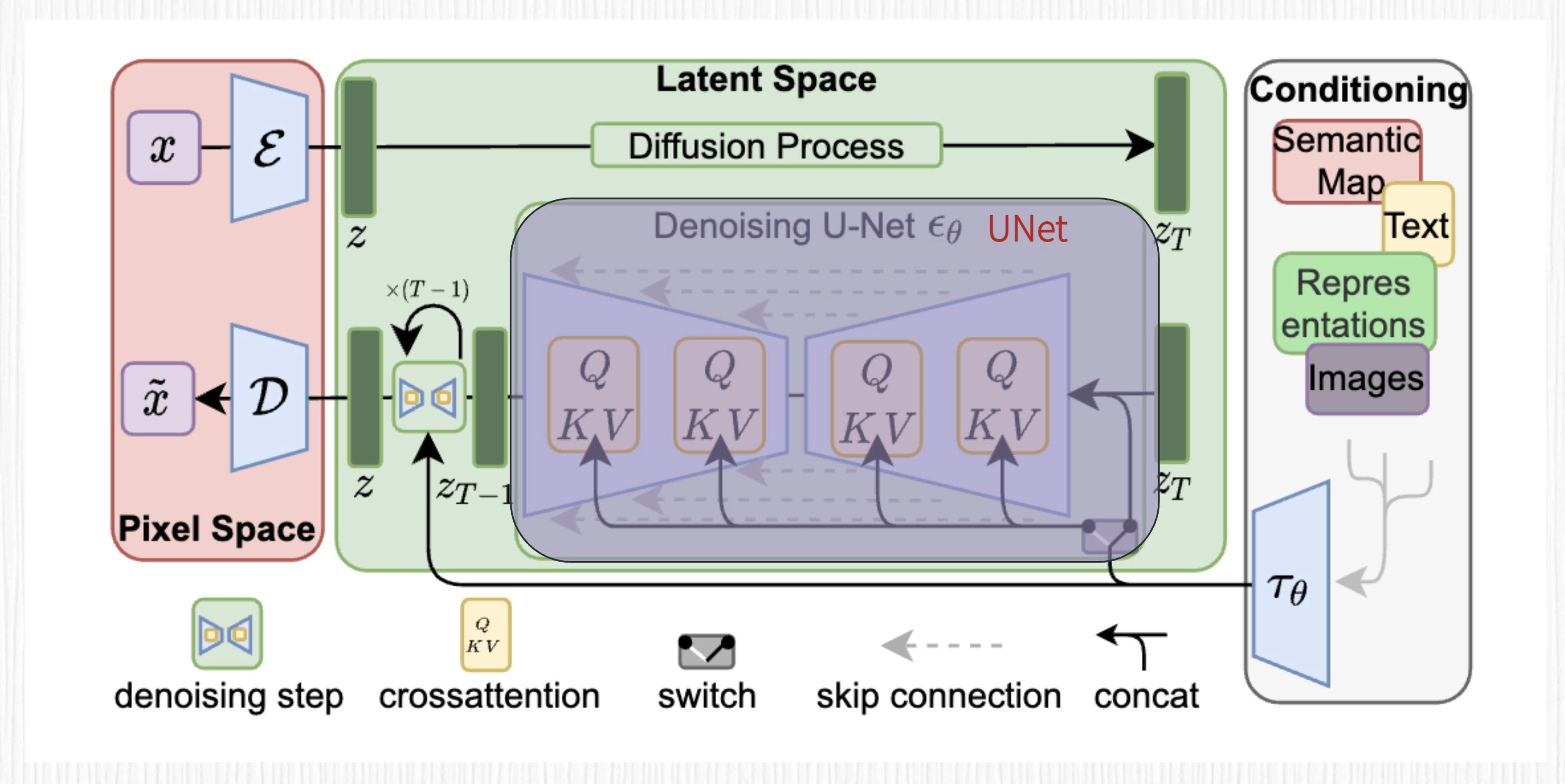
斯坦福大学李飞飞团队的风格迁移模型是一种基于深度学习的图像处理技术,可以将一张图像的风格转移到另一张图像上。该模型最初由Gatys等人提出,后来被李飞飞团队进一步优化和改进。该模型在图像处理领域具有广泛的应用,例如艺术风格转换、视频风格迁移等。
10种模型可以在这里下载:
深度神经网络下的风格迁移模型资源-CSDN文库
原图:

//风格序号int styleindex = 0;//风格迁移private void Button7_Click(object sender, EventArgs e){//需要测试的图像文件Mat m = new Mat("C:\\learnEmgucv\\tower.jpg", ImreadModes.Color);Single hm = m.Height;Single wm = m.Width;//10种风格迁移string[] styles = new string[10];styles[0] = "C:\\learnEmgucv\\styletransfer\\eccv16\\starry_night.t7";styles[1] = "C:\\learnEmgucv\\styletransfer\\eccv16\\composition_vii.t7";styles[2] = "C:\\learnEmgucv\\styletransfer\\eccv16\\la_muse.t7";styles[3] = "C:\\learnEmgucv\\styletransfer\\eccv16\\the_wave.t7";styles[4] = "C:\\learnEmgucv\\styletransfer\\instance_norm\\candy.t7";styles[5] = "C:\\learnEmgucv\\styletransfer\\instance_norm\\feathers.t7";styles[6] = "C:\\learnEmgucv\\styletransfer\\instance_norm\\la_muse.t7";styles[7] = "C:\\learnEmgucv\\styletransfer\\instance_norm\\mosaic.t7";styles[8] = "C:\\learnEmgucv\\styletransfer\\instance_norm\\the_scream.t7";styles[9] = "C:\\learnEmgucv\\styletransfer\\instance_norm\\udnie.t7";'https://blog.csdn.net/uruseibestNet net;net = DnnInvoke.ReadNet(styles[styleindex]);Mat blob ;blob = DnnInvoke.BlobFromImage(m, 1.0, new Size((int)wm, (int)hm), new MCvScalar(0, 0, 0), false, false);net.SetInput(blob);Mat mout = new Mat();mout = net.Forward();//返回一个四维数组Single[,,,] fout;fout = (Single[,,,])mout.GetData();//返回维度://第1维:图像数量,这里是1//第2维:通道数量 //3//第3维:高度 ////第4维:宽度 ////在实际中需要将第2维、第3维、第4维提取出来组成一个图像int channels = fout.GetLength(1);int height = fout.GetLength(2);int width = fout.GetLength(3);VectorOfMat vm = new VectorOfMat();for (int i = 0; i < channels; i++){//取出每个通道Matrix<int> matr = new Matrix<int>(new Size(width, height));for (int j = 0; j < height; j++)for (int k = 0; k < width; k++)matr[j, k] = (int)fout[0, i, j, k];//将每个通道图像加入到VectorOfMat,总共3个通道vm.Push(matr.Mat);}'https://blog.csdn.net/uruseibestMat outputmat = new Mat();//合并通道CvInvoke.Merge(vm, outputmat);ImageBox1.Image = outputmat;if (styleindex == 9)styleindex = 0;elsestyleindex += 1;}处理后的图片:










由于.net平台下C#和vb.NET很相似,本文也可以为C#爱好者提供参考。
学习更多vb.net知识,请参看vb.net 教程 目录