🚀前言

大家好啊！这里阿辉补一下前面操作符遗漏的地方——截断、整型提升和算数转换
看这一篇要先会前面阿辉讲的数据的存储否则可能看不懂
不bb了，铁子们开始今天的学习吧！！！

🚀截断

截断：将数据存储在计算机系统中时，由于存储空间的限制或数据类型的限制，数据可能会被截断或缩减

上面的话什么意思呢？
比如一个int类型的数据有32bit位把它放在char类型类型的变量中，但是char类型仅有8bit位，这时高位将被截断，只保留低位的8bit位
同样地，当一个浮点数超出了系统所能表示的范围时，它的小数部分将被截断，只保留有效数字。在字符和字符串的情况下，如果存储空间不足，则会截断字符串的末尾字符或字符串的一部分

例子👇

char c = 0x01020304;//十进制数
return 0;

打开VS中的内存窗口我们看一下c里面存的是啥

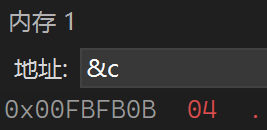
内存窗口是以十六进制形式展示的，c里面仅仅存的是04，发生了截断，前面的十六进制的010203全都截断了

🚀整型提升

C语言中整型算术运算总是至少以缺省整型类型(int)的精度来进行的

缺省就是默认的意思

为了获得这个精度，表达式中的字符和短整型操作数在使用之前被转换为普通整型，这种转换称为整型提升
这是为什么？

因为表达式的整型运算要在CPU的相应运算器件内执行，CPU内整型运算器(ALU)的操作数的字节长度⼀般就是int的字节长度，同时也是CPU的通用寄存器的长度
因此，即使两个char类型的相加，在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度

✈️整型提升是怎样的

对于整型提升分为两种情况：

• 有符号数整型提升高位补符号位
• 无符号数高位直接补0

给铁子们上例子👇

//负数的整形提升
char c1 = -1;
变量c1的⼆进制位(补码)中只有8个⽐特位：
1111111
因为 char 为有符号的 char
所以整形提升的时候，⾼位补充符号位，即为1
提升之后的结果是：
11111111111111111111111111111111
//正数的整形提升
char c2 = 1;
变量c2的⼆进制位(补码)中只有8个⽐特位：
00000001
因为 char 为有符号的 char
所以整形提升的时候，⾼位补充符号位，即为0
提升之后的结果是：
00000000000000000000000000000001
//⽆符号整形提升，⾼位补0

下面这段代码，铁子们知道会输出什么嘛

int main()
{char a = 127;char b = 1;char c = a + b;printf("%d\n", a + b);printf("%d\n", c);return 0;
}

输出结果：

128
-128

为什么呢？

因为a+b计算的时候发生了整型提升
127补码->00000000000000000000000001111111
1  补码->00000000000000000000000000000001
a + b->00000000000000000000000010000000 -> 128
但是把这个值赋给char类型的c时会发生截断
c里面存的就是10000000，由于char在VS中是有符号char
所以在用%d打印c时发生整型提升高位补1
11111111111111111111111110000000 ->补码
10000000000000000000000001111111 
10000000000000000000000010000000 ->原码-> -128

🚀算术转换

如果某个操作符的各个操作数属于不同的类型，那么除非其中一个操作数的转换为另一个操作数的类型，否则操作就无法进行。算数转换是针对字节数大于等于整型的类型来说的。下面的层次体系称为寻常算术转换

  long doubledoublefloatunsigned long intlong intunsigned intint

如果某个操作数的类型在上面这个列表中排名较低，那么首先要转换为另外一个操作数的类型后执行运算。也就是说：算数转换就高不就低，会把低的转换成高的，也就是把字节数小的转换成字节数大的

---

如果觉得文章对你有帮助的话，还请点赞，关注，收藏支持博主，如有不足还请指点，博主及时改正，感谢大家支持！！！