1.原理

决策树（Decision Tree），它是一种以树形数据结构来展示决策规则和分类结果的模型，作为一种归纳学习算法，其重点是将看似无序、杂乱的已知数据，通过某种技术手段将它们转化成可以预测未知数据的树状模型，每一条从根结点（对最终分类结果贡献最大的属性）到叶子结点（最终分类结果）的路径都代表一条决策的规则。

一般，一棵决策树包含一个根节点，若干个内部结点和若干个叶结点。

叶结点对应于决策结果，其他每个结点对应于一个属性测试。每个结点包含的样本集合根据属性测试的结果划分到子结点中，根结点包含样本全集，从根结点到每个叶结点的路径对应了一个判定的测试序列。决策树学习的目的是产生一棵泛化能力强，即处理未见示例强的决策树。

使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。

1.步骤

至于如何生成决策树，具体步骤如下图:

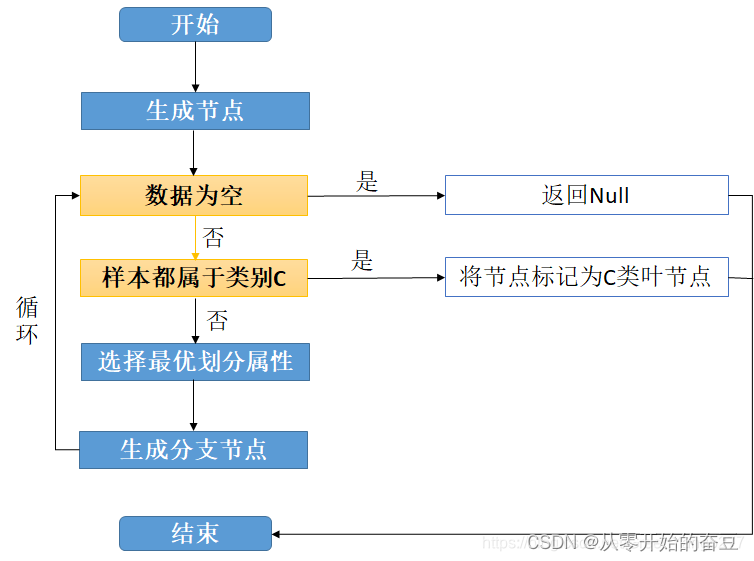
上图就是在生成决策树的过程中经历的步骤。详细步骤如下：

(1).首先从开始位置，将所有数据划分到一个节点，即根节点。

(2).然后经历橙色的两个步骤，橙色的表示判断条件：

若数据为空集，跳出循环。如果该节点是根节点，返回null；如果该节点是中间节点，将该节点标记为训练数据中类别最多的类

若样本都属于同一类，跳出循环，节点标记为该类别；

(3).如果经过橙色标记的判断条件都没有跳出循环，则考虑对该节点进行划分。既然是算法，则不能随意的进行划分，要讲究效率和精度，选择当前条件下的最优属性划分（什么是最优属性，这是决策树的重点，后面会详细解释）

(4).经历上步骤划分后，生成新的节点，然后循环判断条件，不断生成新的分支节点，直到所有节点都跳出循环。

(5).结束。这样便会生成一棵决策树。

2.划分选择

了解了其步骤后，便明白了其关键便是如何寻找最优属性，其选择方法一般有三种。

(1).信息增益

通过方程$$\mathrm{Gain}(D,a)=\mathrm{Ent}(D)-\sum _{v=1}^V\frac{|D^v|}{|D|}\mathrm{Ent}(D^v)$$

来计算每个属性的信息增益，最优属性即为信息增益最大的属性。$$\begin{array}{rl}\mathrm{Ent}(D)& =-\sum _{k=1}^{|\gamma |}{p}_k{\log }_2{p}_k\end{array}$$
，Ent(D)即为样本D的信息熵，由该公式计算可得。

(2).信息增益率

信息增益准则对可取值数目较多的属性有所偏好，增益率定义如下：
$$Gain\_ratio(D,a)=\frac{\mathrm{Gain}(D,a)}{\mathrm{IV}(a)}$$

其中$$\begin{array}{rl}\mathrm{IV}(a)=& -\sum _{v=1}^V\frac{|D^v|}{|D|}{\log }_2\frac{|D^v|}{|D|}\end{array}$$称为属性a的固有值。该划分算法先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的属性。

(3).基尼指数

数据D的纯度可用基尼值来度量，即用如下公式来计算：
$$\mathrm{Gini}(D)=\sum _{k=1}^{|\gamma |}\sum _{k^{\prime }\ne k}{p}_k{p}_{k^{\prime }}=1-\sum _{k=1}^{|\gamma |}{p}_k^2$$

Gini(D)反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率，Gini(D)越小，表示数据集D的纯度越高。而属性a的基尼指数则是根据这个公式推广而得，具体形式如下：$$Gini\_index(D,a)=\sum _{v=1}^V\frac{|D^v|}{|D|}\mathrm{Gini}(D^v)$$
。在候选属性集合A中，选择那个使得划分后基尼指数最小的属性作为最优划分属性。

3.剪枝

剪枝顾名思义就是给决策树 “去掉” 一些判断分支，同时在剩下的树结构下仍然能得到不错的结果。之所以进行剪枝，是为了防止或减少 “过拟合现象” 的发生，是决策树具有更好的泛化能力。

剪枝主要分为两种方法，其一是预剪枝，即在决策树构造时就进行剪枝。在决策树构造过程中，对节点进行评估，如果对其划分并不能再验证集中提高准确性，那么该节点就不要继续王下划分。这时就会把当前节点作为叶节点。其二是后剪枝，即在生成决策树之后再剪枝。通常会从决策树的叶节点开始，逐层向上对每个节点进行评估。如果剪掉该节点，带来的验证集中准确性差别不大或有明显提升，则可以对它进行剪枝，用叶子节点来代填该节点。

2.代码

在scikit-learn中，你可以通过设置DecisionTreeClassifier的参数来进行决策树的剪枝，以防止过拟合。以下是一些常用的参数：

max_depth：决策树的最大深度。这可以防止树过于复杂，导致过拟合。

min_samples_split：分割内部节点所需的最少样本数。如果一个节点的样本数少于这个值，那么这个节点就不会被分割。

min_samples_leaf：在叶节点处需要的最小样本数。这可以防止创建样本数过少的叶节点。

max_leaf_nodes：最大叶节点数量。这是另一种控制树大小的方法。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier# 加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建决策树分类器，并设置剪枝参数
clf = DecisionTreeClassifier(max_depth=3, min_samples_split=10, min_samples_leaf=5, max_leaf_nodes=10)# 训练模型
clf.fit(X_train, y_train)# 预测测试集
y_pred = clf.predict(X_test)# 打印预测结果
print(y_pred)