一、求解三阶微分方程

        对于多变量三阶微分方程求解问题，这里介绍一种求解方法。

例题如下：

       

        对于以上方程，给定边界条件，，，，，。求解和的表达式。

二、解题步骤

（1）建立辅助变量h（t表示自变量），令，，，，；

（2）根据等式阶数确定向量个数，将每阶的求导依次写出来，由（1）可知，，，；

（3）在matlab中建立函数，fun=@(t,h)[h(2);h(4)+h(3)-h(2)-h(1);h(4);h(5);h(1)+h(2)-h(3)+h(4)+h(3)-h(2)-h(1)-h(3)-h(4)-h(5)];%%此时就是将每阶的求导表示出来

[t,h]=ode45(fun,[0,5],[0,0,0,0,0]);
%一阶导数
figure(1)
plot(t,h(:,2),t,h(:,4));
%二阶导数
figure(2)
plot(t,h(4)+h(3)-h(2)-h(1),t,h(:,5))；

（4）对x1和x2进行求解，画图如下，此方法可以有效得到解的图。

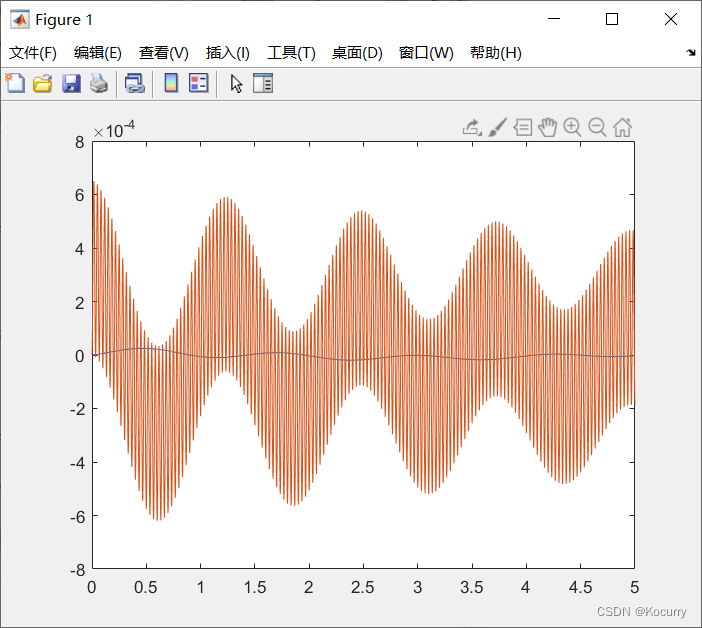
x1

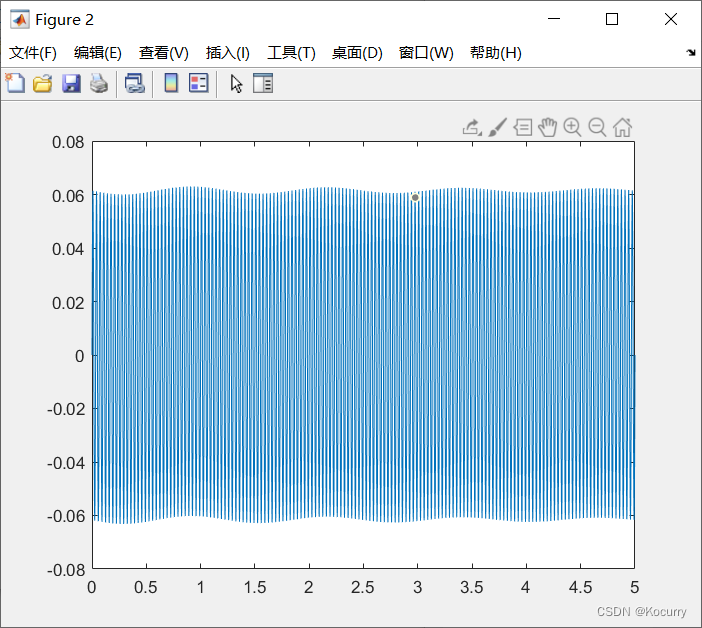
x2