目录
1 电子和程序里的与门,非门,或门,与非门 ,或非门,异或门
1.1 基础电路
1.2 所有的电路情况
1.3 电路的符号
1.4 各种电路对应的实际电路图
2 各种具体的电路
2.1 与门(and gate)
2.1.1 定义:A&B / A and B
2.1.2 and gate的写法
2.1.3 逻辑展开
2.1.4 电路图形
2.1.5 python 里代码
2.2 或门 (or gate)
2.2.1 定义
2.2.2 写法
2.2.3 逻辑展开
2.2.4 电路图形
2.2.5 python代码
2.3 非门 not gate
2.3.1 定义
2.3.2 写法
2.3.3 逻辑表达式
2.3.4 电路图表示
2.3.5 python代码
2.4 与非门 nand gate (not and gate)
2.4.1 定义
2.4.2 写法
2.4.3 逻辑表达
2.5 同非门
2.5.1 定义
2.5.2 写法
2.5.3 逻辑表达
2.5.4 电路图
2.5.5 python代码
2.6 或非门
2.6.1 定义
2.6.2 写法
2.6.3 逻辑表达
2.6.4 电路图
2.6.5 python实现
2.7 异或门 xor gate ()
2.7.1 定义
2.7.2 写法
2.7.3 逻辑表达
2.7.4 电路图
2.7.5 python实现
2.8 传输门
2.8.1 定义
2.8.2 写法
2.8.3 逻辑表达
2.8.4 电路图
2.8.5 python实现
3 感知机
3.1 感知机的定义
3.2 感知机的基础概念
1 门电路
1.0 二极管基础知识
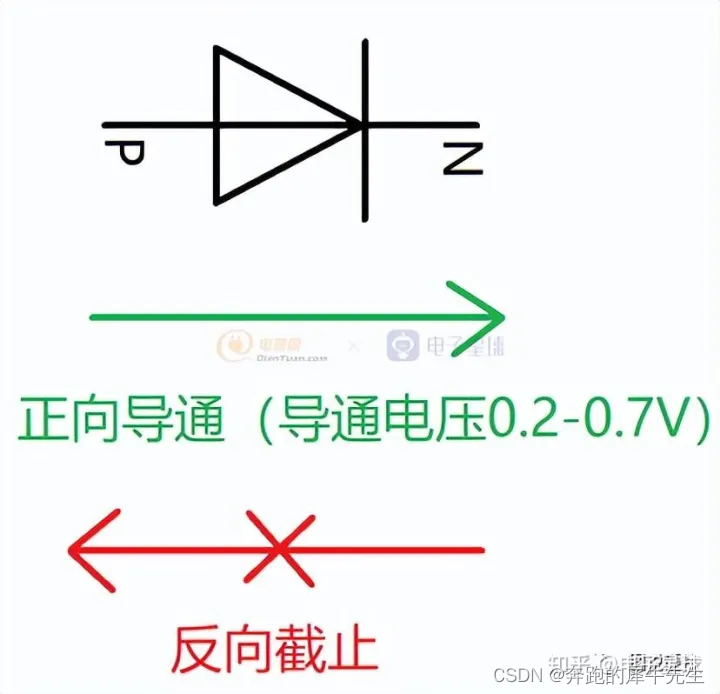
二极管(英语:Diode)
- 是一种电子元件,具有两不对称电导的电极(故名“二极”)。
- 只允许电流由单一方向流过,所以最常应用其整流功能。
1.1 基础电路
- 与门(AND gate)、或门(OR gate)和非门(NOT gate)是数字逻辑电路中的三种基本门电路,它们用于实现不同的逻辑功能。
- 这3种基础电路可以组成其他更复杂的电路
- 与门, and gate, A&B / A and B
- 或门, or gate, A+B / A or B
- 非门, not gate, A- / not A
1.2 所有的电路情况
- 与门, and gate, A&B / A and B
- 或门, or gate, A+B / A or B
- 非门, not gate, A- / not A
- 与非门,not and gate,
- 或非门,not or gate,
- 同或门,
- 异或门,xor
- 传输门
1.3 电路的符号
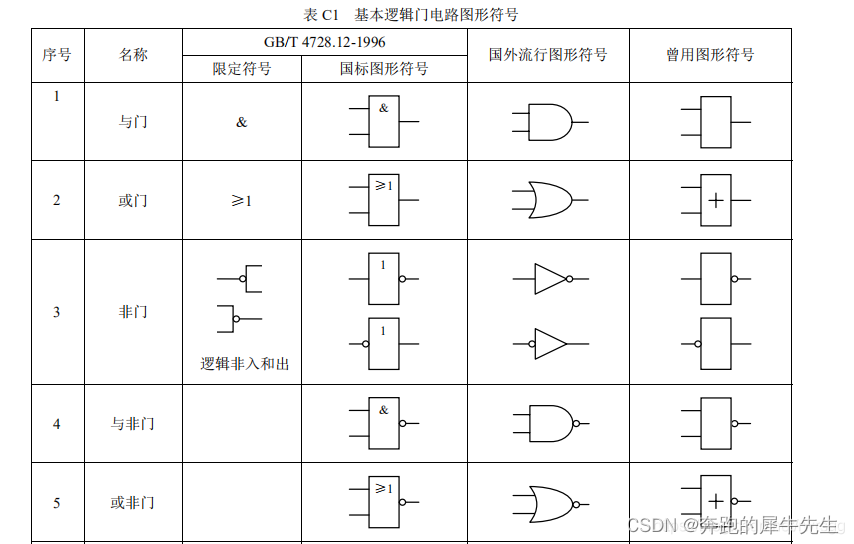
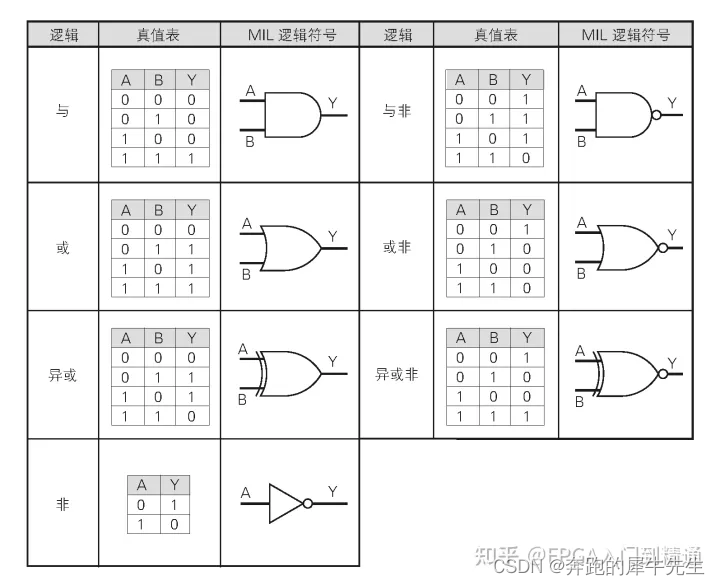

1.4 各种电路对应的实际电路图
2 各种具体的电路
2.1 与门(and gate)
2.1.1 定义:A&B / A and B
- 与门:A&B, A and B
- 与门是一个有两个或更多输入端和一个输出端的逻辑门电路。
- 它的输出信号只有在所有输入信号同时为高(1)时才输出高(1),否则输出低(0)。
- 与门可以用逻辑符号 "∧" 表示。
- 逻辑功能:当且仅当所有输入信号都为高时,输出信号为高。否则,输出信号为低。
2.1.2 and gate的写法
- 与门
- A&B
- A*B
- A and B
2.1.3 逻辑展开
- 1 and 1=1
- 1 and 0=0
- 0 and 1=0
- 0 and 0=0
2.1.4 电路图形
Ua与Ub有一个是低电位(零)输出就是低电位(零),因为电源通过电阻到接地二极管,电压降在电阻上,所以输出就是低电位,只有两二极管都是高电位,输出就是高电位,因为二极管不通,输出就是电源电压了

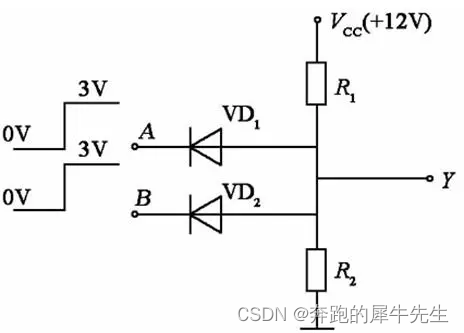
2.1.5 python 里代码
2.2 或门 (or gate)
2.2.1 定义
- 或门(OR gate):或门是一个有两个或更多输入端和一个输出端的逻辑门电路。
- 它的输出信号只要有一个或多个输入信号为高(1),就输出高(1),否则输出低(0)。
- 或门可以用逻辑符号 "∨" 表示。
- 逻辑功能:当至少有一个输入信号为高时,输出信号为高。只有当所有输入信号都为低时,输出信号才为低。
2.2.2 写法
- 或门
- A or B
- A+B
- A|B
2.2.3 逻辑展开
- 1 or 1=1
- 1 or 0=1
- 0 or 1=1
- 0 or 0=0
2.2.4 电路图形
2.2.5 python代码
2.3 非门 not gate
2.3.1 定义
- 非门(NOT gate):
- 非门是一个只有一个输入端和一个输出端的逻辑门电路。
- 它的输出信号是输入信号的逆,即当输入信号为高(1)时,输出为低(0),当输入信号为低(0)时,输出为高(1)。
- 非门可以用逻辑符号 "¬" 或 "!" 表示。
- 逻辑功能:输出信号与输入信号相反。
2.3.2 写法
- 或门
- !A
- not A
2.3.3 逻辑表达式
只有两种情况的分支
- not 0 =1
- not 1 =0
2.3.4 电路图表示
2.3.5 python代码
2.4 与非门 nand gate (not and gate)
2.4.1 定义
2.4.2 写法
- 与非门
- nand gate
- not and gate
2.4.3 逻辑表达
- not (1 and 1) = not 1 = 0
- not (1 and 0) = not 0 = 1
- not (0 and 1) = not 0 = 1
- not (0 and 0) = not 0 = 1
2.5 同非门?
此外还有更为复杂的异或门(XOR, Exclusive-OR),同或门(XNOR, equivalence)。在此就先不展开啦。
2.5.1 定义
2.5.2 写法
2.5.3 逻辑表达
2.5.4 电路图
2.5.5 python代码
2.6 或非门
2.6.1 定义
2.6.2 写法
2.6.3 逻辑表达
2.6.4 电路图
2.6.5 python实现
2.7 异或门 xor gate ()
2.7.1 定义
2.7.2 写法
2.7.3 逻辑表达
2.7.4 电路图
2.7.5 python实现
2.8 传输门
2.8.1 定义
2.8.2 写法
2.8.3 逻辑表达
2.8.4 电路图
2.8.5 python实现
3 感知机
3.1 感知机的定义
3.2 感知机的基础概念
- 阈值
- 感知机
- 只输出一个信号 ,用0,1区别
- 如果输出2个信号,是不是必须神经网络了?