数据流图(DFD)是一种图形化技术,它描绘信息流和数据从输人移动到输出的过程中所经受的变换。
首先给出一个数据流图样例

基本的四种图形

- 直角矩形:代表源点或终点,一般来说,是人,如例图的仓库管理员和采购员
- 圆形(也可以画成圆角矩形):是处理,一般来说,是动作,是动词+名词的形式,处理可以一步一步,再细化,也就是从最顶层,到第1层,到第2层.
- 数据流:是数据的传递,数据的流向,一般来说,是名词,是我们向后传递的那个信息名称.
- 数据存储,可以是一个清单,一个文件,是我们要从中取数据或者存数据的地方.
注意:
当源点和终点相同时,我们要在直角矩形的右下角画一横线.
不断的抽象,但是两头的数据流是不能变的
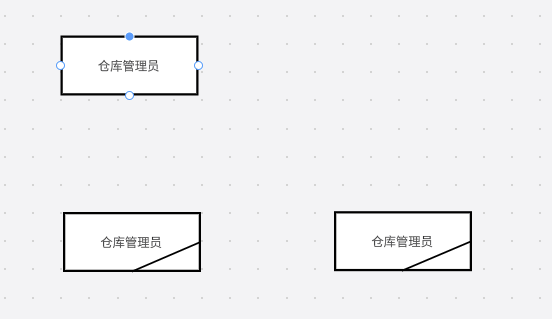
现在可以开画了,注意的是,其实数据流图中,很多描述,同时,我们自己编的,让自己的图更有逻辑,所以,参考答案并不唯一
题目一
银行计算机储蓄系统的工作过程大致如下:储户填写的存款单或取款单由业务员键人系统,如果是存款则系统记录存款人姓名、住址(或电话号码),身份证号码,存款类型、存款日期、到期日期、利率及密码(可选)等信息,并打印出存款存单给储户;如果是取款而且存款时留有密码,则系统首先核对储户密码,若密码正确或存款时未留密码,则系统计算利息并打印出利息清单给储户。
请用数据流图描绘本系统的功能.
首先,画出最顶层数据流图,最顶层数据流图也就是找到源点终点,中间最抽象的一个处理,配上他们之间的数据流即可.
本题中值得注意的是,业务员不是起点.
分析如下:
关键信息是储户存款或取款,若存款,打印存款单给储户,若取款,打印利息清单给储户,中间的抽象就是银行储蓄系统.

其次,将中间的抽象,细分,分为两步,存款和取款.(熟练后这步不需要写)
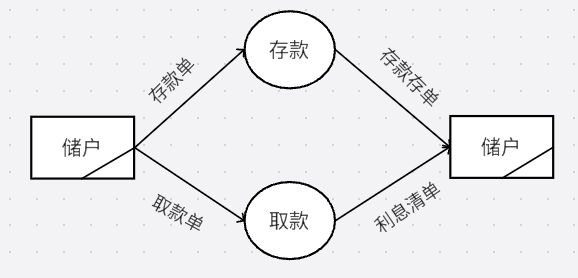
最后,我们再把存款和取款的流程细分.
根据题目信息,存款要先记录信息,打印存款单这两步取款要先核验密码,计算利息,打印利息清单这三步,不要忘记数据存储记录存款信息,取款时读出存款信息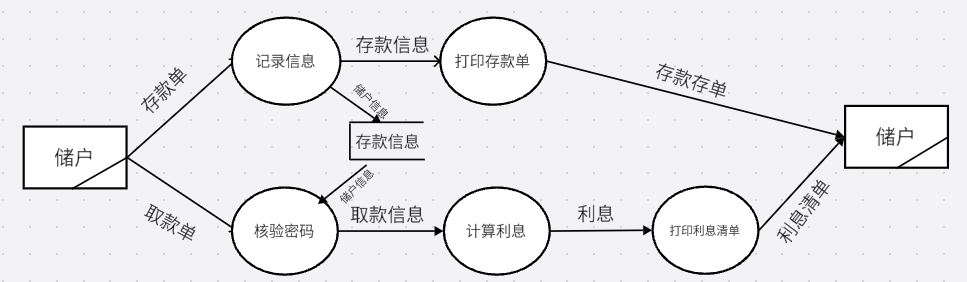
题目二
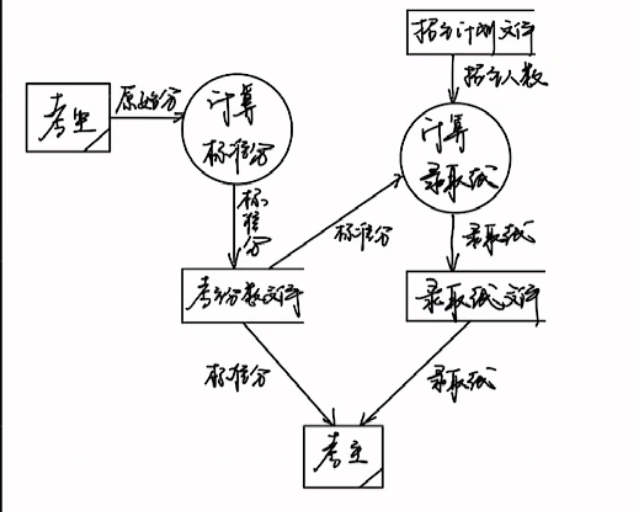
高考录取统分子系统有如下功能
⑴计算标准分:根据考生原始分计算得到标准分,存入考生分数文件
⑵计算录取分数线︰根据标准分、招生计划文件中的招生人数计算录取线,存入录取线文件。
根据要求画出该系统的数据流图。