题目背景：

上述问题的解决方法是使用动态规划来找出两个DNA字符串的最长公共子序列（LCS）。

https://rosalind.info/problems/lcsq/

很经典的动态规划问题了。直接给出解题步骤：

1. 初始化矩阵：创建一个大小为 (len(s) + 1) x (len(t) + 1) 的矩阵。将第一行和第一列的元素初始化为零。这些代表了一个字符串与空字符串的LCS，其长度为零

2. 填充矩阵：对于矩阵中的每个元素 (i, j)（不包括第一行和第一列），检查字符 s[i-1] 和 t[j-1] 是否相等。

• 如果相等，该单元格的值为左上角对角线单元格 (i-1, j-1) 的值加1。
• 如果不相等，取其正上方 (i-1, j) 或左侧 (i, j-1) 单元格中的最大值。

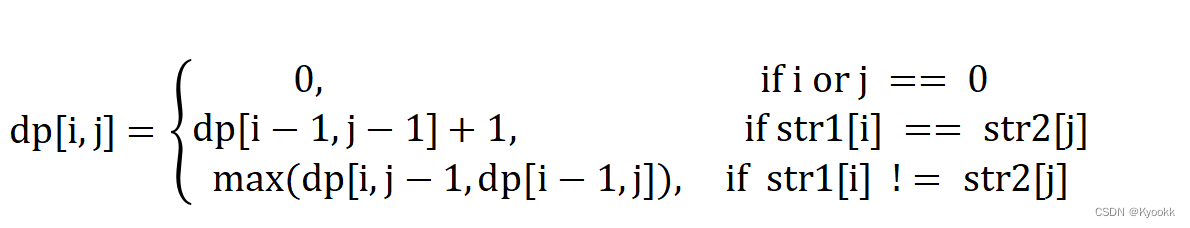
下面上图来解释这个动态的过程：

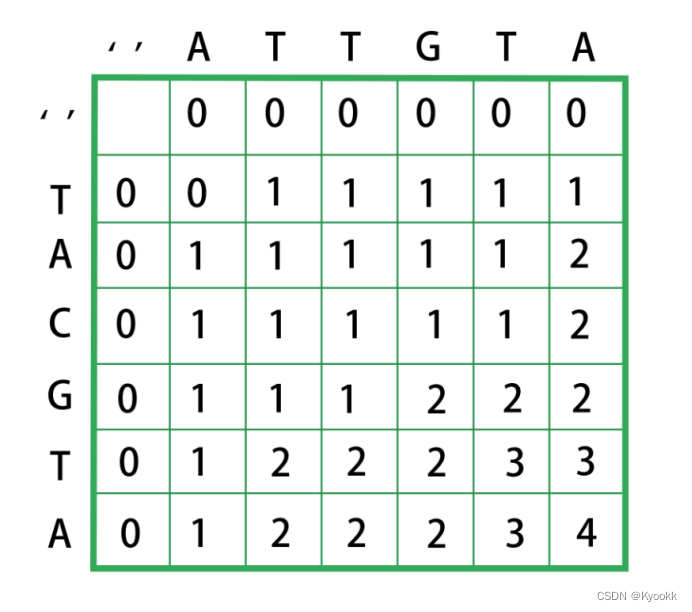
3. 回溯找出LCS：从矩阵的右下角单元格 (len(s), len(t)) 开始回溯以重构LCS。

• 如果 s[i-1] 等于 t[j-1]，则该字符是LCS的一部分。向左上对角线移动，并将此字符添加到LCS中。
• 如果不相等，向值较高的方向移动（向上或向左）。如果两者相等，可以选择任一方向。

4. 重构LCS：在回溯过程中收集的字符（逆序排列）形成了LCS。

题目要求：

给定输入：给定两个最大长度为1kbp的DNA字符串s和t（以FASTA格式表示）。

输出：s和t的一个最长公共子序列。如果存在多个解决方案，你可以返回任何一个。

代码：

from method import fastanamelist,valuelist = fasta("")s = valuelist[0]
t = valuelist[1]def lcs(s, t):# 创建一个动态规划矩阵dp = [[0] * (len(t) + 1) for _ in range(len(s) + 1)]# 填充矩阵for i in range(1, len(s) + 1):for j in range(1, len(t) + 1):if s[i - 1] == t[j - 1]:dp[i][j] = dp[i - 1][j - 1] + 1else:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])# 回溯找出LCSi, j = len(s), len(t)lcs = []while i > 0 and j > 0:if s[i - 1] == t[j - 1]:lcs.append(s[i - 1])i -= 1j -= 1elif dp[i - 1][j] > dp[i][j - 1]:i -= 1else:j -= 1# LCS是逆序构建的return ''.join(reversed(lcs))
print(lcs(s, t))