💗个人主页💗
⭐个人专栏——数据结构学习⭐
💫点击关注🤩一起学习C语言💯💫

导读：

我们在前面学习了单链表，顺序表，栈和队列，小堆，链式二叉树。
今天我们来学习排序，包括直接插入排序，希尔排序，选择排序，堆排序，冒泡排序，快排以及归并排序。
冒泡排序，快排和归并排序我们放在之后分析，今天主要来分析前面的。
关注博主或是订阅专栏，掌握第一消息。

数组打印与交换

为了方便我们来测试每个排序是否完成，我们来写个打印数组和交换两数的函数，方便我们后续的打印与交换。

void PrintArray(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");
}void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}

1. 插入排序

插入排序分为直接插入排序和希尔排序。
基本思想：

把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列。

1.1 直接插入排序

1.1.1 基本思想

直接插入排序是一种简单直观的排序算法，其基本思想是将待排序的元素一个个插入到已排好序的部分中，从而逐步构建已经排序的序列。

1. 首先，将待排序序列的第一个元素视为已排序部分，可以认为该部分只包含一个元素。
2. 然后，依次将后面的元素插入到已排序部分中的正确位置。假设要插入的元素为A，那么从已排序部分的最后一个元素开始向前遍历，如果当前元素大于A，则将当前元素后移一位；反之，找到A应该插入的位置，将其插入到该位置。
3. 重复步骤2，直到所有的元素都被插入到已排序部分中。

直接插入排序的时间复杂度为O(n^2)，其中n为待排序序列的长度。辅助空间复杂度为O(1)，是一种稳定的排序算法。

1.1.2 实现代码

void InsertSort(int* a, int n)
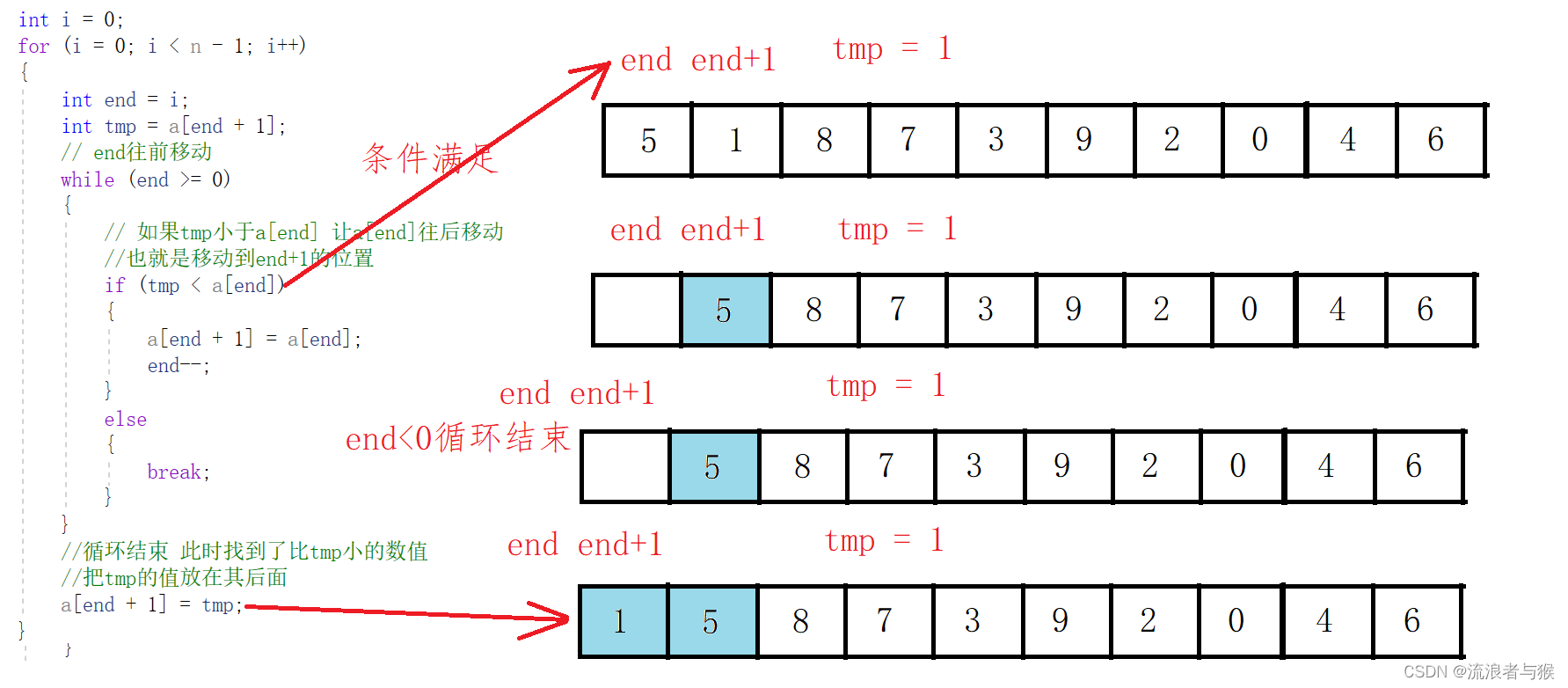
{int i = 0;for (i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];// end往前移动while (end >= 0){// 如果tmp小于a[end] 让a[end]往后移动//也就是移动到end+1的位置if (tmp < a[end]){a[end + 1] = a[end];end--;}else{break;}}//循环结束 此时找到了比tmp小的数值 //把tmp的值放在其后面a[end + 1] = tmp;}
}void TestInsertSort()
{int arr[10] = { 5, 1, 8, 7, 3, 9, 2, 0, 4, 6 };int sz = sizeof(arr) / sizeof(arr[0]);InsertSort(arr, 10);//打印PrintArray(arr, 10);
}
int main()
{TestInsertSort();return 0;
}

1.1.3 图解

1.2 希尔排序

1.2.1 基本思想

希尔排序（Shell Sort）是一种排序算法，也被称为缩小增量排序。
基本思想是将待排序的数组分成若干个子序列，分别进行插入排序，然后逐步缩小增量，直到增量为1时进行最后一次排序。希尔排序的关键在于如何选择增量序列。

1. 初始化增量序列，通常取数组长度的一半作为初始增量，然后每次再缩小增量为前一次的一半。
2. 对每个增量序列进行插入排序，从增量序列的第一个元素开始，将其与对应增量序列的后续元素逐个比较并插入到正确的位置。
3. 缩小增量，重复步骤2，直到增量为1。
4. 最后一次插入排序完成后，数组已经基本有序，但并不是完全有序的，此时再进行一次插入排序，将数组完全排序。

希尔排序的优点是相对于简单插入排序来说，移动的元素较少，比较次数也相对较少，可以提高排序效率。但是希尔排序的时间复杂度依赖于增量序列的选择，不同的增量序列可能会导致不同的排序效果。

1.2.2 实现代码

void ShellSort(int* a, int n)
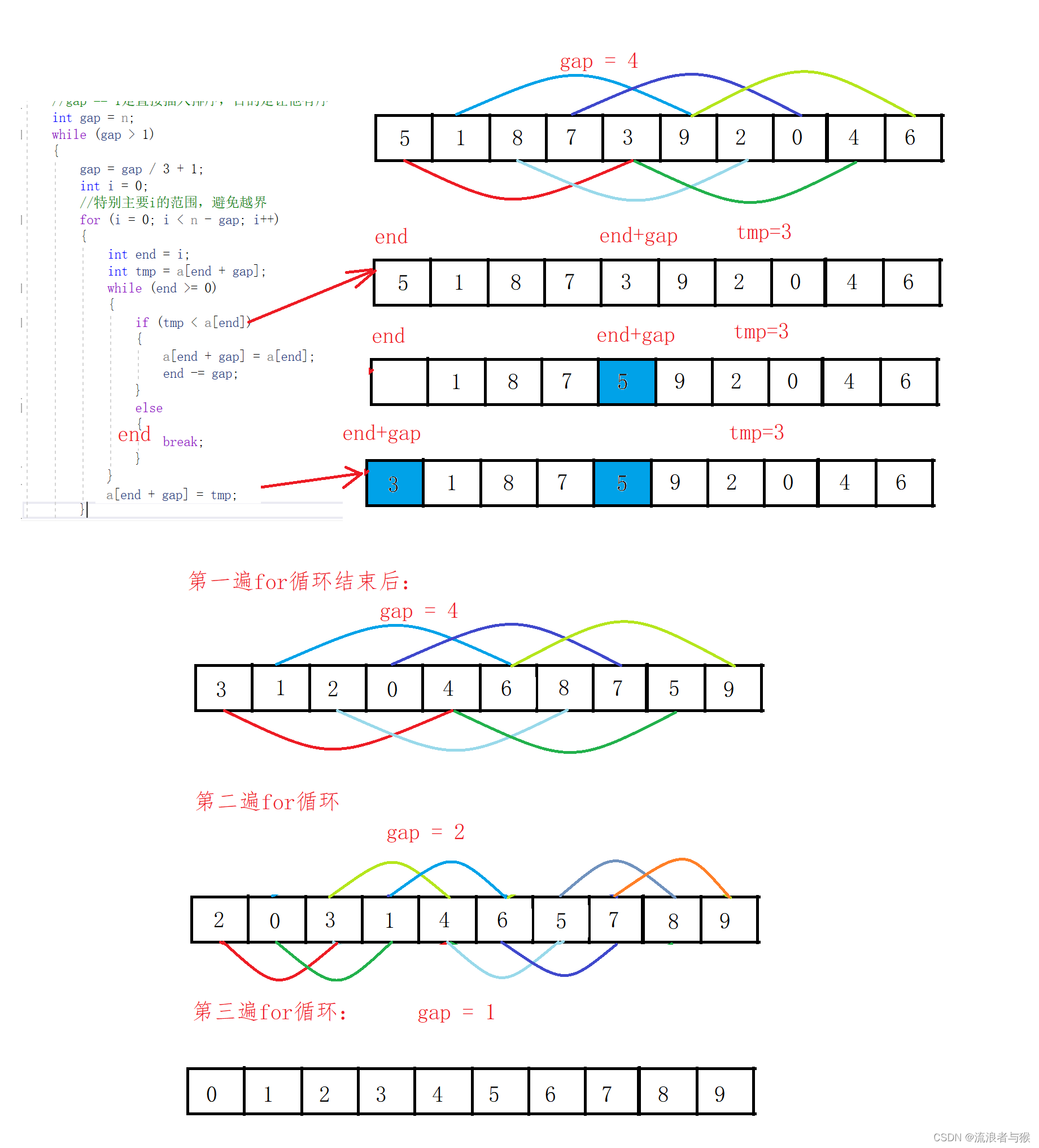
{int gap = n;//gap > 1 时是预排序，目的让他接近有序//gap == 1是直接插入排序，目的是让他有序while (gap > 1){gap = gap / 3 + 1;int i = 0;//特别主要i的范围，避免越界for (i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}void TestShellSort()
{int arr[10] = { 5, 1, 8, 7, 3, 9, 2, 0, 4, 6 };int sz = sizeof(arr) / sizeof(arr[0]);ShellSort(arr, 10);PrintArray(arr, 10);
}int main()
{TestShellSort();return 0;
}

1.2.3 图解

2. 选择排序

选择排序可以分为直接选择排序和堆排序。
基本思想：

每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

2.1 直接选择排序

2.1.1 基本思想

直接选择排序算法的基本思想是找到待排序序列中的最小（或最大）元素，将它与序列的第一个元素交换位置，然后再从剩下的未排序序列中找到最小（或最大）元素，与序列的第二个元素交换位置，依次类推，直到整个序列排好序为止。

1. 遍历待排序序列，假设第一个元素为当前最小（或最大）元素。
2. 从当前元素的下一个位置开始遍历，如果找到比当前元素更小（或更大）的元素，则将其索引记为最小（或最大）元素的索引。
3. 遍历完成后，将最小（或最大）元素与当前元素交换位置。
4. 重复以上步骤，直到整个序列排好序为止。

直接选择排序算法的时间复杂度为O(n^2)，其中n为序列的长度。

2.1.2 实现代码

void SelectSort(int* a, int n)
{int begin = 0;int end = n - 1;while (begin < end){int min = begin;int max = begin;for (int i = begin + 1; i <= end; i++){if (a[i] < a[min]){min = i;}if (a[i] > a[max]){max = i;}}// 把最小的值移到最前面Swap(&a[begin], &a[min]);// 如果max=begin代表第一个元素为最大值// 但是经过上个语句已经把第一个元素和最小的元素交换if (max == begin){max = min;}//最大值放到后面Swap(&a[end], &a[max]);++begin;--end;}
}
void TestSelectSort()
{int arr[10] = { 5, 1, 8, 7, 3, 9, 2, 0, 4, 6 };int sz = sizeof(arr) / sizeof(arr[0]);SelectSort(arr, 10);PrintArray(arr, 10);
}int main()
{TestSelectSort();return 0;
}

2.1.3 图解

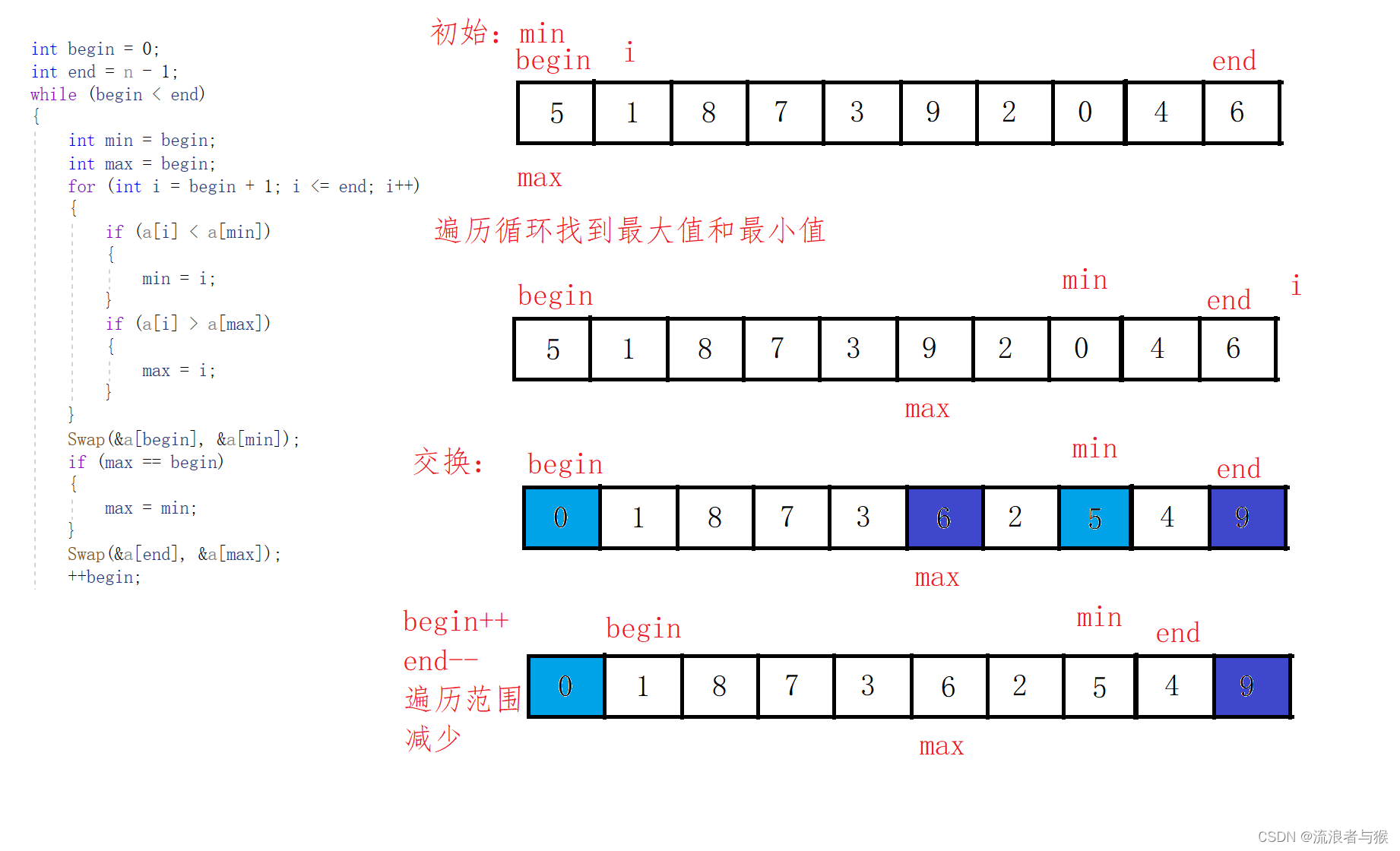
2.2 堆排序

2.2.1 基本思想

堆排序算法的基本思想是利用堆的数据结构进行排序。堆是一种特殊的树状数据结构，分为大顶堆和小顶堆两种类型。
对于大顶堆，父节点的值大于或等于子节点的值；对于小顶堆，父节点的值小于或等于子节点的值。堆排序利用堆的性质，使得每次操作的时间复杂度为O(log n)。

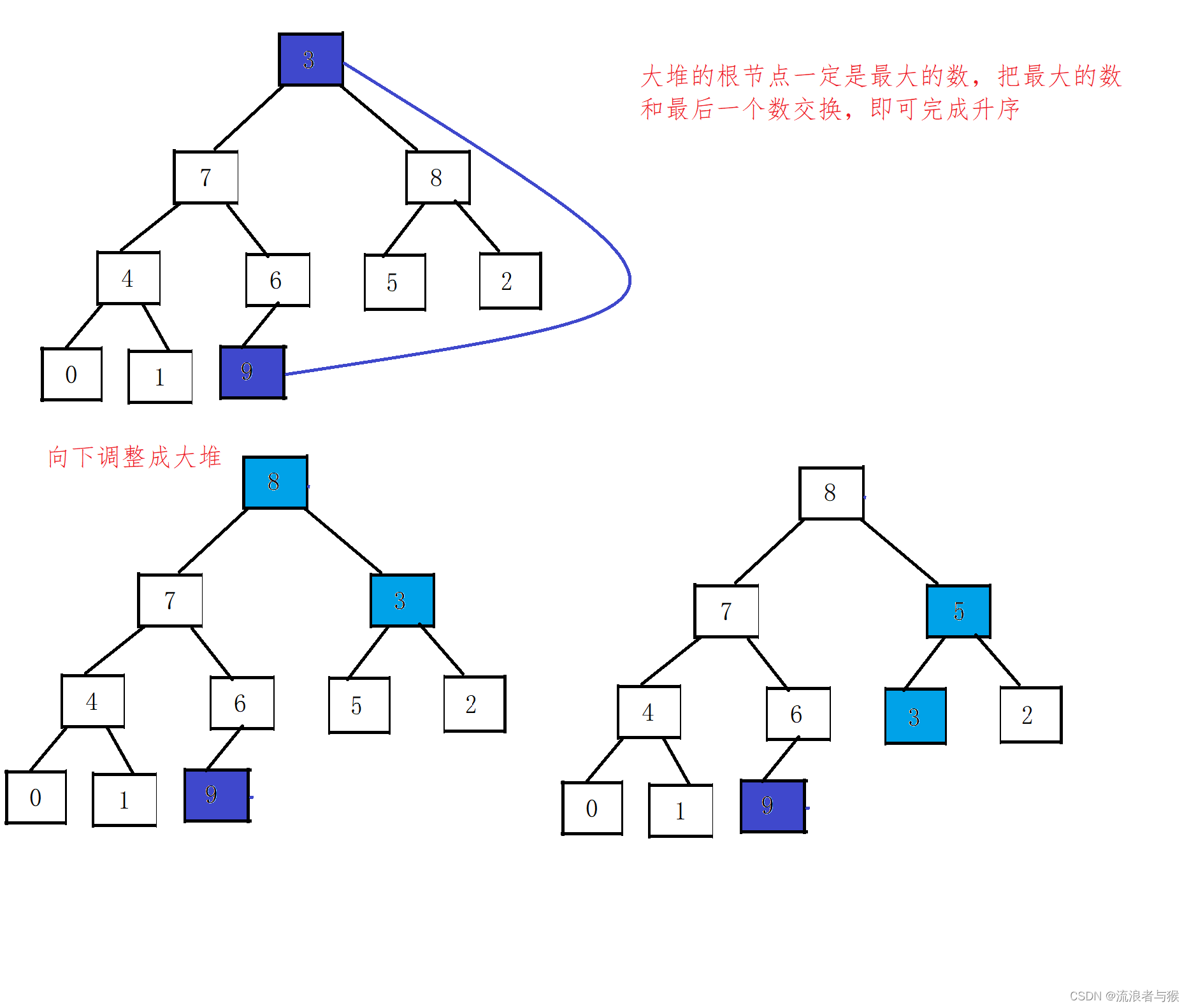
1. 构建初始堆：将待排序序列构建成一个大顶堆。
2. 将堆顶元素（最大值）与堆的最后一个元素交换位置，然后堆的大小减1。这样就将最大值移到了序列的末尾。
3. 对新的堆顶元素进行向下调整（即将堆的根节点调整到正确的位置），使得剩余的元素重新构建成一个大顶堆。
4. 重复步骤2和步骤3，直到堆的大小为1，即完成排序。

主要思想是通过不断地交换堆顶元素和堆的最后一个元素，将最大值依次放到序列的末尾，同时不断地调整堆结构，使得剩余元素保持堆的性质。最后得到的序列就是按照从小到大排序的结果。
堆排序的时间复杂度是O(nlogn)，其中n是序列的大小。堆排序是一种不稳定的排序算法，因为在构建大顶堆的过程中，相同大小的元素可能会交换位置。

2.2.2 实现代码

我们之前有实现过堆，所以我们在这里直接引用即可。

// 向下调整
void AdjustDown(int* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size){// 假设左孩子大，如果解设错了，更新一下if (child + 1 < size && a[child + 1] < a[child]){++child;}// 交换父节点和子节点if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
void HeapSort(int* a, int n)
{//向下调整建大堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}int end = n - 1;// 遍历循环while (end > 0){// 将当前最大元素（堆顶）放到数组末尾Swap(&a[0], &a[end]);// 重新调整剩余元素构建的堆AdjustDown(a, end, 0);--end;}
}
void TestHeapSort()
{int arr[10] = { 5, 1, 8, 7, 3, 9, 2, 0, 4, 6 };int sz = sizeof(arr) / sizeof(arr[0]);HeapSort(arr, sz);PrintArray(arr, 10);
}
int main()
{TestHeapSort();return 0;
}

图解