TwIST算法MALTLAB主程序详解
关于TwIST算法的具体原理可以参考:
链接: https://ieeexplore.ieee.org/abstract/document/4358846
链接: https://blog.csdn.net/jbb0523/article/details/52193209
该算法的MATLAB源代码:
链接: http://www.lx.it.pt/~bioucas/TwIST/TwIST.htm
1. 函数定义与输入输出变量
主函数的定义如下所示,TwIST包含7个输出变量和若干个输入变量,其中包含3个必需输入变量和若干个可选输入变量(varargin)。具体每个变量的含义可以参考MATLAB TwIST.m文件中的解释。下文仅对一些关键参数进行解释。
function [x,x_debias,objective,times,debias_start,mses,max_svd] = ...TwIST(y,A,tau,varargin)
该算法主要解决如下正则化问题:
arg min_x = 0.5*|| y - A x ||_2^2 + tau phi( x )
也就是论文中式(1)所示,注意在MATLAB代码中存在一些符号表示的改变。如K➡A,λ➡tau等。
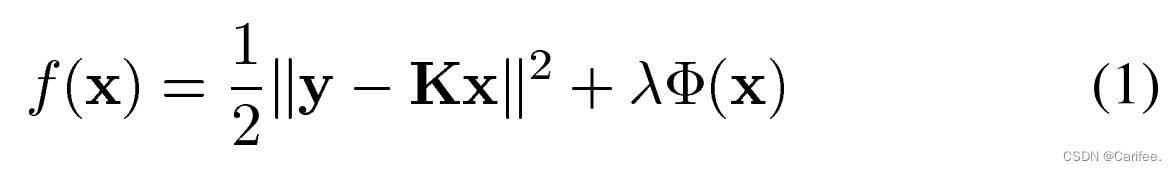
其具体的迭代公式如原论文中式(17)-(19)所示
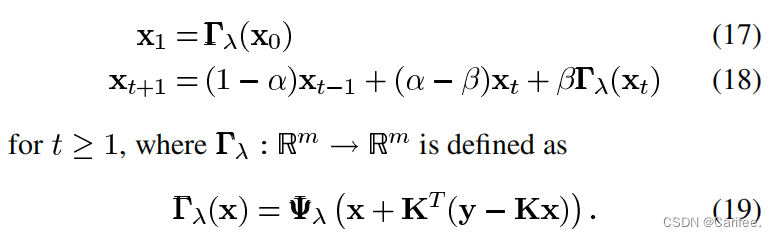
从式(17)-(19)中看,我们需要设置 x 0 , α , β , y , K , Ψ λ x_{0},\alpha,\beta,y,K,\Psi_{\lambda} x0,α,β,y,K,Ψλ等一系列参数,迭代公式方可正确运行。算法的输出变量,x即为目标的估计值,x_debias为目标估计值的去偏结果,获得这一结果往往需要在主循环迭代结束后,通过适当的去偏迭代,消除正则化器造成的一些偏差。
| 输入变量 | 含义 |
|---|---|
| y | 测量结果,可以为一维向量或者二维数组 |
| A | 对应原论文中的K |
| tau | 正则化参数,对应原论文中的λ |
| Psi | 去噪函数句柄,对应原论文中的去噪函数ψ |
| Phi | 正则化器的函数句柄,对应原论文中的Φ |
| lambda | TwIST算法的lam1参数,对应原论文中的 λ 1 \lambda_{1} λ1参数,论文中的 λ N \lambda_{N} λN在程序中被设置为常数1。若 λ 1 = 1 \lambda_{1}=1 λ1=1,TwIST算法等价于IST算法。 |
| alpha | TwIST的alpha参数 (详见论文式 (22)) |
| beta | TwIST的beta参数 (详见论文式 (23)) |
2.算法主要步骤
TwIST.m的代码很长,但主要包含的内容并不多。下文主要对在代码中关键部分进行解释。按照从前往后的顺序,主要包含了以下几个内容:
(1)变量注释。
这一部分对函数的每一个变量都进行了注释,包括必须变量和可选变量。建议按照以上迭代公式了解关键参数的含义。
(2)变量设定。
这一部分主要在变量注释和初始化两部分之间。
主要定义了
- 各个变量的默认值。
- 使用一个switch-case分支语句读取varargin所代表的可选输入参数,实现可选变量的自定义功能。
- 对主要变量,如alpha和beta进行设定。对于这个部分,多说一点。如原论文中所示
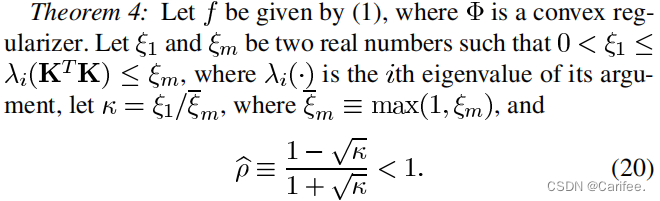

实际上存在如下关系:
0 < ξ 1 ≤ λ 1 < λ N ≤ ξ m , ξ ‾ m ≡ m a x ( 1 , ξ m ) 0< \xi_{1} ≤ \lambda_{1} < \lambda_{N} ≤ \xi_{m} , \overline{\xi}_{m}≡max(1,\xi_{m}) 0<ξ1≤λ1<λN≤ξm,ξm≡max(1,ξm)
而在程序中,作者直接用 λ 1 \lambda_{1} λ1表示了 ξ 1 \xi_{1} ξ1,同时设定 ξ m \xi_{m} ξm为 λ N = 1 \lambda_{N}=1 λN=1。虽然可能有点误差,不过我觉得无可厚非。
关于函数句柄,需要注意的是,这里的x并不是迭代的解x,而是一个指代未知变量的参数。实际上这里的x可以用任何符合矩阵计算条件的参数,如下面的AT(y)中的y。
if ~isa(A, 'function_handle')AT = @(x) A'*x;A = @(x) A*x;
endAty = AT(y);
(3)初始化。
初始化主要实现了 x 0 x_{0} x0的设置方法,验证了phi(x)和psi(x)函数是否有效,以及其他一些变量的初始设置。
(4)TwIST主循环迭代。
这一部分是整个代码中最主要的部分。
TwIST算法的迭代包含两个主要部分:TwIST迭代和IST迭代。IST_iters和TwIST_iters的值用于确定当前应该执行哪一种迭代。根据条件判断,当TwIST_iters达到特定阈值或满足特定条件时,会切换到执行IST迭代,而不是继续TwIST迭代;反之亦然。
这一部分主要包含2个while循环,两个while循环会一直运行,直到满足对应条件。
在第二个while循环中有一个 if-else结构,用于判断进行何种操作。在TwIST循环中,IST_iters和TwIST_iters并不会一直增加,而只是一个判断flag,结合对应的if else,完成判断。迭代次数的增加实际上由iter控制。
建议在主循环设置断点,并将IST_iters和TwIST_iters后边的分号去掉,使用demo进行调试。观察IST_iters和TwIST_iters的值变化。这样,IST_iters和TwIST_iters取什么值执行什么语句就一清二楚了。
去噪函数的作用
此外,在主循环中,还有一行比较重要。它是去噪函数的意义所在。
x = psi_function(xm1 + grad/max_svd,tau/max_svd);
代码中其他位置的psi_function只是传参或者验证,而该位置的psi_function是起到了实质作用的。psi_function主要用于执行阈值或收缩操作,通常涉及对给定向量或信号进行阈值处理。它可能采用软阈值(soft thresholding)或硬阈值(hard thresholding)等技术,用于将信号的幅度调整为零或接近零,从而产生更稀疏的表示。
关于去噪函数的定义,原论文中并没有直接关于 Ψ λ \Psi_{\lambda} Ψλ的明确定义,仅仅在II. B 部分给出了一个形而上的说明。形而下的例子可以参考MATLAB文件夹中hard.m和soft.m,这是两个常用的去噪函数,硬阈值和软阈值。

稀疏性操作
if sparsemask = (x ~= 0);xm1 = xm1.* mask;xm2 = xm2.* mask;end
以上代码是处理稀疏性的操作。当 sparse 变量为真时(即 sparse 变量为非零值),代码会执行以下操作:
- 首先,创建一个逻辑掩码 mask,该掩码用于标识变量 x 中非零元素的位置。也就是说,mask 的元素为 1 表示对应 x 中的元素不为零,为 0 表示对应 x 中的元素为零。
- 然后,通过将 xm1 和 xm2 分别与 mask 相乘,将 xm1 和 xm2 中对应于 x 中零元素位置的部分置为零。
- 这样可以确保在算法的迭代过程中,对 x 的更新仅在非零位置进行,以保持其稀疏性。
(5)去偏。
在主循环之后,还有一个去偏阶段(debias phase)。这是一个可选操作,作者给出的解释是 :
If the ‘Debias’ option is set to 1, we try to remove the bias from the l1 penalty, by applying CG to the least-squares problem obtained by omitting the l1 term and fixing the zero coefficients at zero.
可见,这一部分主要是为了消除l1惩罚的偏差。