前言:
本篇博客主要了解什么是树，什么是二叉树，以及他们的概念和结构。

---

一、树的概念及结构

1.1 树的基本概念

树（Tree）是一种非线性数据结构,是一种层次结构，其中每个节点都有一个父节点（除了根节点）和零个或多个子节点。

树（Tree）这个数据结构被称为“树”，是因为它的图形结构在形状上类似于自然界中的倒立的树。

考虑一棵真实的树，它有一个主干（树干），从树干上生长出许多分支，这些分支又分支出更小的枝叶，最终形成树冠。整体上，树的形状呈分层的结构，从根部到叶子的路径是有序的。

对比到数据结构中的树，树的根节点相当于树的根部，而节点和边的层次结构形成了树状的分支。这种分层结构反映了树的层次性质，每一层都代表了不同的层次或深度。

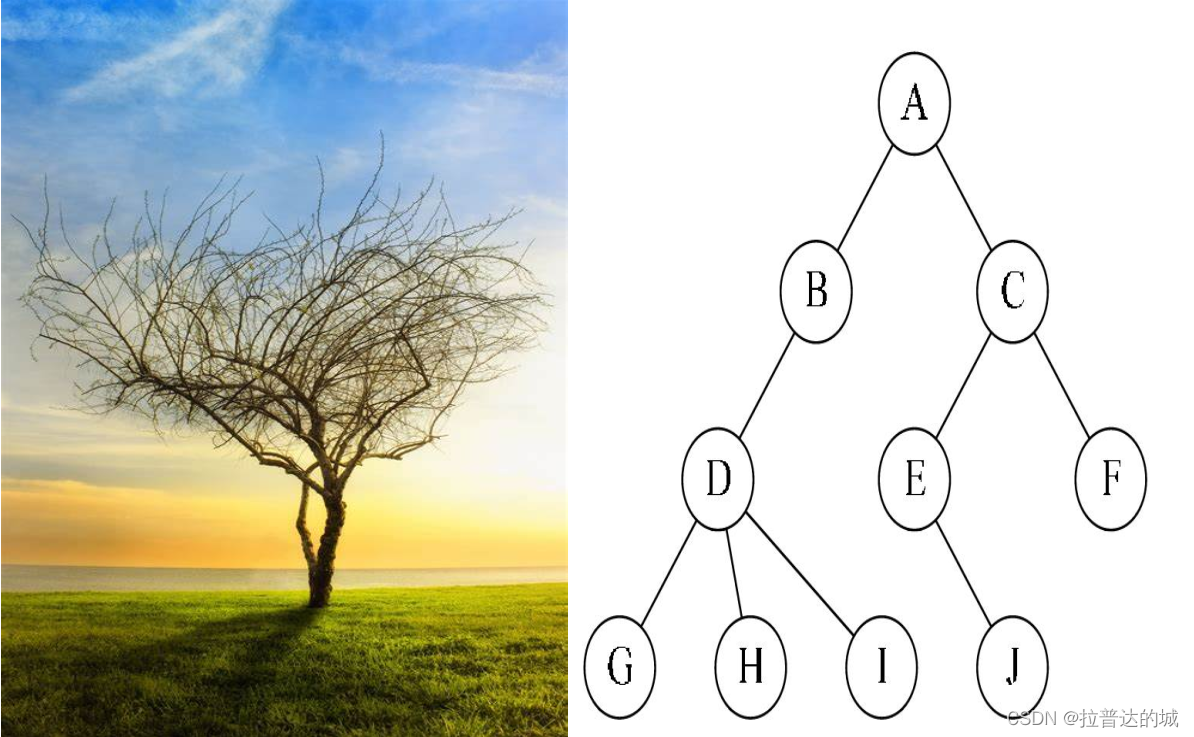
当判断一个数据结构是否是树时，可以考虑以下几个特点：

1. 有且仅有一个根节点： 树结构只有一个根节点，所有的其他节点都通过边连接到根节点。

2. 每个节点有零个或多个子节点： 每个节点可以有零个或多个子节点，这些子节点也是树的节点，形成了树的分支结构。

3. 没有循环： 在树中不能存在环，即不能有从某个节点出发经过若干边回到该节点的路径。

4. 节点之间是有序的： 树中的节点之间是有序的，即每个节点都有一个特定的位置，而子节点的顺序也是确定的。这个顺序通常是由添加或创建节点的顺序来确定的。

5. 任意两节点间有唯一路径： 从树的根节点到任意一个节点，都有唯一的路径。

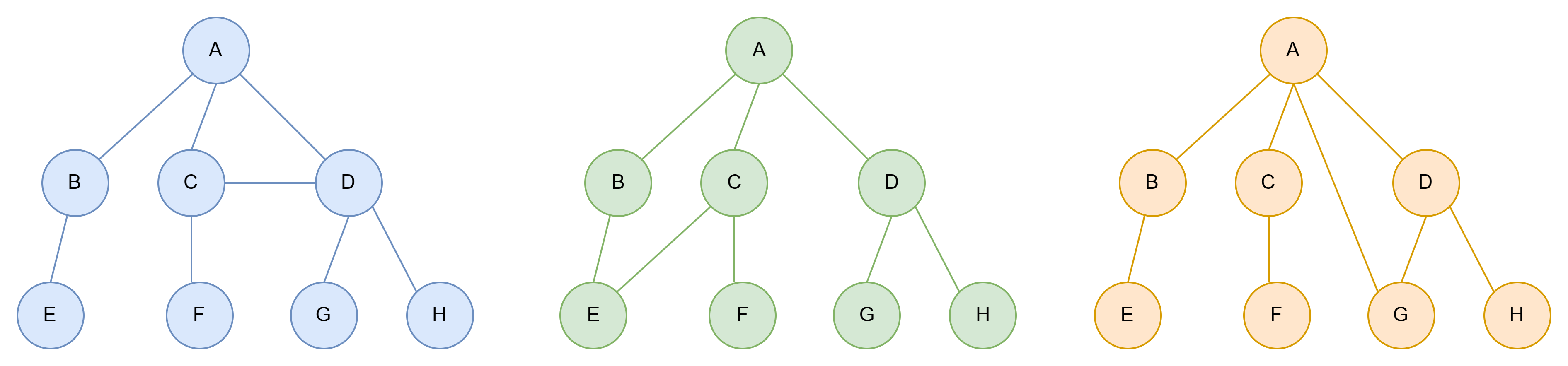
以下是一些非树的例子

---

1.2 树的相关特征

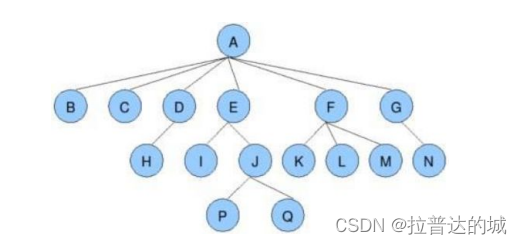
1. 节点的度： 一个节点含有的子树的个数称为该节点的度； 如上图：A的为6
2. 叶节点或终端节点： 度为0的节点称为叶节点； 如上图：B、C、H、I…等节点为叶节点
3. 非终端节点或分支节点： 度不为0的节点； 如上图：D、E、F、G…等节点为分支节点
4. 双亲节点或父节点： 若一个节点含有子节点，则这个节点称为其子节点的父节点； 如上图：A是B的父节点
5. 孩子节点或子节点： 一个节点含有的子树的根节点称为该节点的子节点； 如上图：B是A的孩子节点
6. 兄弟节点： 具有相同父节点的节点互称为兄弟节点； 如上图：B、C是兄弟节点
7. 树的度： 一棵树中，最大的节点的度称为树的度； 如上图：树的度为6
8. 节点的层次： 从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
9. 树的高度或深度： 树中节点的最大层次； 如上图：树的高度为4
10. 堂兄弟节点： 双亲在同一层的节点互为堂兄弟；如上图：H、I互为兄弟节点
11. 节点的祖先： 从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先
12. 子孙： 以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙
13. 森林： 由m（m>0）棵互不相交的树的集合称为森林；

---

1.3 树的实现

树有很多种实现方式如：双亲表示法，孩子表示法、孩子双亲表示法以及孩子兄弟表示法
等。我们这里就简单的了解其中最常用的孩子兄弟表示法。

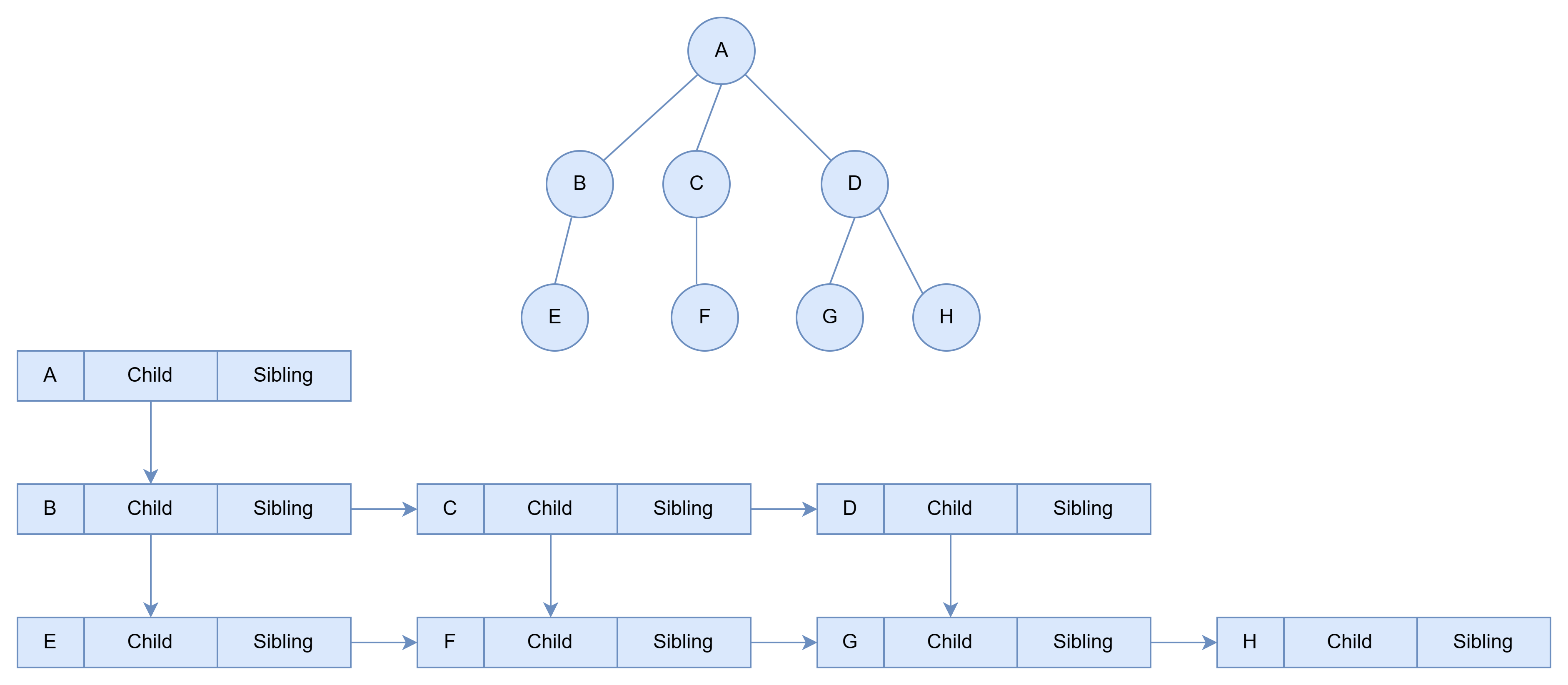
孩子兄弟表示法通常每个节点保存了指向其第一个孩子节点和其右兄弟节点的指针。

//兄弟表示法
struct TreeNode {int data; //用于保存节点的数据struct TreeNode* firstChild;   //指向第一个孩子节点的指针struct TreeNode* rightSibling; //指向右边一个兄弟节点的指针
};

结构图：

树在生活中有许多的应用：

1. 文件系统： 文件系统通常以树的形式组织文件和目录。每个目录可以包含文件和子目录，形成了一个层次结构。

2. 电子游戏中的场景图： 在游戏设计中，场景图常常以树结构表示游戏场景中的对象关系和层次。

3. 组织结构： 公司或组织的层次结构可以使用树表示。每个节点可能代表一个部门，员工，或者项目。

4. 决策树： 在机器学习中，决策树用于分类和回归分析，帮助模型做出决策。

5. 图形学中的场景图： 用于表示3D场景中的对象关系，方便进行渲染和交互。

---

二、二叉树的概念及性质

2.1 二叉树的概念

二叉树是树的一种特殊情况，其中每个节点最多有两个子节点，分别是左子节点和右子节点。

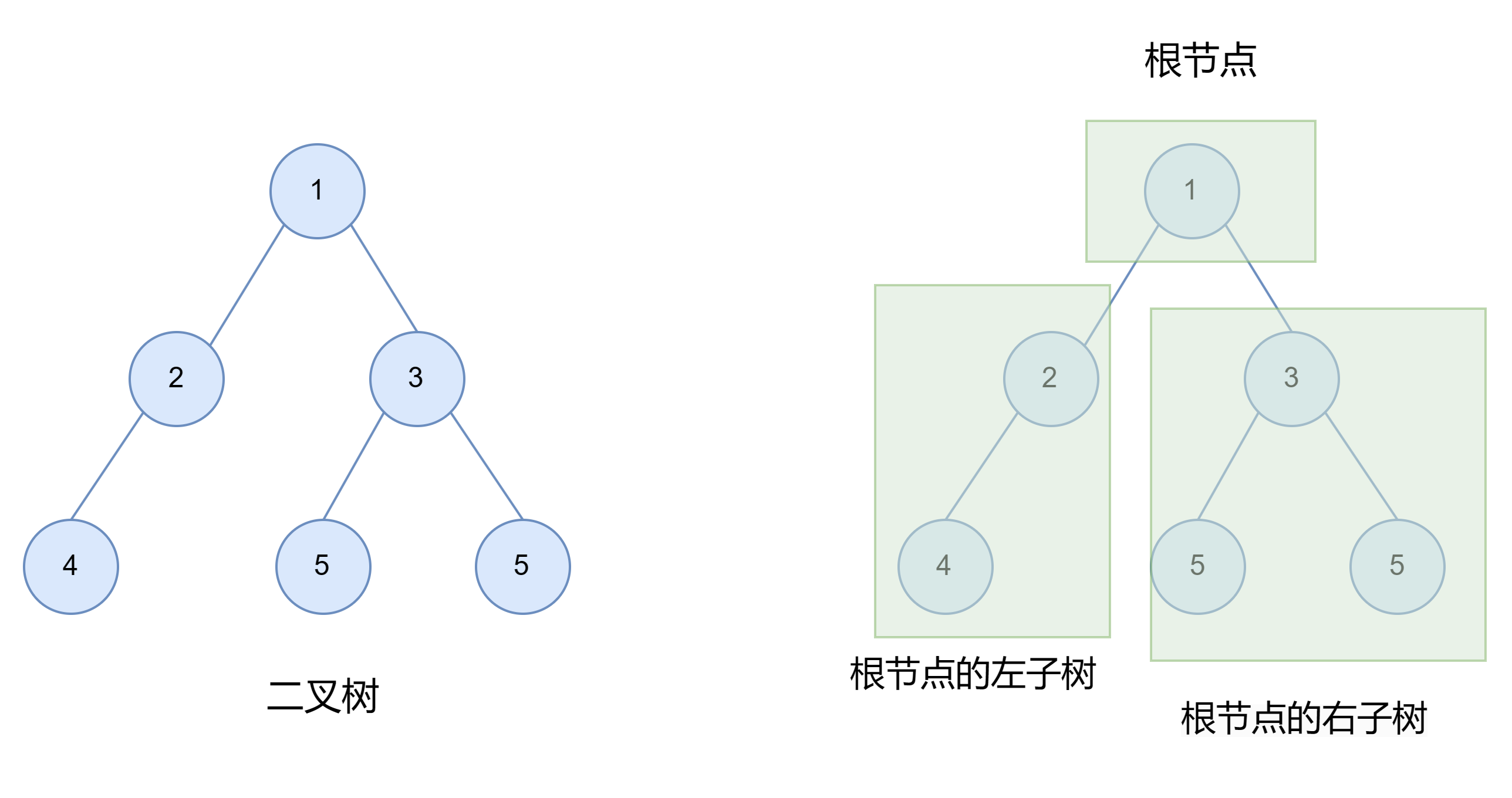
从上图可以看出：

1. 二叉树不存在度大于2的节点
2. 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树

注意：对于任意的二叉树都是由以下几种情况复合而成的：

---

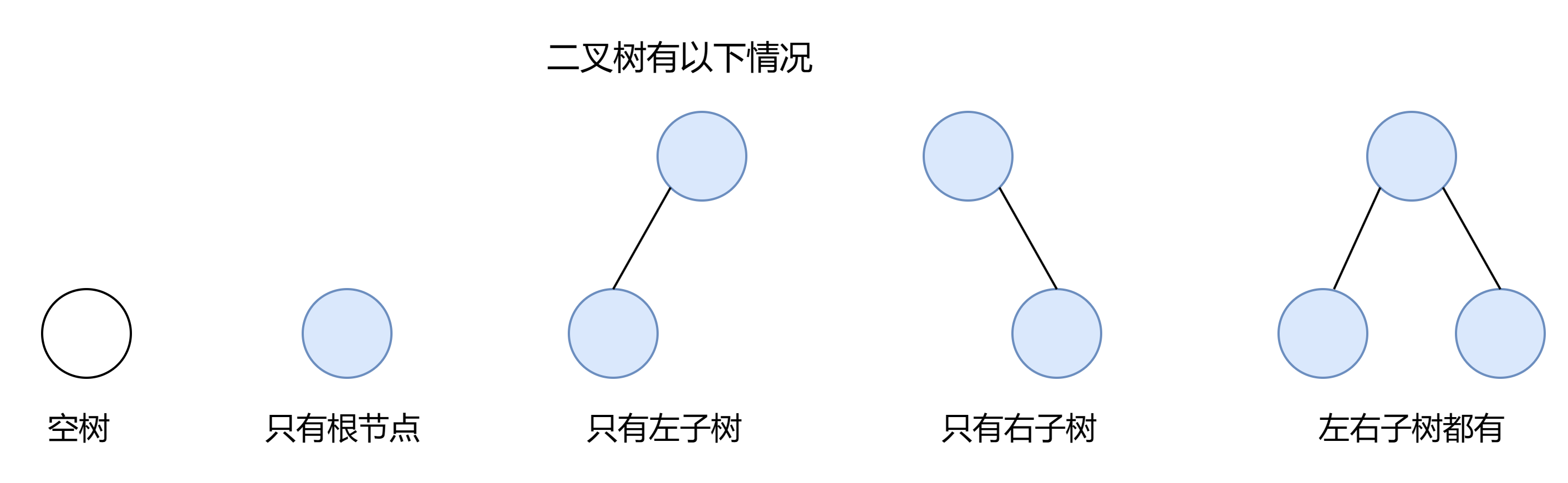
2.2 二叉树的性质

1. 满二叉树： 如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为$k$，且结点总数是$2^k-1$ ，则它就是满二叉树。
2. 完全二叉树： 完全二叉树也是一种特殊的二叉树，它和满二叉树的主要区别在于，除了最后一层，其他层的节点都是紧凑排列的，而且最后一层的节点都尽量靠左排列。如果最后一层的节点没有填满，那么缺失的节点会从左到右依次排列。 要注意的是满二叉树是一种特殊的完全二叉树。

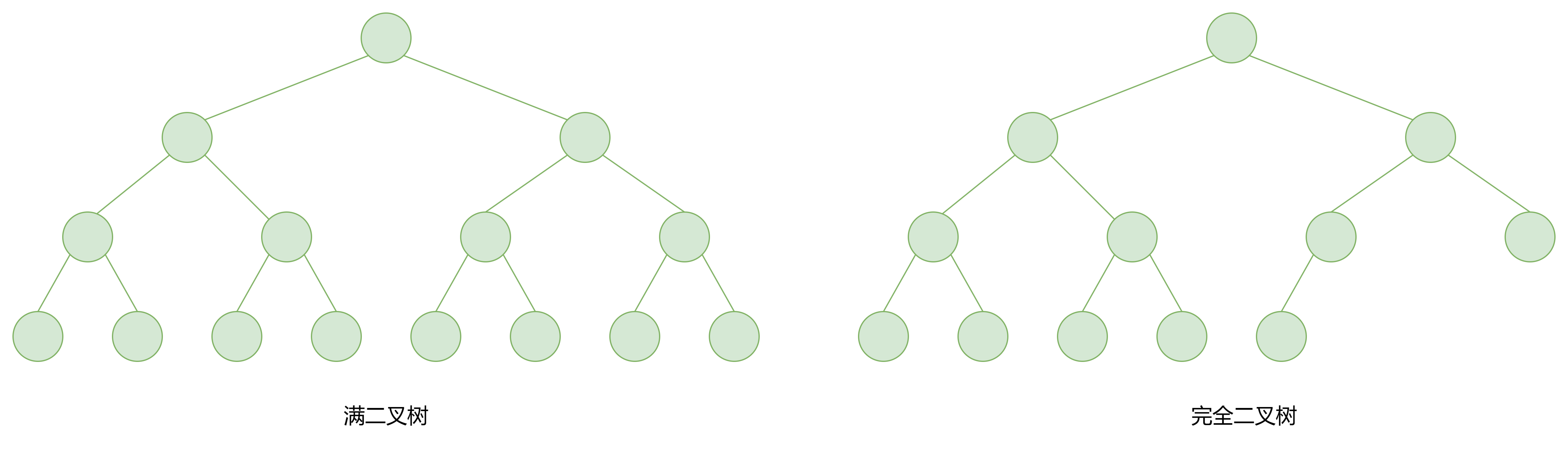
1. 若规定根节点的层数为1，则一棵非空二叉树的第$i$层上最多有 $2^{(i-1)}$个结点.
2. 若规定根节点的层数为1，则深度为h的二叉树的最大结点数是 $2^h-1$
3. 若规定根节点的层数为1，具有n个结点的满二叉树的深度，$h=lo{g}_2(n+1)$
4. 对于具有$n$个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则对于序号为i的结点有：

• 若$i>0$，$i$位置节点的双亲序号为$(i-1)/2$；$i=0$，$i$为根节点编号，无双亲节点
• 若$2i+1<=n$，左孩子序号为$2i+1$
• 若$2i+2<=n$，右孩子序号为$2i+2$

---

如果你喜欢这篇文章，点赞👍+评论+关注⭐️哦！
欢迎大家提出疑问，以及不同的见解。