文章目录
- 前言
- 一、_ZBufferParams参数有两组值
- 二、LinearEyeDepth
- 1、使用
- 2、Unity源码推导:
- 3、使用矩阵推导:
- 三、Linear01Depth
- 1、使用
- 2、Unity源码推导
- 3、数学推导:
前言
在之前的文章中,我们实现了对深度图的使用。因为,深度图不是线性的。所以,在使用时,我们使用了 Linear01Depth 函数对其进行了线性转化。
- Unity中URP下开启和使用深度图
但是,对深度图进行线性转化 还有其他函数。
在这篇文章中,我们来看一下深度图线性转化的 Linear01Depth函数 和 LinearEyeDepth 函数 干了什么。
一、_ZBufferParams参数有两组值
-
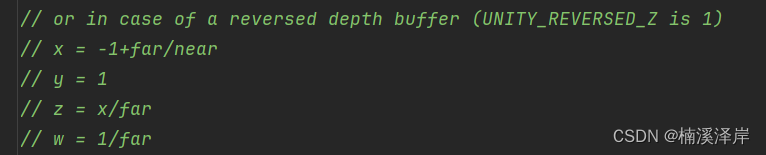
在OpenGL下

-
在类DirectX下
二、LinearEyeDepth
1、使用
-
对采样的深度图纹理进行线性转化
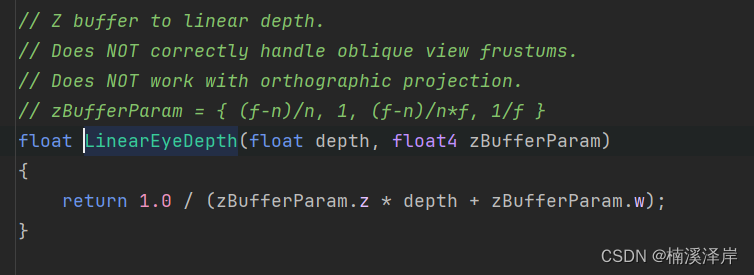
-
转化后的值,就是原来物体的深度 Z 值
float4 cameraDepthTex = SAMPLE_TEXTURE2D(_CameraDepthTexture,sampler_CameraDepthTexture,uv);
float depthTex = LinearEyeDepth(cameraDepthTex,_ZBufferParams);
- 返回结果全白,效果不明显

- 我们对其取小数部分,使其效果明显一点
frac(depthTex)

2、Unity源码推导:
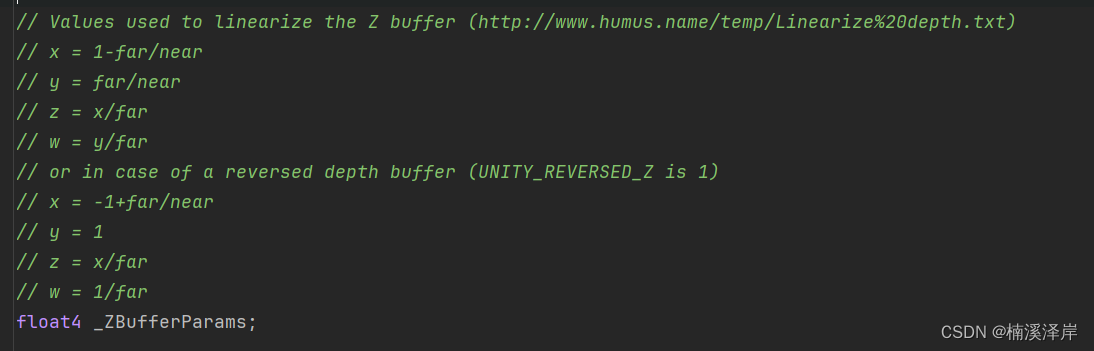
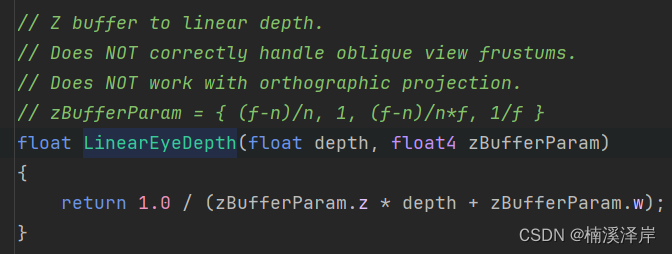
- 这里使用OpenGL下推导
Z v i e w = 1 1 − f n f d + f n f Z_{view}=\frac{1}{\frac{1-\frac{f}{n}}{f}d+\frac{\frac{f}{n}}{f}} Zview=f1−nfd+fnf1
Z v i e w = 1 ( n n − f n ) 1 f d + 1 n Z_{view}=\frac{1}{(\frac{n}{n}-\frac{f}{n})\frac{1}{f}d+\frac{1}{n}} Zview=(nn−nf)f1d+n11
Z v i e w = 1 ( n − f n ) 1 f d + 1 n Z_{view}=\frac{1}{(\frac{n-f}{n})\frac{1}{f}d+\frac{1}{n}} Zview=(nn−f)f1d+n11
Z v i e w = 1 n − f n f d + 1 n Z_{view}=\frac{1}{\frac{n-f}{nf}d+\frac{1}{n}} Zview=nfn−fd+n11
3、使用矩阵推导:
-
OpenGL
[ 2 n w 0 0 0 0 2 n h 0 0 0 0 n + f n − f 2 n f n − f 0 0 − 1 0 ] \begin{bmatrix} \frac{2n}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ 0 & 0 & \frac{n+f}{n-f} &\frac{2nf}{n-f}\\ 0 & 0 & -1 & 0\\ \end{bmatrix} w2n0000h2n0000n−fn+f−100n−f2nf0 -
DirectX
[ 2 n w 0 0 0 0 2 n h 0 0 0 0 n f − n n f f − n 0 0 − 1 0 ] \begin{bmatrix} \frac{2n}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ 0 & 0 & \frac{n}{f-n} &\frac{nf}{f-n}\\ 0 & 0 & -1 & 0\\ \end{bmatrix} w2n0000h2n0000f−nn−100f−nnf0 -
由观察空间转化到裁剪空间矩阵可得
Z c l i p = n + f n − f Z v i e w + 2 n f n − f W v i e w Z_{clip}=\frac{n+f}{n-f}Z_{view}+\frac{2nf}{n-f}W_{view} Zclip=n−fn+fZview+n−f2nfWview
W c l i p = − Z v i e w W_{clip}=-Z_{view} Wclip=−Zview -
做透视除法可得
Z n d c = Z c l i p W c l i p = n + f n − f Z v i e w + 2 n f n − f − Z v i e w = n + f f − n + 2 n f ( f − n ) Z v i e w Z_{ndc} = \frac{Z_{clip}}{W_{clip}} = \frac{\frac{n+f}{n-f}Z_{view}+\frac{2nf}{n-f}}{-Z_{view}}=\frac{n+f}{f-n}+\frac{2nf}{(f-n)Z_{view}} Zndc=WclipZclip=−Zviewn−fn+fZview+n−f2nf=f−nn+f+(f−n)Zview2nf -
d = 0.5 ⋅ Z n d c + 0.5 d=0.5·Z_{ndc}+0.5 d=0.5⋅Zndc+0.5
d = 0.5 ⋅ ( n + f f − n + 2 n f ( f − n ) Z v i e w ) + 0.5 d = 0.5·(\frac{n+f}{f-n}+\frac{2nf}{(f-n)Z_{view}})+0.5 d=0.5⋅(f−nn+f+(f−n)Zview2nf)+0.5 -
我们由 d d d 公式化简,即可得到 Z v i e w Z_{view} Zview
Z v i e w = 1 f − n n f d − 1 n Z_{view} = \frac{1}{\frac{f-n}{nf}d-\frac{1}{n}} Zview=nff−nd−n11 -
为了得到正的Z值,需要取反
Z v i e w = − 1 f − n n f d − 1 n Z_{view} =- \frac{1}{\frac{f-n}{nf}d-\frac{1}{n}} Zview=−nff−nd−n11
Z v i e w = 1 n − f n f d + 1 n Z_{view}=\frac{1}{\frac{n-f}{nf}d+\frac{1}{n}} Zview=nfn−fd+n11
三、Linear01Depth
1、使用
-
对采样的深度图纹理进行线性转化
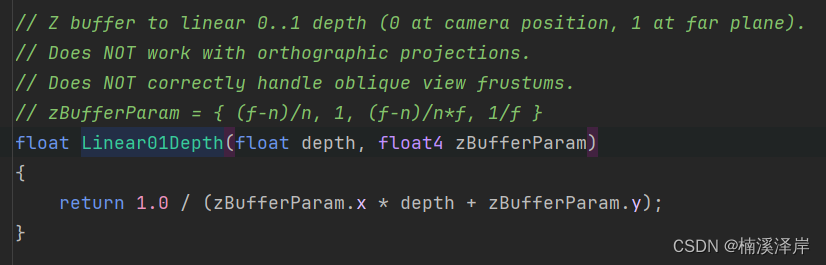
-
转化后的值,是Z值在[0,1]区间的值
float4 cameraDepthTex = SAMPLE_TEXTURE2D(_CameraDepthTexture,sampler_CameraDepthTexture,uv);
float depthTex = Linear01Depth(cameraDepthTex,_ZBufferParams);
- 返回结果

2、Unity源码推导
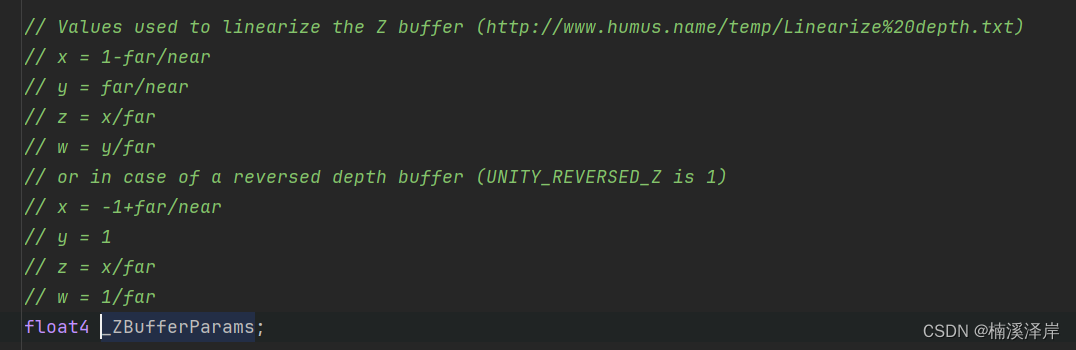
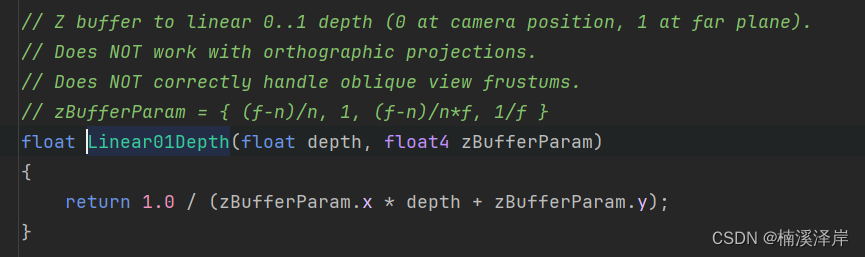
- OpenGL下推导:
Z v i e w = 1 ( 1 − f n ) d + f n Z_{view}= \frac{1}{(1-\frac{f}{n})d+\frac{f}{n}} Zview=(1−nf)d+nf1
3、数学推导:
-
这是LinearEyeDepth下推导出来的
Z v i e w = 1 n − f n f d + 1 n Z_{view}=\frac{1}{\frac{n-f}{nf}d+\frac{1}{n}} Zview=nfn−fd+n11 -
Z v i e w Z_{view} Zview的取值范围 [ n e a r , f a r ] [near,far] [near,far]
-
使其除以一个 f f f得到 Linear01Depth函数的结果
Z v i e w = 1 n − f n f d + 1 n ⋅ 1 f = 1 n − f n f d f + f n = 1 ( 1 − f n ) d + f n Z_{view}=\frac{1}{\frac{n-f}{nf}d+\frac{1}{n}}·\frac{1}{f}=\frac{1}{\frac{n-f}{nf}df+\frac{f}{n}}=\frac{1}{(1-\frac{f}{n})d+\frac{f}{n}} Zview=nfn−fd+n11⋅f1=nfn−fdf+nf1=(1−nf)d+nf1