数据结构模拟实现二叉树（孩子表示法）

一、二叉树的简单概念

（1）关于树的一些概念

（2）二叉树的一些概念及性质

定义二叉树的代码：

二、二叉树的方法实现

（1）createTree

（2）preOrder

（3）inOrder

（4）postOrder

（5）size

（6）getLeafNodeCount

（7）getKLevelNodeCount

（8）getHeight

（9）find

（10）levelOrder

（11）isCompleteTree

三、最终代码

一、二叉树的简单概念

（1）关于树的一些概念

结点的度：一个结点含有子树的个数称为该结点的度；如上图：A的度为6
树的度：一棵树中，所有结点度的最大值称为树的度；如上图：树的度为6
叶子结点或终端结点：度为0的结点称为叶结点；如上图：B、C、H、I...等节点为叶结点
双亲结点或父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点；如上图：A是B的父结点
孩子结点或子结点：一个结点含有的子树的根结点称为该结点的子结点；如上图：B是A的孩子结点
根结点：一棵树中，没有双亲结点的结点；如上图：A
结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推
树的高度或深度：树中结点的最大层次；如上图：树的高度为4
非终端结点或分支结点：度不为0的结点；如上图：D、E、F、G...等节点为分支结点
兄弟结点：具有相同父结点的结点互称为兄弟结点；如上图：B、C是兄弟结点
堂兄弟结点：双亲在同一层的结点互为堂兄弟；如上图：H、I互为兄弟结点
结点的祖先：从根到该结点所经分支上的所有结点；如上图：A是所有结点的祖先
子孙：以某结点为根的子树中任一结点都称为该结点的子孙。如上图：所有结点都是A的子孙
森林：由m（m>=0）棵互不相交的树组成的集合称为森林

（2）二叉树的一些概念及性质

概念：二叉树即为每个节点的度都小于等于2的树，即为二叉树。

性质：

1. 若规定根结点的层数为1，则一棵非空二叉树的第i层上最多有 (i>0)个结点
2. 若规定只有根结点的二叉树的深度为1，则深度为K的二叉树的最大结点数是 (k>=0)
3. 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0＝n2＋1
4. 具有n个结点的完全二叉树的深度k为上取整
5. 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的顺序对所有节点从0开始编号，则对于序号为i的结点有：
若i>0，双亲序号：(i-1)/2；i=0，i为根结点编号，无双亲结点
若2i+1<n，左孩子序号：2i+1，否则无左孩子
若2i+2<n，右孩子序号：2i+2，否则无右孩子

定义二叉树的代码：

//孩子表示法
public class MyBinomialTree {static class TreeNode {char val;TreeNode left;TreeNode right;public TreeNode(char val) {this.val = val;}}
}

二、二叉树的方法实现

（1）createTree

此方法是创建一个二叉树，里面是已经构造好了的二叉树，画图是如下情况：

代码如下：

    //创建一个二叉树TreeNode createTree() {TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');TreeNode H = new TreeNode('H');A.left = B;A.right = C;B.left = D;B.right = E;E.right = H;C.left = F;C.right = G;return A;}

在main方法中创建MyBinomialTree类的对象，调用此方法，就能创建出上面的二叉树，代码如下：

        MyBinomialTree myBinomialTree = new MyBinomialTree();MyBinomialTree.TreeNode root = myBinomialTree.createTree();

（2）preOrder

此方法是前序遍历二叉树的方法，前序遍历即为根左右的顺序遍历二叉树，上图我们创建的二叉树，前序遍历为：A B D E H C F G

代码如下：

    // 前序遍历void preOrder(TreeNode root) {if(root == null) {return;}System.out.print(root.val + " ");preOrder(root.left);preOrder(root.right);}

执行效果如下：

和上面写的顺序一样。

（3）inOrder

此方法是中序遍历的方法，中序遍历即为左根右的顺序遍历二叉树，继续照着上面的图，中序遍历为：D B E H A F C G

代码如下：

    // 中序遍历  -》 左根右void inOrder(TreeNode root){if(root == null) {return;}inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);}

执行效果如下：

和上面写的顺序一样。

（4）postOrder

此方法是后续遍历的方法，后序遍历即为左右根的顺序遍历二叉树，照着上面创建的二叉树图，后序遍历为：D H E B F G C A

代码如下：

    // 后序遍历  -》 左右根void postOrder(TreeNode root){if(root == null) {return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val + " ");}

执行效果如下：

和上面写的顺序一样。

（5）size

此方法是计算二叉树有多少个节点的方法，要计算二叉树有多少个节点，也意味着要遍历一遍二叉树，可以使用上面前中后序的任一遍历方法，用一个全局变量count1计数，如果遍历到当前节点不为空，则count++，最后返回count，代码如下：

    public static int count1 = 0;int size1(TreeNode root) {if(root == null) {return 0;}if(root != null) {count1++;}size1(root.left);size1(root.right);return count1;}

执行效果如下：

也可以使用子问题思想，二叉树的节点 = 当前root节点的左节点之和 + 当前root节点的右节点之和 + 1，如图：

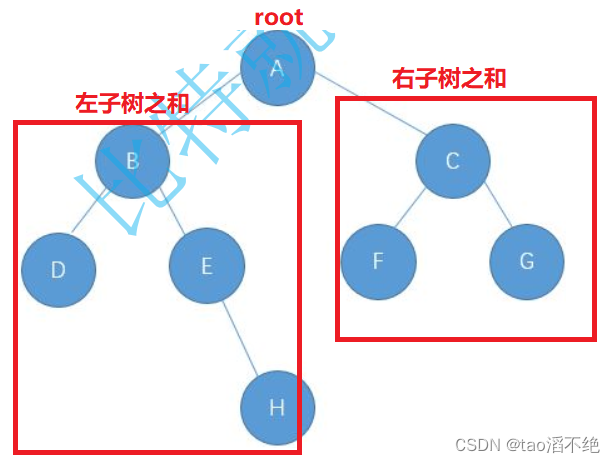左边的子树+右边的子树+root本身自己（1）

代码如下：

    // 获取树中节点的个数int size(TreeNode root) {if(root == null) {return 0;}return size(root.left) + size(root.right) + 1;}

执行效果如下：

（6）getLeafNodeCount

此方法是获取叶子节点的个数，要获取叶子节点个数，可以用遍历一遍二叉树的思想，找出二叉树那些节点即没有左孩子，也没有右孩子的节点，即叶子节点，所以要定义一个全局变量count2

代码如下：

    public static int count2 = 0;// 获取叶子节点的个数int getLeafNodeCount(TreeNode root) {if(root == null) {return 0;}if(root.left == null && root.right == null) {count2++;}getLeafNodeCount(root.left);getLeafNodeCount(root.right);return count2;}

执行效果如下：

从图中可以看出，叶子节点有4个。

子问题思路：也是需要遍历二叉树，但遍历的方式不同，如果找到是叶子节点就返回1，不是则return后面加上方法的递归，即root节点的左边子树的叶子节点+右边子树的叶子节点，如图：

代码如下：

    // 子问题思路-求叶子结点个数int getLeafNodeCount1(TreeNode root) {if(root == null) {return 0;}if(root.left == null && root.right == null) {return 1;}return getLeafNodeCount1(root.left) + getLeafNodeCount1(root.right);}

执行效果如下：

也是4个

（7）getKLevelNodeCount

此方法是获取第K层节点的个数，第K层节点的个数 = 第K-1层的所有节点的第二层节点的个数之和，如图，第三层节点的个数=第二层节点的所有节点的第一层节点的个数之和，即B节点的第一层节点之和+C节点的第一层节点之和，而第一层节点个数只能为1。

代码如下：

    // 获取第K层节点的个数int getKLevelNodeCount(TreeNode root,int k) {if(root == null) {return 0;}if(k == 1) {return 1;}return getKLevelNodeCount(root.left, k - 1) + getKLevelNodeCount(root.right, k - 1);}

执行效果如下：

从上图可以看出第三层节点有4个，和代码运行出的结果一样。

（8）getHeight

此方法是获取二叉树的高度，要获取二叉树的高度，就需要找出root节点下面每个分支的最高高度，然后再+1，如图：

很显然，上面二叉树的高度是3+1=4

代码如下：

    // 获取二叉树的高度int getHeight(TreeNode root) {if(root == null) {return 0;}if(root.left == null && root.right == null) {return 1;}return Math.max(getHeight(root.left), getHeight(root.right)) + 1;}

执行结果如下：

和预期结果一样。

（9）find

此方法是检测值为value的元素是否存在，要检查某个节点是否存在，就要对二叉树进行遍历，这里使用前序的遍历方法，但要注意，递归的时候要保存节点，所以要创建新的二叉树保存返回的节点

代码如下：

    // 检测值为value的元素是否存在TreeNode find(TreeNode root, char val) {if(root == null) {return null;}if(root.val == val) {return root;}TreeNode ret1 = find(root.left, val);if(ret1 != null) {return ret1;}TreeNode ret2 = find(root.right, val);if(ret2 != null) {return ret2;}return null;}

执行效果如下：

上面的二叉树存在 'C' 这个节点，假如找 'X' 节点，则不会存在，会是null，如图：

（10）levelOrder

此方法是层序遍历，层序遍历是从左到右，从上到下的遍历顺序，上图的二叉树层序遍历为：
A B C D E F G H

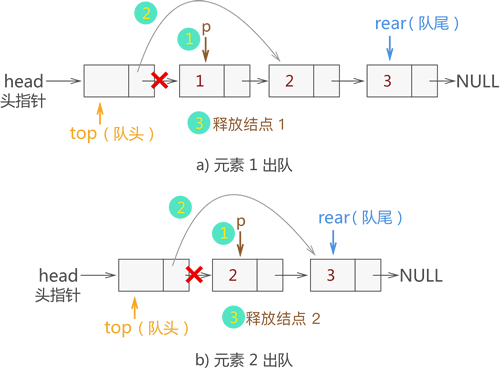
这里需要使用到队列，用上面的二叉树为例子，下面展示二叉树的节点存放进队列的顺序，如下：

先把根节点存放进队列，如下图：

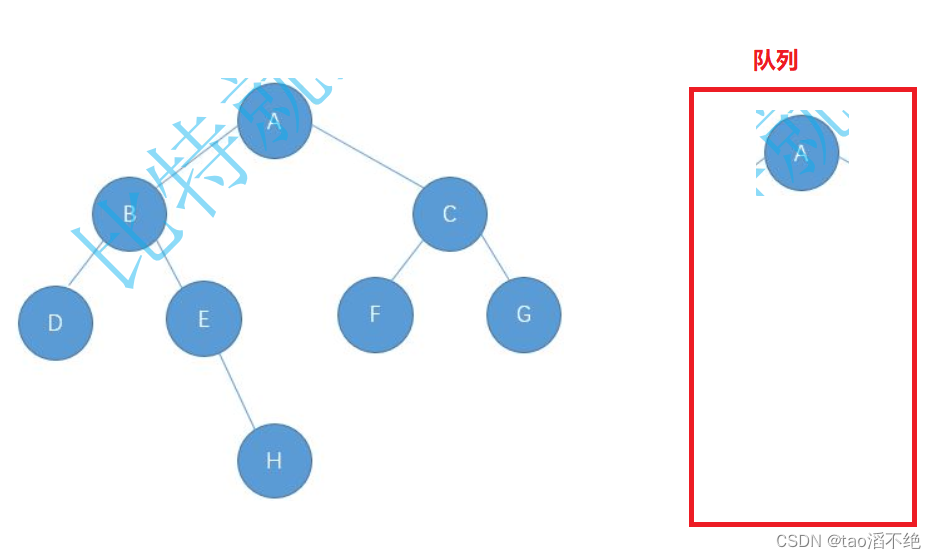
判断队列是不是空，不是空就出队列的元素，分别判断这个元素有没有左节点和右节点，如果有，就存进队列里，如下图：

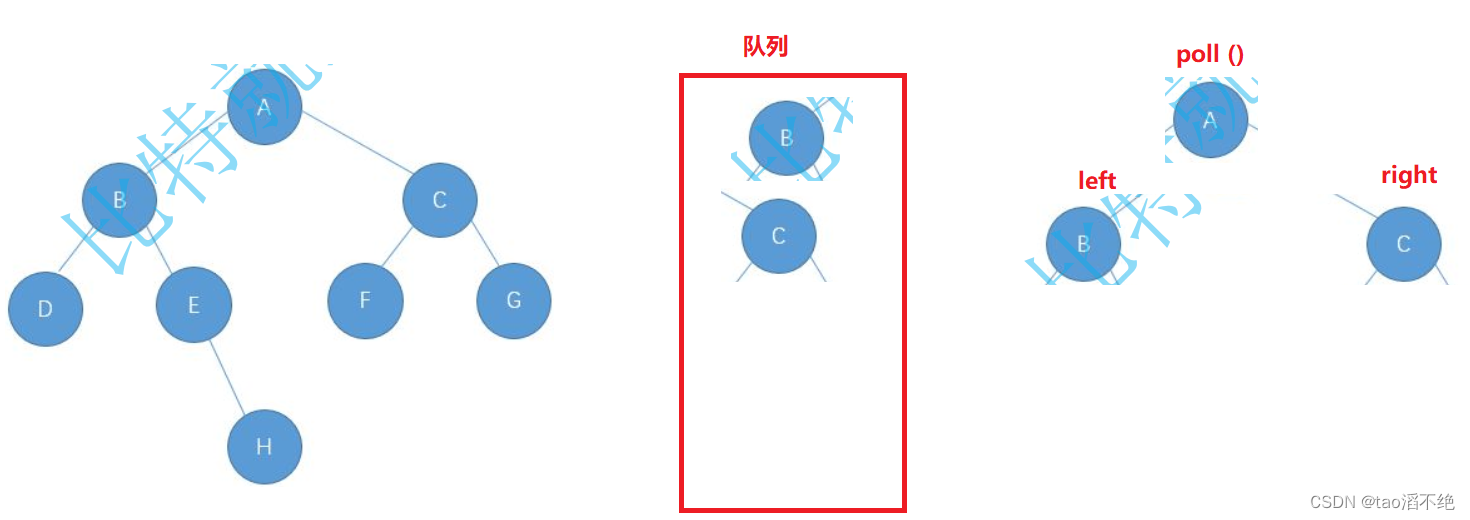
出队顶元素，次数队顶元素是B，判断B有没有左右子树，有的话分别入队列，如下图：

下一步和上面一样，如下图：

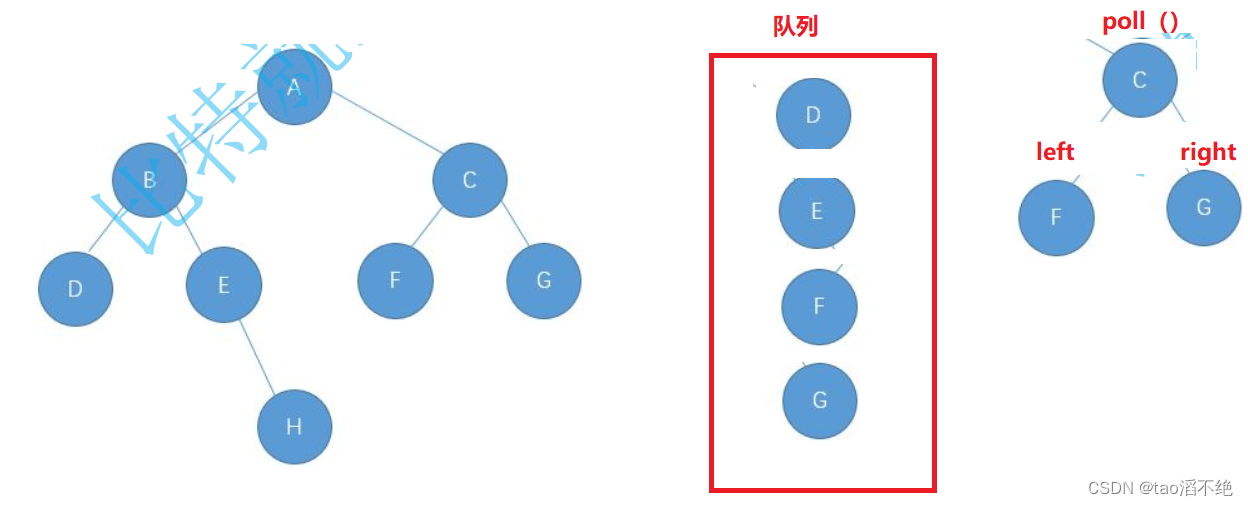
最后依次出队顶元素，再把H入队列，依次遍历，也就实现了从左到右，从上到下的遍历

代码如下：

    //层序遍历void levelOrder(TreeNode root) {//没有二叉树，直接返回if(root == null) {return;}//使用队列存放二叉树的元素Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode ret = queue.poll();System.out.print(ret.val + " ");if(ret.left != null) {queue.offer(ret.left);}if(ret.right != null) {queue.offer(ret.right);}}}

执行效果如下：

和预期结果一样。

（11）isCompleteTree

此方法是判断一棵树是不是完全二叉树，完全二叉树，即除叶子节点外，其他节点的度都为2，如下图就是完全二叉树。

但是下面的图不是完全二叉树，也是createTree方法创建的二叉树

要判断二叉树是否为完全二叉树，可以里队列，第一步骤是把二叉树层序遍历一遍：一开始把根节点root入队列，判断循环的结束条件就是队列不为空，然后找当前节点的左右子树，当前节点不为null，它的左右子树就分别存进队列，为null就直接跳出循环。这样，如果队列里有节点，即不为空的元素，则该节点不是完全二叉树，如果该队列里全是null，则是完全二叉树。因为层序遍历，如果是完全二叉树，则最后一层节点遍历完后，队列存放的元素都为null，否则不是，如图：

第二步骤是把队列里所有元素都检查一遍，如果有不为null的元素，就返回false，全为null就返回true。

代码如下：

    // 判断一棵树是不是完全二叉树boolean isCompleteTree(TreeNode root) {if(root == null) {return true;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode ret = queue.poll();if(ret != null) {queue.offer(ret.left);queue.offer(ret.right);}else {break;}}while (!queue.isEmpty()) {TreeNode ret = queue.peek();if(ret == null) {queue.poll();} else {return false;}}return true;}

使用有H节点的的createTree方法，执行效果如下：

使用没有H节点的的createTree方法，执行效果如下：

符合我们的预期效果。

三、最终代码

public class MyBinomialTree {static class TreeNode {char val;TreeNode left;TreeNode right;public TreeNode(char val) {this.val = val;}}//创建一个二叉树TreeNode createTree() {TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');TreeNode H = new TreeNode('H');A.left = B;A.right = C;B.left = D;B.right = E;//E.right = H;C.left = F;C.right = G;return A;}// 前序遍历void preOrder(TreeNode root) {if(root == null) {return;}System.out.print(root.val + " ");preOrder(root.left);preOrder(root.right);}// 中序遍历  -》 左根右void inOrder(TreeNode root){if(root == null) {return;}inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);}// 后序遍历  -》 左右根void postOrder(TreeNode root){if(root == null) {return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val + " ");}public static int count1 = 0;int size1(TreeNode root) {if(root == null) {return 0;}if(root != null) {count1++;}size1(root.left);size1(root.right);return count1;}// 获取树中节点的个数int size(TreeNode root) {if(root == null) {return 0;}return size(root.left) + size(root.right) + 1;}public static int count2 = 0;// 获取叶子节点的个数int getLeafNodeCount(TreeNode root) {if(root == null) {return 0;}if(root.left == null && root.right == null) {count2++;}getLeafNodeCount(root.left);getLeafNodeCount(root.right);return count2;}// 子问题思路-求叶子结点个数int getLeafNodeCount1(TreeNode root) {if(root == null) {return 0;}if(root.left == null && root.right == null) {return 1;}return getLeafNodeCount1(root.left) + getLeafNodeCount1(root.right);}// 获取第K层节点的个数int getKLevelNodeCount(TreeNode root,int k) {if(root == null) {return 0;}if(k == 1) {return 1;}return getKLevelNodeCount(root.left, k - 1) + getKLevelNodeCount(root.right, k - 1);}// 获取二叉树的高度int getHeight(TreeNode root) {if(root == null) {return 0;}if(root.left == null && root.right == null) {return 1;}return Math.max(getHeight(root.left), getHeight(root.right)) + 1;}// 检测值为value的元素是否存在TreeNode find(TreeNode root, char val) {if(root == null) {return null;}if(root.val == val) {return root;}TreeNode ret1 = find(root.left, val);if(ret1 != null) {return ret1;}TreeNode ret2 = find(root.right, val);if(ret2 != null) {return ret2;}return null;}//层序遍历void levelOrder(TreeNode root) {//没有二叉树，直接返回if(root == null) {return;}//使用队列存放二叉树的元素Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode ret = queue.poll();System.out.print(ret.val + " ");if(ret.left != null) {queue.offer(ret.left);}if(ret.right != null) {queue.offer(ret.right);}}}// 判断一棵树是不是完全二叉树boolean isCompleteTree(TreeNode root) {if(root == null) {return true;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode ret = queue.poll();if(ret != null) {queue.offer(ret.left);queue.offer(ret.right);}else {break;}}while (!queue.isEmpty()) {TreeNode ret = queue.peek();if(ret == null) {queue.poll();} else {return false;}}return true;}
}