给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
示例 1:
输入:nums = [1,2,0]
输出:3
示例 2:
输入:nums = [3,4,-1,1]
输出:2
示例 3:
输入:nums = [7,8,9,11,12]
输出:1
提示:
1 <= nums.length <= 5 * 105-231 <= nums[i] <= 231 - 1
解题思路:
首先,分析题目我们可以知道答案只会在1到正无穷范围内,因此可以不用管负整数和零,我们只需要从1开始逐个向后判断当前数是否存在即可,分为两个思路。
思路1:
运用哈希表,将数组中所有元素放入哈希表中,再从1开始逐个递增数,依次判断是否在哈希表中,若哈希表中未存在,则返回该数:
示例 2举例:
nums = [3,4,-1,1]
将数组元素存入哈希表中,哈希表中元素:<-1,1,3,4>
从1开始循环递增:
i=1--> 哈希表中是否存在"1" true
i=2--> 哈希表中是否存在"2" false 不存在,说明"2"即为确实的第一个正整数,结束循环并且返回2即可
代码实现1:
class Solution {public int firstMissingPositive(int[] nums) {//创建哈希表Set<Integer> hs=new HashSet<>();//遍历数组元素放入哈希表for(int x=0;x<nums.length;x++){hs.add(nums[x]);}int x;//从1开始逐个递增遍历,返回第一个哈希表里不存在的值for(x=1;;x++){if(!hs.contains(x)){break;}}return x;}
} 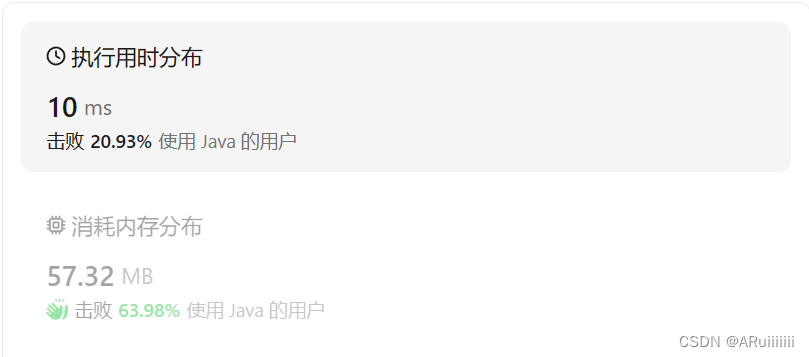
由上图的执行用时与内存消耗来看,该思路可行,但不是最优解,因此我们可以尝试用第二个方法
思路2:
利用计数排序方法解决该问题,首先我们要知道,若数组长度为5,则第一个缺失数只可能在1到6之间,因此我们可以设定一个长度为6的数组来保存数字1-6出现的次数,若未出现过则为零,返回从下标为1开始的第一个元素为零的数组下标,若都存在,则说明数组长度为第一缺失数,返回数组长度。
示例 1举例:
nums = [1,2,0]
将nums数组中元素对应到arr数组的下标,arr[nums[i]]++
如此做则数组arr: <1,1,1,0>
从arr数组下标为1开始向后逐个遍历:
arr[1]=1 > 0 已存在
arr[2]=1 > 0 已存在
arr[3]=0 = 0 不存在 因此返回数组下标,即3

还有一个问题,若是nums数组有元素大于该长度怎么办?
很简单,加个判断,因为我们已经知道第一个缺失数范围只会在1到arr数组长度之间,因此,大于这些的数目我们就不考虑,只需记录小于的即可。
代码实现2:
class Solution {public int firstMissingPositive(int[] nums) {//创建数组int missingnums[]=new int[nums.length+1];//若nums数组元素在missingnums数组下标范围内,则该下标值+1for(int x=0;x<nums.length;x++){if(nums[x]>0&&nums[x]<missingnums.length) missingnums[nums[x]]+=1;}//返回值为零的下标for(int x=1;x<missingnums.length;x++){if(missingnums[x]==0) return x;}//若所有下标值不为零,返回最后一个下标的下一个,即数组的长度return missingnums.length;}
}