Long Colorful Strip

传送门

题面翻译

题目描述

这是 F 题的第二个子任务。F1 和 F2 的区别仅在对于 $m$ 和时间的限制上

有 $n+1$ 种颜色标号从 $0$ 到 $n$，我们有一条全部染成颜色 $0$ 的长为 $m$ 的纸带。

Alice 拿着刷子通过以下的过程来给纸带染色：

我们按照从 $1$ 到 $n$ 的顺序进行染色，进行每次染色时，我们选取一个区间 $[a_i,b_i]$，$0\le a_i<b_i\le m$，并且这个区间内必定是单种颜色。

染色到最后，纸带上有各种颜色除了颜色 $0$。给出纸带最终的状态，问有多少种不同的染色方案能到达最终状态。输出时结果模 $998244353$。

输入格式

第一行有两个整数 $n$ 和 $m$，$1\le n\le 500$，$n\le m\le 10^6$。$n$ 代表除了颜色 $0$ 有多少种颜色，$m$ 代表纸带的长度。

第二行有 $m$ 个用空格分隔的整数 $c_1,c_2,\dots ,c_m$，$1<=c_i<=n$，代表完成染色后纸带的最终状态。保证最终状态中能在纸带上找到从 $1$ 到 $n$ 所有的颜色。

输出格式

输入一个单独的整数，即 Alice 可行的染色方案数模 $998244353$。

题目描述

This is the second subtask of problem F. The only differences between this and the first subtask are the constraints on the value of $m$ and the time limit. It is sufficient to solve this subtask in order to hack it, but you need to solve both subtasks in order to hack the first one.

There are $n+1$ distinct colours in the universe, numbered $0$ through $n$ . There is a strip of paper $m$ centimetres long initially painted with colour $0$ .

Alice took a brush and painted the strip using the following process. For each $i$ from $1$ to $n$ , in this order, she picks two integers $0\le a_i<b_i\le m$ , such that the segment $[a_i,b_i]$ is currently painted with a single colour, and repaints it with colour $i$ .

Alice chose the segments in such a way that each centimetre is now painted in some colour other than $0$ . Formally, the segment $[i-1,i]$ is painted with colour $c_i$ ( $c_i\ne 0$ ). Every colour other than $0$ is visible on the strip.

Count the number of different pairs of sequences { a i } i = 1 n \{a_i\}_{i=1}^n {ai​}i=1n​ , { b i } i = 1 n \{b_i\}_{i=1}^n {bi​}i=1n​ that result in this configuration.

Since this number may be large, output it modulo $998244353$ .

输入格式

The first line contains a two integers $n$ , $m$ ( $1\le n\le 500$ , $n\le m\le 10^6$ ) — the number of colours excluding the colour $0$ and the length of the paper, respectively.

The second line contains $m$ space separated integers $c_1,c_2,\dots ,c_m$ ( $1\le c_i\le n$ ) — the colour visible on the segment $[i-1,i]$ after the process ends. It is guaranteed that for all $j$ between $1$ and $n$ there is an index $k$ such that $c_k=j$ .

输出格式

Output a single integer — the number of ways Alice can perform the painting, modulo $998244353$ .

样例 #1

样例输入 #1

3 3
1 2 3

样例输出 #1

5

样例 #2

样例输入 #2

2 3
1 2 1

样例输出 #2

1

样例 #3

样例输入 #3

2 3
2 1 2

样例输出 #3

0

样例 #4

样例输入 #4

7 7
4 5 1 6 2 3 7

样例输出 #4

165

样例 #5

样例输入 #5

8 17
1 3 2 2 7 8 2 5 5 4 4 4 1 1 6 1 1

样例输出 #5

20

提示

In the first example, there are $5$ ways, all depicted in the figure below. Here, $0$ is white, $1$ is red, $2$ is green and $3$ is blue.

Below is an example of a painting process that is not valid, as in the second step the segment 1 3 is not single colour, and thus may not be repainted with colour $2$ .

In the second example, Alice must first paint segment 0 3 with colour $1$ and then segment 1 2 with colour $2$ .

解题思路

前言

Luogu居然没有搜索题解，这对萌新十分不友好，所以就由本人来贡献一篇搜索题解吧。

作者建议

该题为这题的进阶版，建议先完成这题再完成本题。

正文

本题有 $n<m$ 的情况，所以与 Short 版解法略有不同。（ Short 版做法戳这里）

先将 $c$ 数组去重，将连续的一段相同颜色并做一格，便于处理。相关代码如下：

for (int i = 1; i <= m; i++) {x = rd();if (x != a[len]) {a[++len] = x;}
}

对于 $n=m$ 的情况：

与 Short 版处理方法相同。

对于 $n<m$ 的情况：

• 记录下进过前文所描述的去重操作后数组长度，若大于 $2\times n$ 则一定无解，输出 0 ，并结束程序（否则会 RE ，本人亲测有效）。
• 在 dfs 函数中，要进行一些改动。

  • 首先，要记录该区间编号最小的颜色在整个数组中第一次与最后一次出现的位置。若其中一个不在该区间内，则该区间无符合条件的涂色方法。

  • 对于符合条件的区间，进行如下操作（为了便于讲解，先放张图）：
    

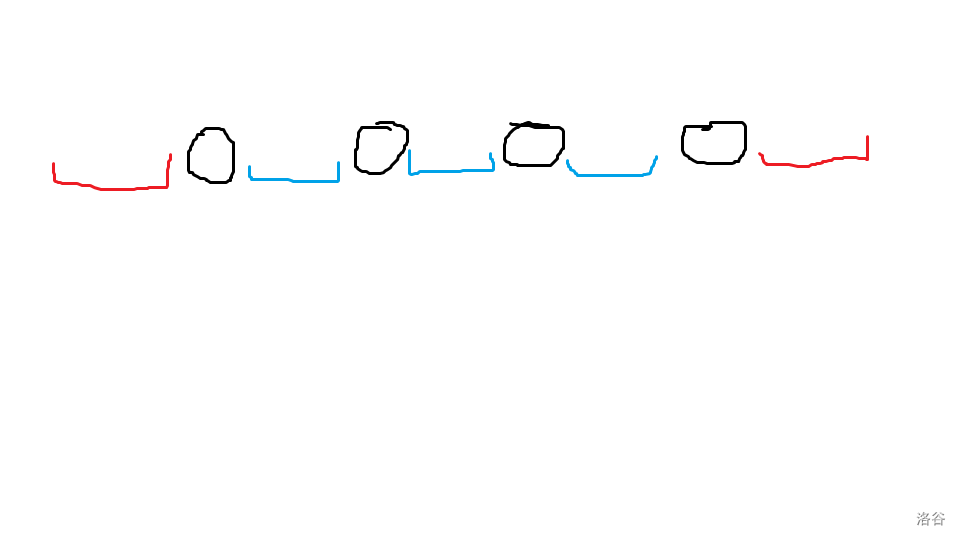
    • 对于该区间编号最小颜色第一次出现位置前于最后一次出现后的部分（红色部分），仍然照 Short 版操作：

    for (int i = l; i <= minid; i++) {tmp1 = (tmp1 + dfs(l, i - 1) * dfs(i, minidl - 1) % Mod) % Mod;
    }
    for (int i = minid; i <= r; i++) {tmp2 = (tmp2 + dfs(minidr + 1, i) * dfs(i + 1, r) % Mod) % Mod;
    }
    tong[l][r] = tmp1 * tmp2 % Mod;
    

    • 对于编号最小颜色出现位置的相隔部分（蓝色部分） ，继续放入 dfs 函数中处理，根据乘法原理，将它与 $ton{g}_{l,r}$ 相乘，就是该区间的方案数了。相关代码片段：

      for (int i = l; i <= r; i++) {if (a[i] == a[minid]) {if (top) {tong[l][r] = (tong[l][r] * (dfs(top + 1, i - 1) % Mod)) % Mod;}top = i;}}
    

• 最后， $ton{g}_{1,len}$ 就是最终总方案数了。

AC Code

#include <bits/stdc++.h>
using namespace std;
#define int long long
inline int rd() {int x = 0, f = 1;char ch = getchar();while (ch < '0' || ch > '9') {if (ch == '-')f = -1;ch = getchar();}while (ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}return x * f;
}
inline void write(int x) {if (x < 0)x = ~x + 1, putchar('-');if (x > 9) write(x / 10);putchar(x % 10 + '0');
}
const int Mod = 998244353;
const int Maxn = 2200 + 5, Maxm = 2e6 + 5;
int n, m, a[Maxm];
bool vis[Maxm];
int tong[Maxn][Maxn]/*区块l~r的方案数*/, minid, L[Maxm], R[Maxm];
inline int dfs(int l, int r) {if (tong[l][r] != -1) {return tong[l][r];} else if (l >= r) {return tong[l][r] = 1;} else {int minid = l, tmp1 = 0, tmp2 = 0, top = 0, minidl, minidr;for (int i = l; i <= r; i++) {//求当前区块编号最小颜色if (a[i] < a[minid]) {minid = i;}}minidl = L[a[minid]];minidr = R[a[minid]];if (!(l <= minidl && r >= minidr) && !(r <  minidl && l > minidr)) {return tong[l][r] = 0;}for (int i = l; i <= minid; i++) {tmp1 = (tmp1 + dfs(l, i - 1) * dfs(i, minidl - 1) % Mod) % Mod;}for (int i = minid; i <= r; i++) {tmp2 = (tmp2 + dfs(minidr + 1, i) * dfs(i + 1, r) % Mod) % Mod;}tong[l][r] = tmp1 * tmp2 % Mod;for (int i = l; i <= r; i++) {if (a[i] == a[minid]) {if (top) {tong[l][r] = (tong[l][r] * (dfs(top + 1, i - 1) % Mod)) % Mod;}top = i;}}return tong[l][r];}
}
inline void work() {memset(tong, -1, sizeof(tong));int len = 0, tmp, x;n = rd();m = rd();for (int i = 1; i <= m; i++) {x = rd();if (x != a[len]) {a[++len] = x;}}if (len > 2 * n) {cout << 0 << endl;return;}for (int i = 1; i <= len; i++) {R[a[i]] = i;}for (int i = len; i >= 1; i--) {L[a[i]] = i;}for (int i = 1; i <= len; i++) {tong[i][i] = L[a[i]] == i && R[a[i]] == i;}dfs(1, len);write(tong[1][len] % Mod);
}
signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);work();return 0;
}

不会就问问它（曾经的特邀嘉宾）