顶点
public class Vertex {String name;List<Edge> edges;// 拓扑排序相关int inDegree;int status; // 状态 0-未访问 1-访问中 2-访问过,用在拓扑排序
// dfs, bfs 相关boolean visited;//是否被访问过
// 求解最短距离相关private static final int INF = Integer.MAX_VALUE;int dist = INF;Vertex prev = null;public Vertex(String name){this.name = name;}public String getName{return name;}@Override public String toString(){return name + '('+dist+')';}@Overridepublic boolean euqals(Object o){if(this == o)return true;if(0==null||getClass()!=o.getClass())return false;Vertex vertex = (Vertex) o;return Objexts.equals(name,Vertex.name);}@Overridepublic int hashCode(){return name!=null?name.hashCode():0;}边
public class Edge {
Vertex linked;int weight;
public Edge(Vertex linked) {this(linked, 1);}
public Edge(Vertex linked, int weight) {this.linked = linked;this.weight = weight;}
}
可以处理负边 但是不能处理负环
4+-2+2+-1=3 所以没有负环
public class FloydWarshall {public static void main(String[] args) {Vertex v1 = new Vertex("v1");Vertex v2 = new Vertex("v2");Vertex v3 = new Vertex("v3");Vertex v4 = new Vertex("v4");v1.edges = List.of(new Edge(v3, -2));v2.edges = List.of(new Edge(v1, 4), new Edge(v3, 3));v3.edges = List.of(new Edge(v4, 2));v4.edges = List.of(new Edge(v2, -1));List<Vertex> graph = List.of(v1, v2, v3, v4);/*k=0直接连通v1 v2 v3 v4v1 0 ∞ -2 ∞v2 4 0 3 ∞v3 ∞ ∞ 0 2v4 ∞ -1 ∞ 0看上面那副图的权重k=1 借助v1到达其它顶点v1 v2 v3 v4v1 0 ∞ -2 ∞v2 4 0 2 ∞v3 ∞ ∞ 0 2v4 ∞ -1 ∞ 0k=2 借助v2到达其它顶点v1 v2 v3 v4v1 0 ∞ -2 ∞v2 4 0 2 ∞v3 ∞ ∞ 0 2v4 3 -1 1 0k=3 借助v3到达其它顶点v1 v2 v3 v4v1 0 ∞ -2 0v2 4 0 2 4v3 ∞ ∞ 0 2v4 3 -1 1 0k=4 借助v4到达其它顶点v1 v2 v3 v4v1 0 -1 -2 0v2 4 0 2 4v3 5 1 0 2v4 3 -1 1 0*/floydWarshall(graph);}static void floydWarshall(List<Vertex> graph) {int size = graph.size();//顶点个数int[][] dist = new int[size][size];Vertex[][] prev = new Vertex[size][size];//从哪里来// 1)初始化for (int i = 0; i < size; i++) {Vertex v = graph.get(i); // v1 (v3)内层循环顶点Map<Vertex, Integer> map = v.edges.stream().collect(Collectors.toMap(e -> e.linked, e -> e.weight));for (int j = 0; j < size; j++) {Vertex u = graph.get(j); // v3 外层循环顶点if (v == u) {dist[i][j] = 0;//相同顶点} else {dist[i][j] = map.getOrDefault(u, Integer.MAX_VALUE);prev[i][j] = map.get(u) != null ? v : null;//更新上一个顶点}}}print(prev);// 2)看能否借路到达其它顶点/*v2->v1 v1->v?dist[1][0] + dist[0][0]dist[1][0] + dist[0][1]dist[1][0] + dist[0][2]dist[1][0] + dist[0][3]*/for (int k = 0; k < size; k++) {for (int i = 0; i < size; i++) {for (int j = 0; j < size; j++) {
// dist[i][k] + dist[k][j] // i行的顶点,借助k顶点,到达j列顶点
// dist[i][j] // i行顶点,直接到达j列顶点if (dist[i][k] != Integer.MAX_VALUE &&dist[k][j] != Integer.MAX_VALUE &&dist[i][k] + dist[k][j] < dist[i][j]) {dist[i][j] = dist[i][k] + dist[k][j];prev[i][j] = prev[k][j];}}}
// print(dist);}print(prev);for(int i=0;i<size;i++){for(int j=0;j<size;j++){path(prev,graph,i,j);}}}static void path(Vertex[][] prev, List<Vertex> graph, int i, int j) {LinkedList<String> stack = new LinkedList<>();System.out.print("[" + graph.get(i).name + "," + graph.get(j).name + "] ");stack.push(graph.get(j).name);while (i != j) {Vertex p = prev[i][j];stack.push(p.name);j = graph.indexOf(p);}System.out.println(stack);}static void print(int[][] dist) {System.out.println("-------------");for (int[] row : dist) {System.out.println(Arrays.stream(row).boxed().map(x -> x == Integer.MAX_VALUE ? "∞" : String.valueOf(x)).map(s -> String.format("%2s", s)).collect(Collectors.joining(",", "[", "]")));}}static void print(Vertex[][] prev) {System.out.println("-------------------------");for (Vertex[] row : prev) {System.out.println(Arrays.stream(row).map(v -> v == null ? "null" : v.name).map(s -> String.format("%5s", s)).collect(Collectors.joining(",", "[", "]")));}}}Floyd能否判断负环
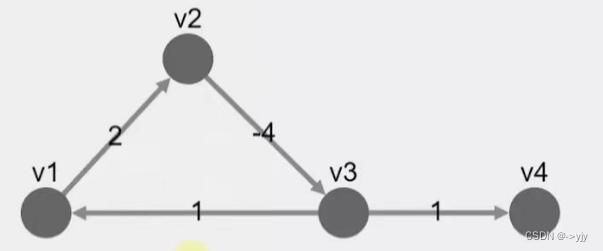
v1 v2 v3 v4
v1 0 2 ∞ ∞
v2 ∞ 0 -4 ∞
v3 1 ∞ 0 1
v4 ∞ ∞ ∞ 0
k=0
v1 v2 v3 v4
v1 0 2 ∞ ∞
v2 ∞ 0 -4 ∞
v3 1 3 0 1
v4 ∞ ∞ ∞ 0
k=1
v1 v2 v3 v4
v1 0 2 -2 -1
v2 ∞ 0 -4 ∞
v3 1 3 -1 1
v4 ∞ ∞ ∞ 0
......
负环
如果在 3 层循环结束后,在 dist 数组的对角线处(i==j 处)发现了负数,表示出现了负环