更新

补充了gpt-4版本的答案，只能说牛逼，我收回之前的替代不了高级科研工作者的结论，话不多说上答案：
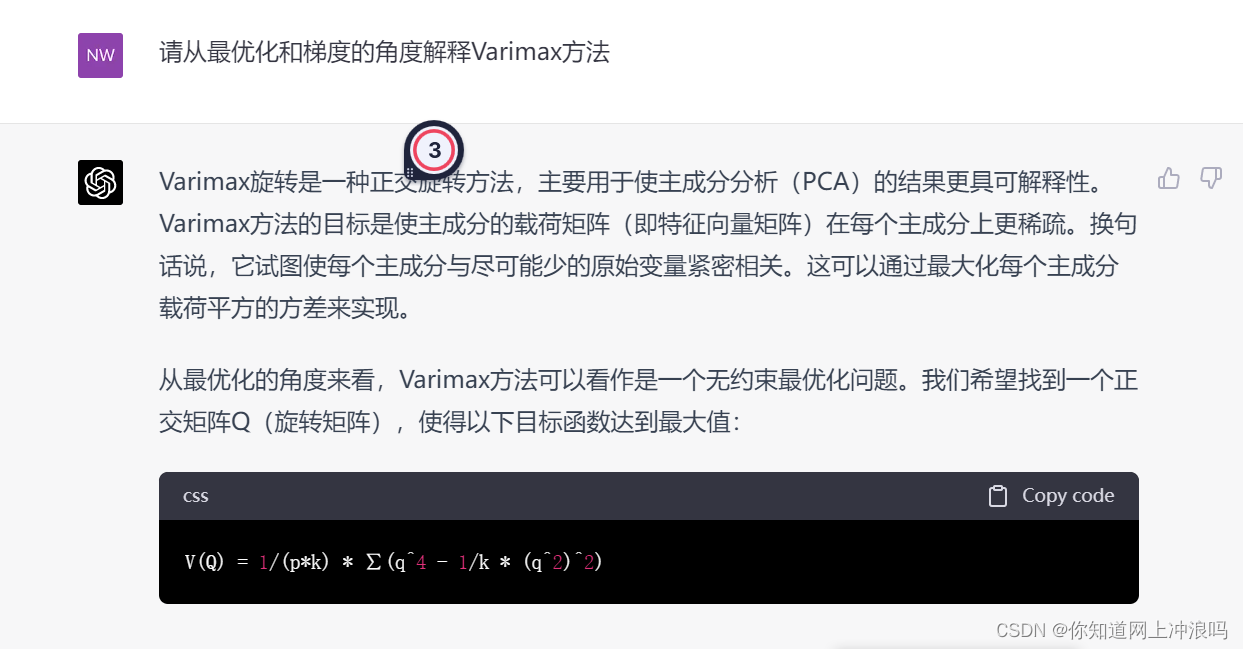
在这里插入图片描述

在这里插入图片描述
可以看到这里已经吊打got3.5了，它能把这个问题解释的很清楚了
那么关于GPF算法和varimax的关系呢

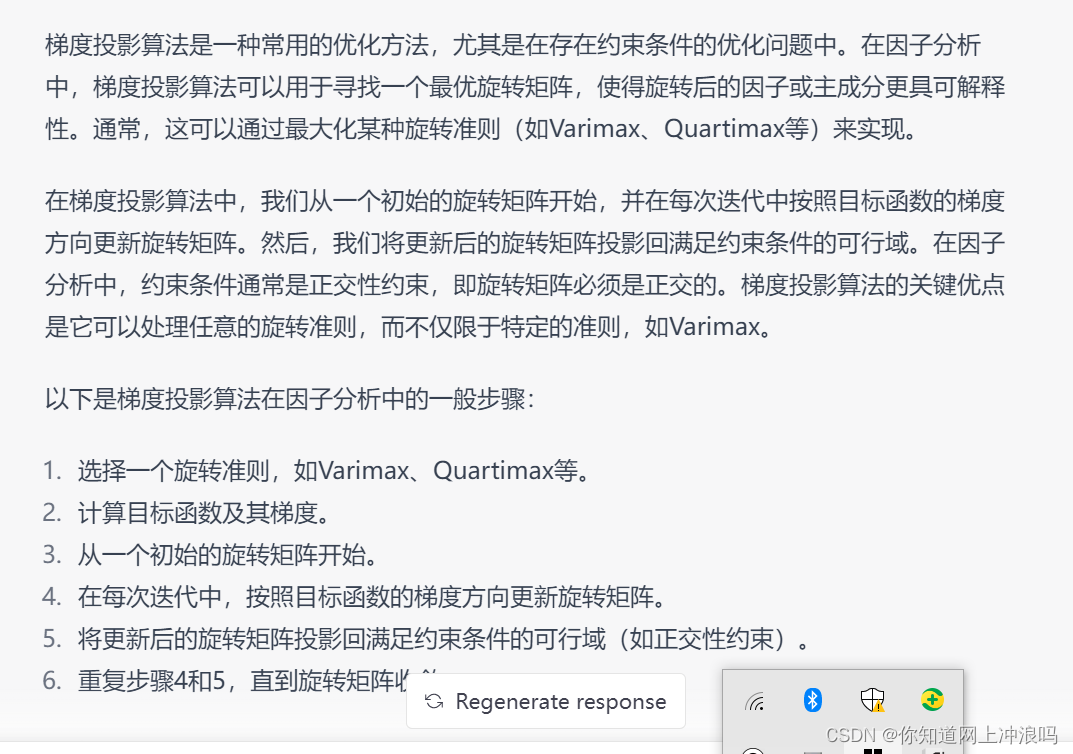
可以看到gpt3.5根本串不起来，但gpt4可以

它能改自己代码的错
并且它给出了基于scipy的一个算法，注意rpca的算法python实现大多来自github仓库这个我从来没见过：
在这里插入图片描述

import numpy as np
from scipy.optimize import minimizedef varimax_rotation(components, gamma=1.0, tol=1e-6):n, m = components.shapedef varimax_objective_function(orthogonal_matrix_flat):orthogonal_matrix = orthogonal_matrix_flat.reshape(m, m)rotated_components = components @ orthogonal_matrixvarimax_criterion = (rotated_components ** 2).sum(axis=0) - gamma / n * (rotated_components ** 4).sum(axis=0)return -varimax_criterion.sum()def orthogonality_constraint(orthogonal_matrix_flat):orthogonal_matrix = orthogonal_matrix_flat.reshape(m, m)return np.linalg.norm(orthogonal_matrix.T @ orthogonal_matrix - np.eye(m), ord='fro')initial_guess = np.eye(m).flatten()result = minimize(varimax_objective_function,initial_guess,constraints={'type': 'eq', 'fun': orthogonality_constraint},tol=tol)if not result.success:print("Warning: Varimax rotation did not converge within the specified tolerance")rotation_matrix = result.x.reshape(m, m)return components @ rotation_matrix

有点牛皮啊
接下来我让他用公式解释代码原理：
设 $\in \mathbb{R}^{p \times k}$ 为旋转前的矩阵， $\in \mathbb{R}^{p \times k}$ 为旋转后的矩阵，其中 $\in \mathbb{R}^{k \times k}$ 为正交旋转矩阵。Varimax旋转的目标是最大化以下目标函数
在这里插入图片描述
注意这个就很吊了
我们对比一下GPA论文中的算法看看它是不是在胡编乱造：

这个用矩阵符号表示的

看它继续解释
在这里插入图片描述
实际上就是计算了梯度 $\frac{\partial V}{\partial T}$ 。在这个梯度的基础上，通过奇异值分解（SVD）计算新的旋转矩阵，进而优化目标函数

测试流程

这里我们看看气象统计中的经典算法-REOF/RPCA算法，用chatgpt（3.5）当老师看看会怎么样

首先我们让他解释rpca算法流程，它讲的很清楚，实际上就是旋转基得到新基
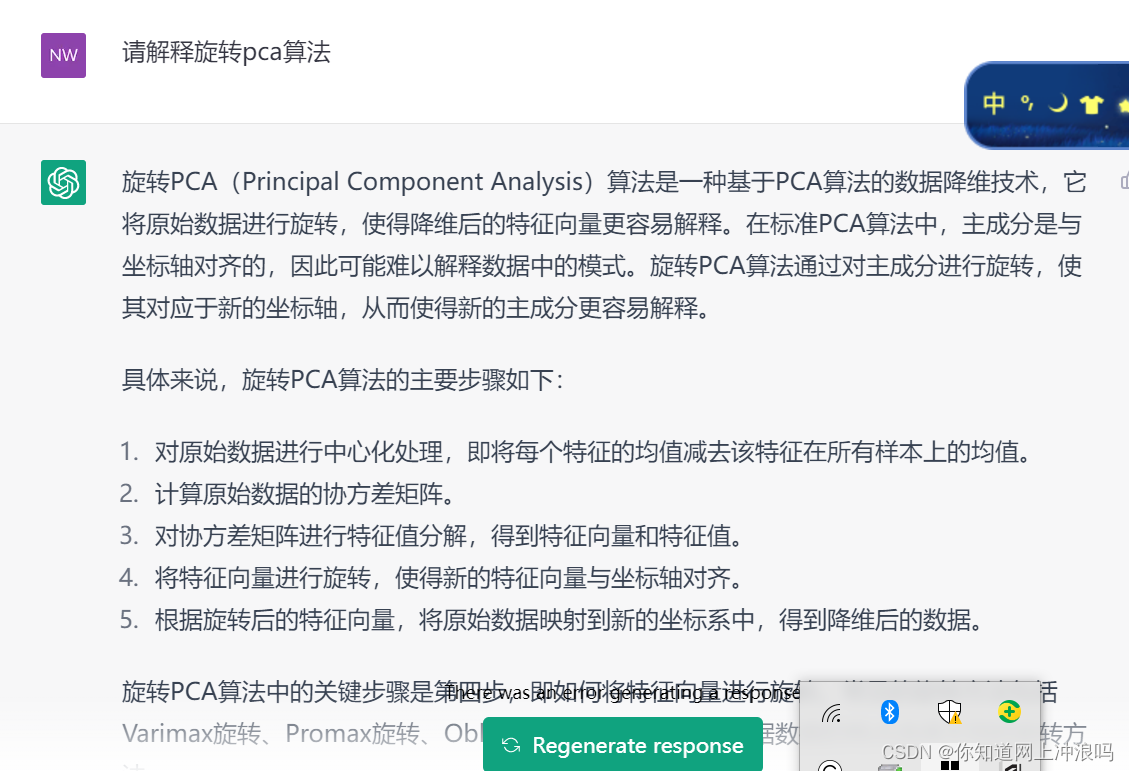
在这里插入图片描述
进一步解释varimax旋转即刚性旋转算法，讲的挺清楚哈

接下来我们让它用python实现代码：
到这里我都不怎么惊讶因为这个代码是wiki里直接抄过来的，相当于复制粘贴

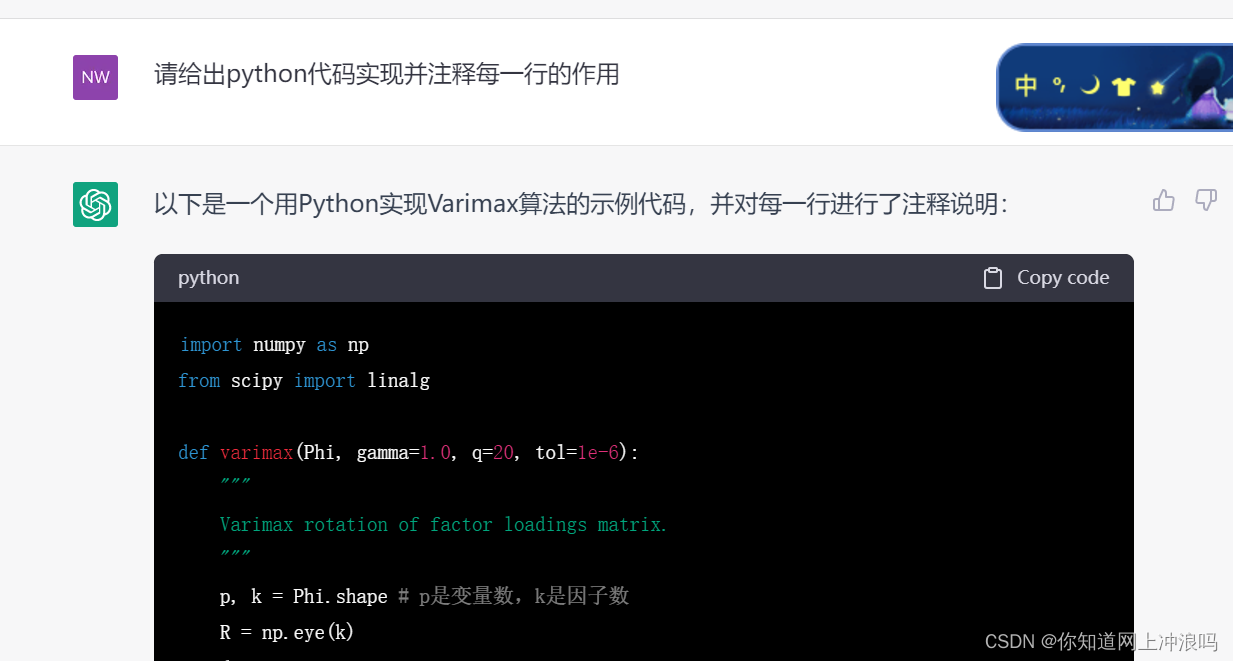
import numpy as np
from scipy import linalgdef varimax(Phi, gamma=1.0, q=20, tol=1e-6):"""Varimax rotation of factor loadings matrix."""p, k = Phi.shape # p是变量数，k是因子数R = np.eye(k)d = 0for i in range(q): # 迭代q次，直到收敛或达到最大迭代次数Phi1 = np.dot(Phi, R)tmp = np.diag(np.sum(Phi1 ** 2, axis=0)) / pU, S, V = linalg.svd(np.dot(Phi1, Phi1.T) - gamma * tmp)R = np.dot(U, V)d1 = np.sum(S)if d1 < d * (1 + tol):breakd = d1return np.dot(Phi, R)

接下来它给了逐行说明，这里解释的很清楚了，鄙人曾经在气象家园的帖子里详解了reof算法，基本上跟它这个差不多，到这里虽然觉得有点厉害但仍在我理解范围内

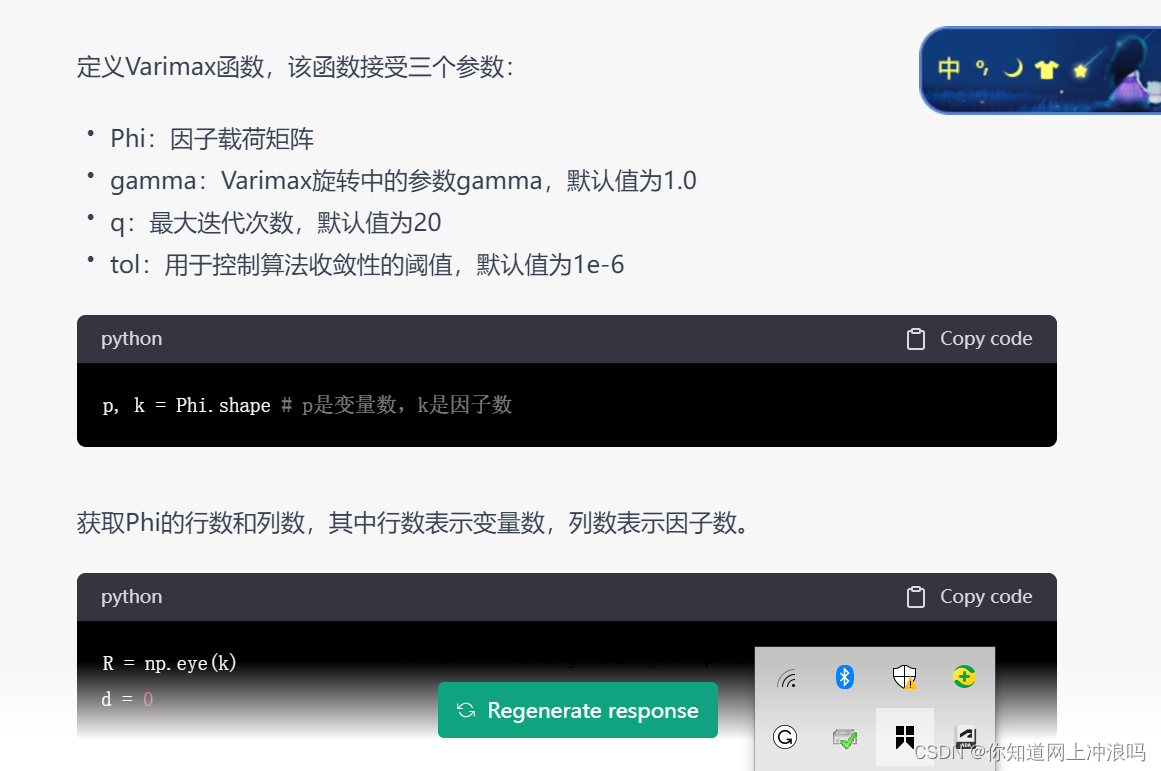
在这里插入图片描述

好家伙–注意到这里我就有些觉得恐怖了，它居然指出了算法中核心步骤：

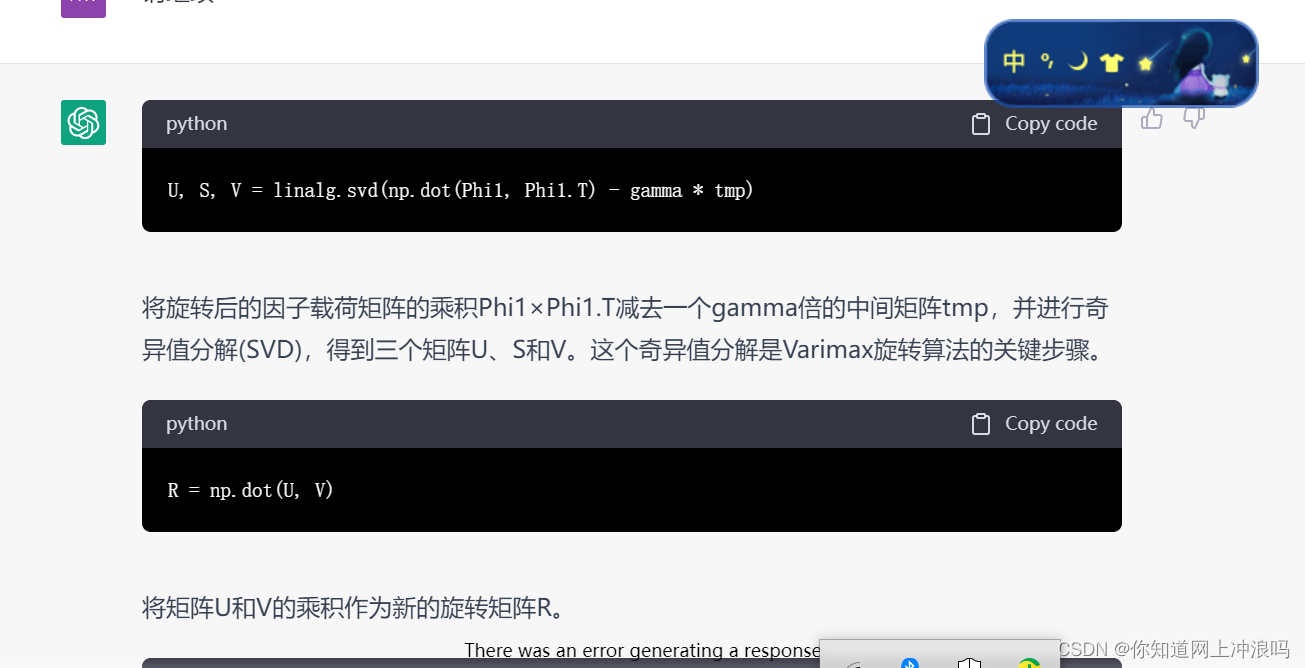
也就是为什么要奇异值分解这步，接下来我将进行诱导提问，看看他能不能讲清楚，如果能完全讲清楚，那么学校就可以完全删除统计学这门课了，因为到这里基本上是个数学不太差的工科大学牲应该都能理解

开始压力测试：
在这里插入图片描述
你搁着搁着呢？
继续诱导提问，很显然它的总结并没有涉及到问题的本质，所以我们明确的给它提出来，诱导它

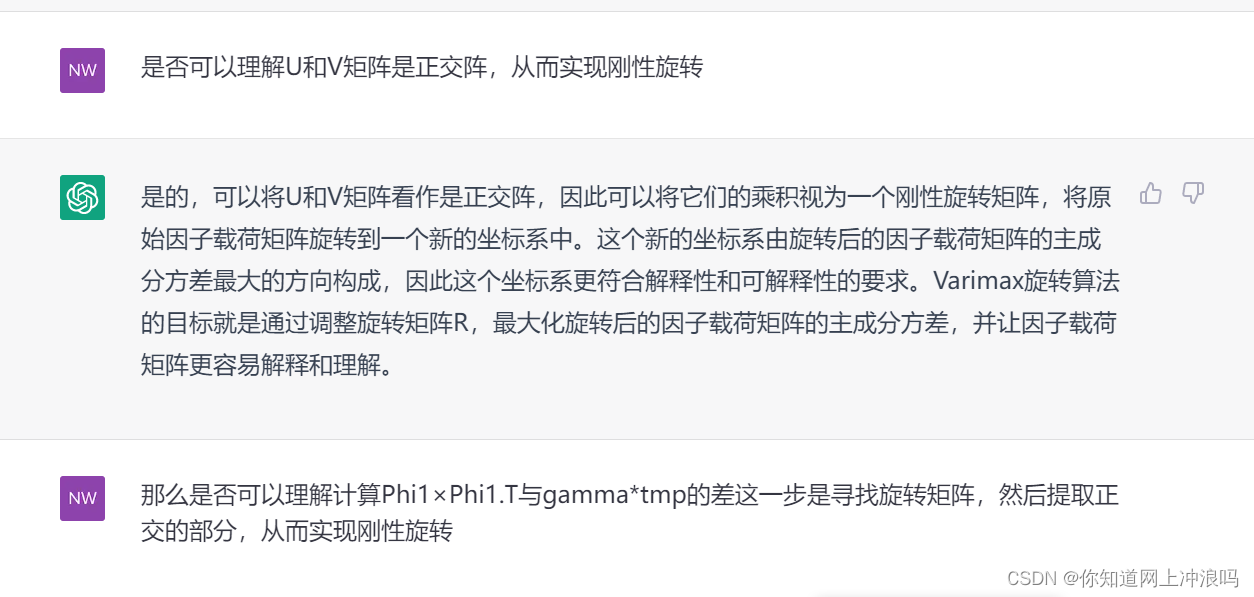
注意这是解释手段而非从设计算法的角度来解释，这里有天差地别，如果不诱导提问它是不会自己回答出来的，但到这里其实已经很离谱了，完全可以替代本科的课程了，因为它解释的很清楚了对于应用工科来说，这些完全够了

继续压力测试

我们剑指向核心
在这里插入图片描述
好家伙，干断线了，这个问题的输出极慢，我们继续搞它
实际上到这里它已经妈妈生的了

看看它到底能不能讲清楚

到这里它已经解释到了这是个最优化问题

但又妈妈生的了

那么换一种思路可以先让他了解一下啊GPA梯度投影算法

在这里插入图片描述
诱导它从最优化和梯度等关键词的角度来解释

它的回答：

在非负矩阵分解（NMF）问题中，我们希望将一个非负矩阵分解成两个非负矩阵的乘积，即 $X = W H$ ，其中 $X$ 是原始矩阵， $W$ 和 $H$ 是非负矩阵。我们通常使用最小化误差的方法来求解这个问题，即：

$\min_{W,H}||X-WH||^2_F$

其中， $||\cdot||_F$ 表示矩阵的Frobenius范数， $W$ 和 $H$ 都是非负矩阵。

从最优化问题的角度来看，上述问题等价于：

$\min_{W,H}\frac{1}{2}||X-WH||^2_F$

$s.t.\ W,H\geq 0$

其中， $s . t .$ 表示满足约束条件， $W,H\geq 0$ 表示 $W$ 和 $H$ 都是非负矩阵。

为了求解上述问题，我们可以使用梯度下降法来更新矩阵 $W$ 和 $H$ ，具体来说，我们需要计算误差矩阵 $E = X - W H$ 和梯度矩阵 $G=WEH^T$ ，然后根据学习率和梯度矩阵来更新矩阵 $W$ 和 $H$ 。

然而，在实际应用中，直接使用梯度下降法可能会导致分解结果不满足非负性约束，因此我们需要进行一些特殊的处理。其中，计算 $\Phi_1\Phi_1^T-\gamma \cdot \text{tmp}$ 这一步的作用就是为了确保分解结果满足非负性约束。

具体来说，我们首先通过将 $W$ 和 $H$ 中所有小于零的元素置为零来保证非负性约束。然后，我们可以发现，将 $W$ 和 $H$ 中所有小于零的元素置为零相当于将矩阵 $W$ 和 $H$ 投影到非负空间中，即 $W=\text{Proj}(W),H=\text{Proj}(H)$ 。因此，我们可以将梯度矩阵 $G$ 投影到切空间中，然后再将其投影到非负空间中，得到一个新的梯度矩阵 $G'=\text{Proj}{W,H}(G)$ ，其中 $\text{Proj}{W,H}(\cdot)$ 表示将矩阵投影到 $W$ 和 $H$ 的切空间中，然后再投影到非负空间中。接着，我们可以根据学习率和新的梯度矩阵 $G^{'}$ 来更新矩阵 $W$ 和 $H$ 。而计算$\Phi_1\Phi_1^T-\gamma \cdot

好家伙又断线了

让他继续解释

…然后，我们可以发现，将矩阵 $W$ 和 $H$ 中所有小于零的元素置为零相当于将矩阵 $W$ 和 $H$ 投影到非负空间中，即 $W=\text{Proj}(W),H=\text{Proj}(H)$ 。因此，我们可以将梯度矩阵 $G$ 投影到切空间中，然后再将其投影到非负空间中，得到一个新的梯度矩阵 $G'=\text{Proj}{W,H}(G)$ ，其中 $\text{Proj}{W,H}(\cdot)$ 表示将矩阵投影到 $W$ 和 $H$ 的切空间中，然后再投影到非负空间中。接着，我们可以根据学习率和新的梯度矩阵 $G^{'}$ 来更新矩阵 $W$ 和 $H$ 。

为了实现投影操作，我们可以使用旋转矩阵 $\Omega$ ，即：

$W'=W\Omega,H'=H\Omega$

其中， $\Omega$ 是一个刚性旋转矩阵，它可以将矩阵 $W$ 和 $H$ 投影到非负空间中。

我们希望找到一个最优的旋转矩阵 $\Omega$ ，使得投影后的矩阵 $W^{'}$ 和 $H^{'}$ 能够最小化误差矩阵 $E'=X-W'H'^T$ 。因此，我们可以将上述目标函数转化为：

$\min_{\Omega}\frac{1}{2}||X-W\Omega H^T\Omega^T||^2_F$

$s.t.\ \Omega\in O(k)$

其中， $O (k)$ 表示大小为 $k$ 的正交矩阵集合，即 $O(k)={\Omega\in\mathbb{R}^{k\times k}|\Omega^T\Omega=I_k}$ ， $I_k$ 表示大小为 $k$ 的单位矩阵。

将上述目标函数展开可得：

$\frac{1}{2}||X-W\Omega H^T\Omega^T||^2_F$

$=\frac{1}{2}||X-WH^T-\text{vec}(W)\text{vec}(H^T)^T\text{vec}(\Omega)\text{vec}(\Omega)^T||^2_F$

其中， $\text{vec}(A)$ 表示将矩阵 $A$ 展开成一列向量。

令 $P=\text{vec}(W)\text{vec}(H^T)^T$ ， $Q=\text{vec}(\Omega)\text{vec}(\Omega)^T$ ，则上述目标函数可以进一步化简为：

$\frac{1}{2}||X-WH^T-PQ||^2_F$

$s.t.\ Q\in O(k)$

其中， $Q\in O(k)$ 表示 $Q$ 是一个大小为 $k$ 的正交矩阵。

我们可以使用旋转矩阵的奇异值分解（SVD）来

又妈妈生的了，来继续

我们可以使用旋转矩阵的奇异值分解（SVD）来求解上述问题。具体地，我们将矩阵 $PH^T$ 做SVD分解，即：

$PH^T=USV^T$

其中， $U$ 和 $V$ 是正交矩阵， $S$ 是大小为 $r\times r$ 的对角矩阵，其中 $r$ 是矩阵 $PH^T$ 的秩。注意，我们这里使用了 $PH^T$ 的SVD分解，而不是 $P$ 和 $H$ 各自的SVD分解。这是因为我们要优化的是 $W$ 和 $H$ 的乘积 $WH^T$ ，而不是它们各自的矩阵分解。

接着，我们可以将旋转矩阵 $\Omega$ 表示为 $VU^T$ ，即：

$\Omega=VU^T$

则我们的目标函数可以进一步化简为：

$\frac{1}{2}||X-WH^T-PVU^TUVS^T||^2_F$

$=\frac{1}{2}||X-WH^T-PUVS^T||^2_F$

$s.t.\ U,V\in O(k)$

其中， $U,V\in O(k)$ 表示 $U$ 和 $V$ 是大小为 $k$ 的正交矩阵。

将上述目标函数展开，我们可以得到：

$\frac{1}{2}\text{tr}(X^TX)-\text{tr}(X^TWH^T)-\text{tr}(HWP^T)-\frac{1}{2}\text{tr}(S^TU^TV^TP^TPU^TVS)$

注意到 $\text{tr}(HWP^T)$ 和 $\text{tr}(S^TU^TV^TP^TPU^TVS)$ 不依赖于 $\Omega=VU^T$ ，因此我们可以将它们忽略，得到：

$\frac{1}{2}\text{tr}(X^TX)-\text{tr}(X^TWH^T)$

$s.t.\ U,V\in O(k)$

接下来，我们可以使用梯度下降等优化算法来求解上述目标函数，从而得到最优的旋转矩阵 $\Omega$ 。具体地，我们可以在每次迭代中使用以下更新规则：

$U\leftarrow U-\eta\frac{\partial}{\partial U}\text{tr}(X^TWH^T)$

$V\leftarrow V-\eta\frac{\partial}{\partial V}\text{tr}(X^TWH^T)$

其中， $\eta$ 是学习率， $\frac{\partial}{\partial U}\text{tr}(X^TWH^T)$ 和 $\frac{\partial}{\partial V}\text{tr}(X^TWH^T)$ 分别是目标函数对 $U$ 和 $V$ 的梯度。在每次迭代中，我们可以将 $U$ 和 $V$ 更新为它们的投影矩阵，以保证它们满足$U,V

同时是正交矩阵。

接下来，我们考虑如何计算目标函数对 $U$ 和 $V$ 的梯度。具体地，我们可以使用梯度投影算法（Gradient Projection Algorithm，GPA）来计算梯度。GPA是一种基于投影的优化算法，它可以将一个点投影到一个约束集上，从而得到在该约束集上的最优解。

在本问题中，我们的约束集是 $U,V\in O(k)$ ，即 $U$ 和 $V$ 是大小为 $k$ 的正交矩阵。因此，我们需要将梯度投影到正交矩阵集合 $O (k)$ 上。

具体地，我们可以将 $U$ 和 $V$ 写成特征值分解的形式：

$U=Q\Lambda U^T$

$V=Q\Gamma V^T$

其中， $Q$ 是正交矩阵， $\Lambda$ 和 $\Gamma$ 是对角矩阵， $U^T$ 和 $V^T$ 是 $U$ 和 $V$ 的转置矩阵。

接着，我们可以计算目标函数对 $U$ 和 $V$ 的梯度，分别为：

$\frac{\partial}{\partial U}\text{tr}(X^TWH^T)=-(XWH^T-XUU^TXWH^T)$

$\frac{\partial}{\partial V}\text{tr}(X^TWH^T)=-(XWH^T-XV\Gamma\Gamma^TV^TXWH^T)$

接下来，我们将梯度投影到正交矩阵集合 $O (k)$ 上，即求解以下最小化问题：

$\min_{Q,\Lambda}\frac{1}{2}||Q\Lambda U^TXWH^T-XWH^TU\Lambda^TQ^T||^2_F$

$s.t.\ Q\in O(k),\Lambda\in\mathbb{R}^{k\times k}$

这是一个典型的最小化问题，可以使用特征值分解等方法求解。具体地，我们可以将矩阵 $U^TXWH^T$ 做特征值分解，即：

$U^TXWH^T=UDU^T$

其中， $D$ 是对角矩阵， $U$ 是正交矩阵。然后，我们可以将 $Q$ 和 $\Lambda$ 分别设置为 $U$ 的前 $k$ 个特征向量和对应的特征值，即：

$Q = U (:, 1 : k)$

$\Lambda=\text{diag}(D_{1:k,1:k})$

这样，我们就得到了最小化问题的最优解。最后，我们可以将 $U$ 和 $V$ 分别更新为 $QU^T$ 和 $Q\Gamma V^T$ ，即：

$U\leftarrow QU^T$

$V\leftarrow Q\Gamma V^T$

这样，我们就得到了更新后的 $U$ 和 $V$ ，从而得到了更新后的旋转矩阵$\Omega=VU

它终于bb完了，下来就是关键时刻，看看它能不能串起来

在这里插入图片描述
好吧它开始胡言乱语了
开始胡给代码了
在一次迭代中，梯度的方向并不一定是旋转矩阵。假设我们在当前迭代中希望找到一个旋转矩阵 $R$ ，使得目标函数 $Q$ 最小化。在某个旋转矩阵 $R_0$ 的位置，我们可以计算出目标函数 $Q$ 在 $R_0$ 处的梯度 $G$ ，并沿着梯度的反方向移动一定距离 $\alpha$ ，得到新的旋转矩阵 $R_1 = R_0 - \alpha G$ 。这里梯度 $G$ 的方向不一定是旋转矩阵的方向，因为梯度方向只是指向最小值方向的一个向量，而旋转矩阵是由一系列矩阵乘法组成的，不一定与梯度方向一致。