难度参考
难度:简单
分类:熟悉OJ与IDE的操作
难度与分类由我所参与的培训课程提供,但需要注意的是,难度与分类仅供参考。以下内容均为个人笔记,旨在督促自己认真学习。
题目
| A + B | 1. A + B - AcWing题库 |
| 财务管理 | 1004:财务管理 |
| 实现四舍五入 | 实现四舍五入 |
| 牛牛的字符菱形 | 牛牛的字符菱形 |
题解
A+B

#include <iostream>
#include <cstdio>using namespace std;int a,b;
int main(){cin>>a>>b;cout<<a+b<<endl;return 0;
}时间复杂度为O(1)。
空间复杂度也是O(1)。
本题据说还有十几种其他恶搞版题解,待学成之后仔细研究一下。
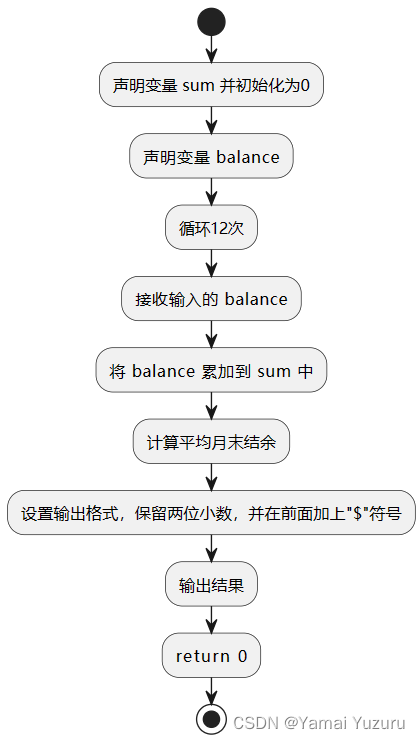
财务管理
#include <iostream>
#include <iomanip> // 用于设置输出格式using namespace std;int main() {double sum = 0.0; // 初始化总结余为0double balance; // 用于存储每个月的结余for (int i = 0; i < 12; i++) {cin >> balance; // 输入每个月的结余sum += balance; // 累加到总结余中}double average = sum / 12.0; // 计算平均月末结余// 设置输出格式,保留两位小数,并在前面加上"$"符号cout << fixed << setprecision(2) << "$" << average << endl;return 0;
}时间复杂度为O(1)。(循环次数固定)
空间复杂度也是O(1)。
使用iomanip库,可以直接用fixed去保留小数个数。
实现四舍五入
使用cmath库的话,里面有直接的四舍五入的函数。
#include <iostream>
#include <cmath>
using namespace std;int main() {double floatingNumber;cin >> floatingNumber;// 将浮点数四舍五入并转换为整数int roundedNumber = round(floatingNumber);cout << roundedNumber << endl;return 0;
}时间复杂度为O(1)。
空间复杂度也是O(1)。
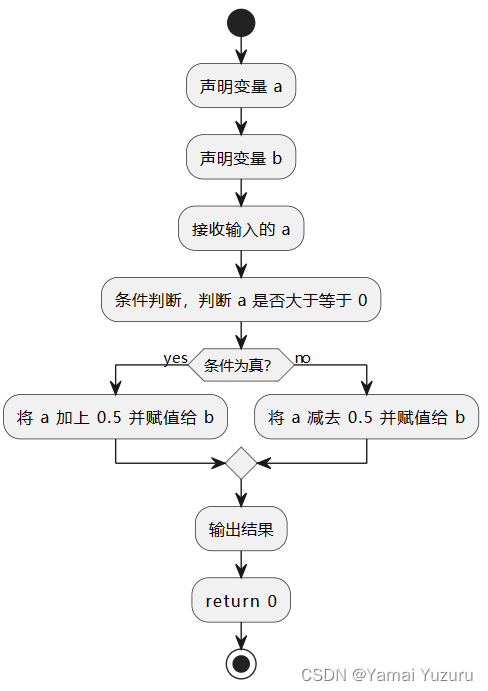
不过常见的做法是利用加减0.5后强制转化后实现四舍五入。加减的原因是正数为加,负数为减。
#include <iostream>
using namespace std;int main() {float a;int b;cin >> a;// 判断浮点数的小数部分是否大于等于0.5if (a >= 0) {b = a + 0.5;} else {b = a - 0.5;}cout << b << endl;return 0;
}时间复杂度为O(1)。
空间复杂度也是O(1)。
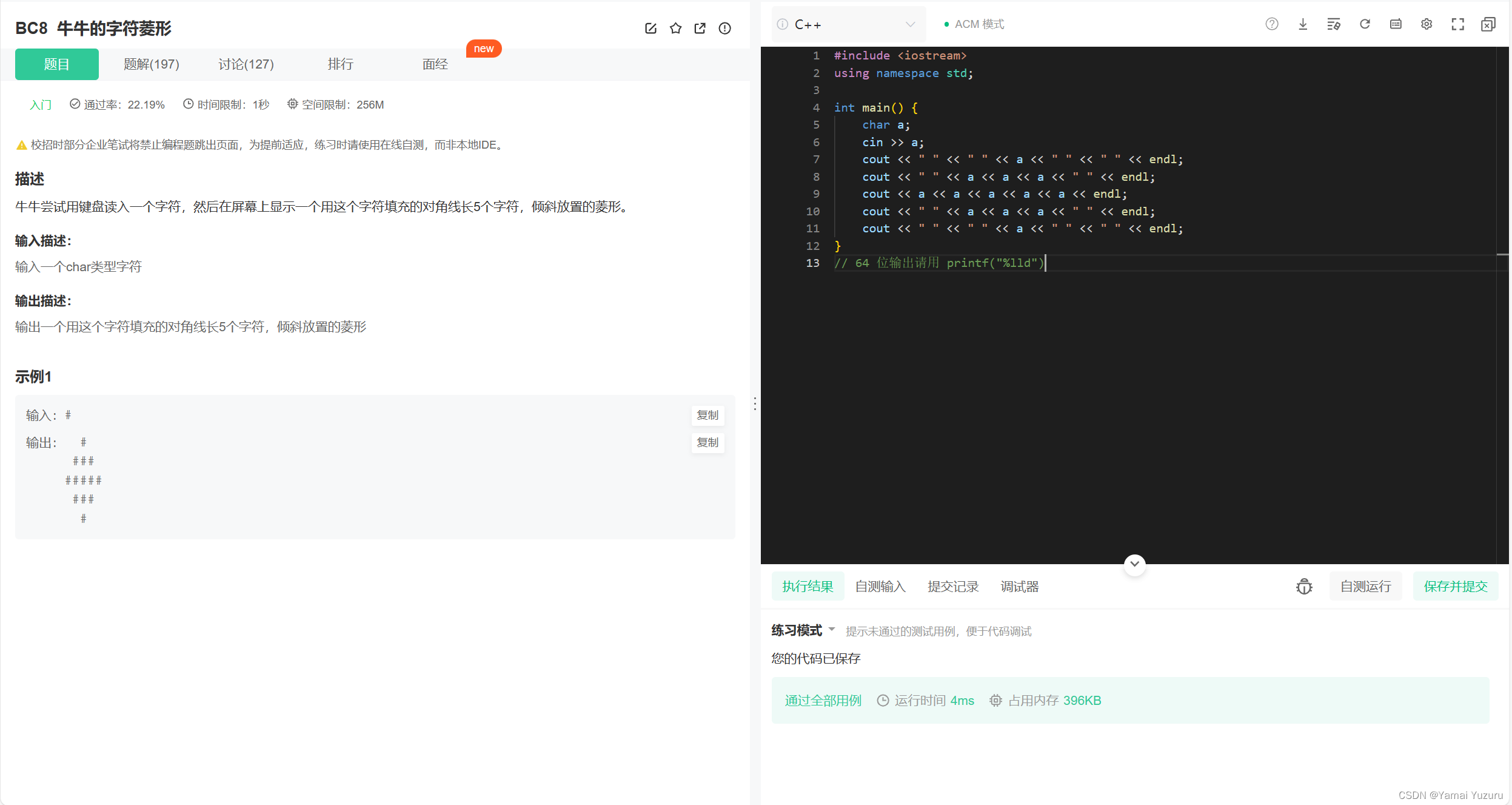
牛牛的字符菱形
明显的懒鬼做法。
#include <iostream>
using namespace std;int main() {char a;cin >> a;cout << " " << " " << a << " " << " " << endl;cout << " " << a << a << a << " " << endl;cout << a << a << a << a << a << endl;cout << " " << a << a << a << " " << endl;cout << " " << " " << a << " " << " " << endl;
}
时间复杂度为O(1)。
空间复杂度也是O(1)。
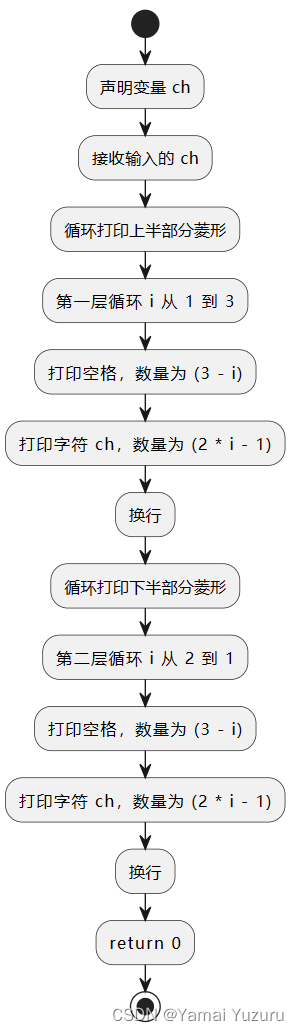
动点脑子。
#include <iostream>
using namespace std;int main() {char ch;cin >> ch;// 上半部分菱形for (int i = 1; i <= 3; i++) {for (int j = 1; j <= 3 - i; j++) {cout << " ";}for (int j = 1; j <= 2 * i - 1; j++) {cout << ch;}cout << endl;}// 下半部分菱形for (int i = 2; i >= 1; i--) {for (int j = 1; j <= 3 - i; j++) {cout << " ";}for (int j = 1; j <= 2 * i - 1; j++) {cout << ch;}cout << endl;}return 0;
}思路
-
首先,我们从用户那里接收一个字符作为输入,并将其存储在变量
ch中。 -
然后,我们使用两个循环来打印菱形图案。上半部分的循环用于打印每一行的空格和字符,下半部分的循环用于打印下半部分的空格和字符。
-
对于上半部分的循环,我们使用一个外层循环来迭代打印每一行。循环变量
i的范围是从1到3,即打印3行。每一行前面的空格的数量是3 - i,通过内层循环来输出。 -
内层循环使用变量
j从1递增到(2 * i - 1)来打印每一行的字符(ch)。这是因为每一行的字符数量符合等差数列的规律,首项是 1,公差是 2。 -
上半部分的循环结束后,我们开始打印下半部分的菱形图案。这里我们使用一个外层循环来迭代打印每一行。循环变量
i的范围是从2到1,即打印2行。每一行前面的空格的数量是3 - i,通过内层循环来输出。 -
内层循环同样使用变量
j从1递增到(2 * i - 1)来打印每一行的字符(ch)。 -
最后,我们通过输出换行符来确保每一行之后都换行。
打卡
A+B
财务管理

实现四舍五入

牛牛的字符菱形