往期文章(希望小伙伴们在看这篇文章之前,看一下往期文章)
(1)递归、搜索与回溯算法(专题零:解释回溯算法中涉及到的名词)【回溯算法入门必看】-CSDN博客
(2)递归、搜索与回溯算法(专题一:递归)-CSDN博客
深搜是实现递归的一种方式,接下来我们之间从题入手,深入浅出地了解深搜吧!
目录
1. 计算布尔二叉树的值
2. 求根结点到叶结点的数字之和
3. 二叉树剪枝
4. 验证二叉搜索树
5. 二叉搜索树中第k小的元素
6. 二叉树的所有路径
1. 计算布尔二叉树的值
力扣题目链接
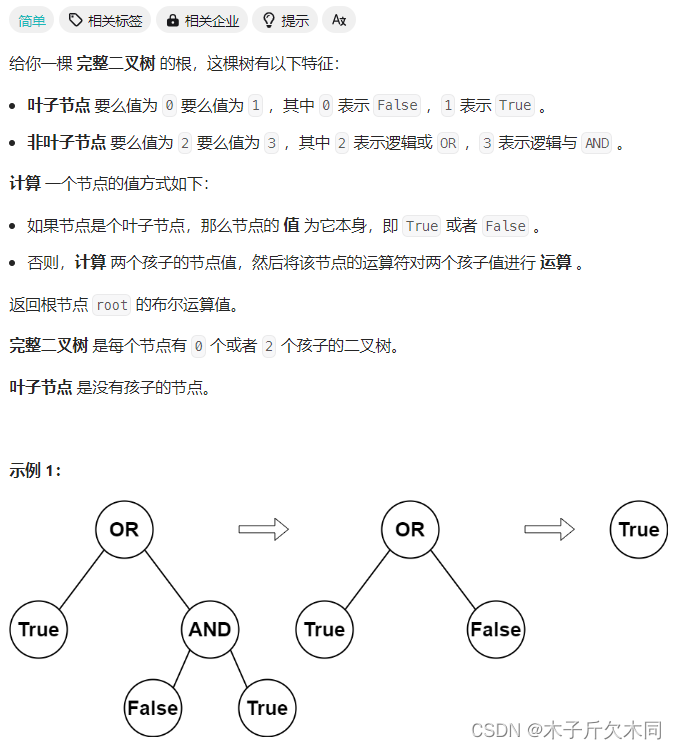

解析:
(1)函数头设计
需要根结点,故函数头为:dfs(TreeNode root);
(2)函数体设计(无条件相信这个“黑盒”,他能帮你将每个相同的子问题稳妥地解决!!!)

① 接收左子树传过来的值:boolean leftTree = dfs(root.left);
② 接收右子树传过来的值:boolean rightTree = dfs(root.right);
③ leftTree ——> root.val <—— rightTree 得到最终结果。
(3)递归出口
到叶子结点就是应该结束递归,开始回溯。
public boolean evaluateTree(TreeNode root) {//递归出口//到了叶子结点if(root.left == null){if(root.val == 0)return false;elsereturn true;}//开始递归boolean leftTree = evaluateTree(root.left);boolean rightTree = evaluateTree(root.right);if(root.val == 2){return leftTree || rightTree;}else{return leftTree && rightTree;}}
2. 求根结点到叶结点的数字之和
力扣题目链接

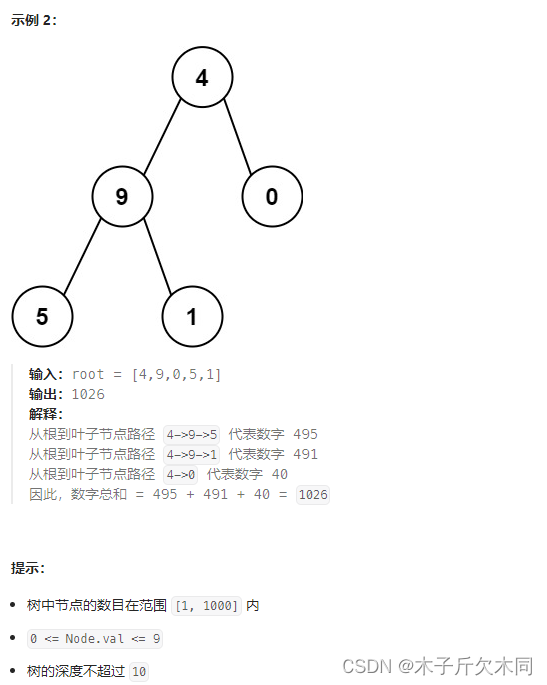
解析:
前序遍历按照根节点、左⼦树、右⼦树的顺序遍历⼆叉树的所有节点,通常⽤于⼦节点的状态依赖于⽗节点状态的题⽬。
在前序遍历的过程中,我们可以往左右⼦树传递信息,并且在回溯时得到左右⼦树的返回值。递归函数可以帮我们完成两件事:
(1)将⽗节点的数字与当前节点的信息整合到⼀起,计算出当前节点的数字,然后传递到下⼀层进⾏递
归;
(2)当遇到叶⼦节点的时候,就不再向下传递信息,⽽是将整合的结果向上⼀直回溯到根节点。
在递归结束时,根节点需要返回的值也就被更新为了整棵树的数字和。
递归函数设计:int dfs(TreeNode root,int num)
(1)返回值:当前⼦树计算的结果(数字和);
(2)参数num:递归过程中往下传递的信息(⽗节点的数字);
(3)函数作⽤:整合⽗节点的信息与当前节点的信息计算当前节点数字,并向下传递,在回溯时返回当前⼦树(当前节点作为⼦树根节点)数字和。
递归函数流程:
(1)当遇到空节点的时候,说明这条路从根节点开始没有分⽀,返回0;
(2)结合⽗节点传下的信息以及当前节点的val,计算出当前节点数字sum;
(3)如果当前结点是叶⼦节点,直接返回整合后的结果sum;
(4)如果当前结点不是叶⼦节点,将?sum?传到左右⼦树中去,得到左右⼦树中节点路径的数字和,然后相加后返回结果。
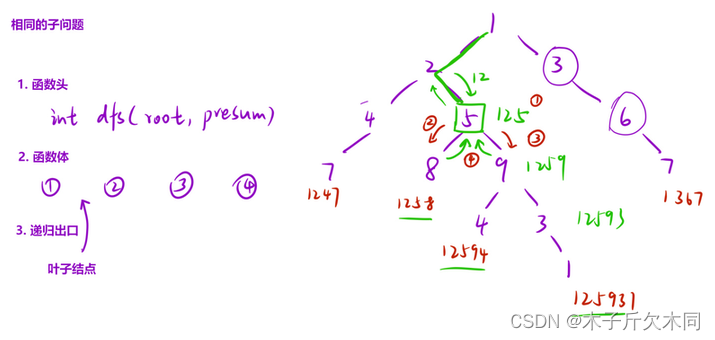
① 将自身的值并入;② 将自己本身的数字并入后走左子树;③ 将自己本身的数字并入后走右子树;④ 左右子树的结果,然后向上返回。
public int sumNumbers(TreeNode root) {return dfs(root,0);//从个位数开始}public int dfs(TreeNode root,int perSum){//一:将自身的值并入perSum = perSum * 10 + root.val;//四:递归出口:看看是不是叶子结点了,如果是,就向上返回if(root.left == null && root.right == null){return perSum;}//二:走左子树int ret = 0;if(root.left != null){ret += dfs(root.left,perSum);}//三:走右子树if(root.right != null){ret += dfs(root.right,perSum);}return ret;}
3. 二叉树剪枝
力扣题目链接
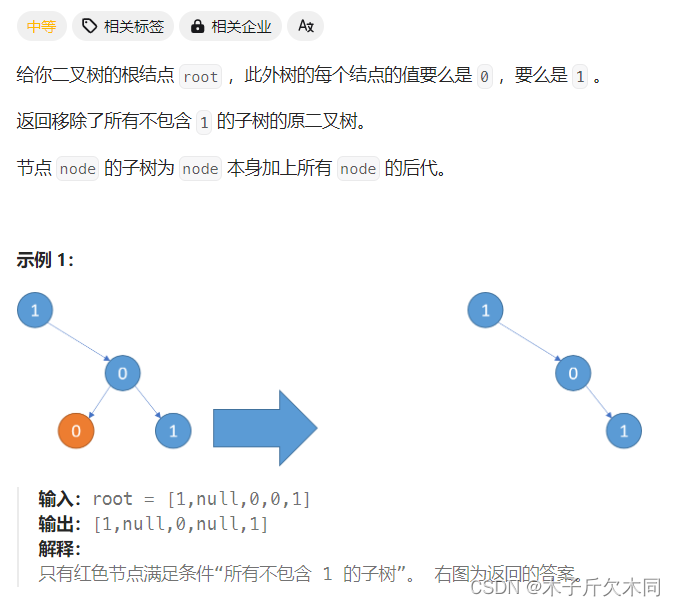


解析:
后序遍历按照左⼦树、右⼦树、根节点的顺序遍历⼆叉树的所有节点,通常⽤于⽗节点的状态依赖于⼦节点状态的题⽬。
(1)如果我们选择从上往下删除,我们需要收集左右⼦树的信息,这可能导致代码编写相对困难。然⽽,通过观察我们可以发现,如果我们先删除最底部的叶⼦节点,然后再处理删除后的节点,最终的结果并不会受到影响。
(2)因此,我们可以采⽤后序遍历的⽅式来解决这个问题。在后序遍历中,我们先处理左⼦树,然后处理右⼦树,最后再处理当前节点。在处理当前节点时,我们可以判断其是否为叶⼦节点且其值是否为0。如果满⾜条件,我们可以删除当前节点。
• 需要注意的是,在删除叶⼦节点时,其⽗节点很可能会成为新的叶⼦节点。因此,在处理完⼦节点后,我们仍然需要处理当前节点。这也是为什么选择后序遍历的原因(后序遍历⾸先遍历到的⼀定是叶⼦节点)。
• 通过使⽤后序遍历,我们可以逐步删除叶⼦节点,并且保证删除后的节点仍然满⾜删除操作的要
求。这样,我们可以较为⽅便地实现删除操作,⽽不会影响最终的结果。
• 若在处理结束后所有叶⼦节点的值均为1,则所有⼦树均包含1,此时可以返回。
递归函数头设计:void dfs(TreeNode root)
(1)返回值:⽆;
(2)参数:当前需要处理的节点;
(3)函数作⽤:判断当前节点是否需要删除,若需要删除,则删除当前节点。
后序遍历的主要流程(函数体):
(1)递归出⼝:当传⼊节点为空时,不做任何处理;
(2)递归处理左⼦树;
(3)递归处理右⼦树;
(4)处理当前节点:判断该节点是否为叶⼦节点(即左右⼦节点均被删除,当前节点成为叶⼦节点),并且节点的值为0:
- 如果是,就删除掉;
- 如果不是,就不做任何处理。
public TreeNode pruneTree(TreeNode root) {//递归出口if(root == null){return null;}//判断左子树root.left = pruneTree(root.left);//判断右子树root.right = pruneTree(root.right);//判断if(root.left == null && root.right == null && root.val == 0){root = null;}return root;}
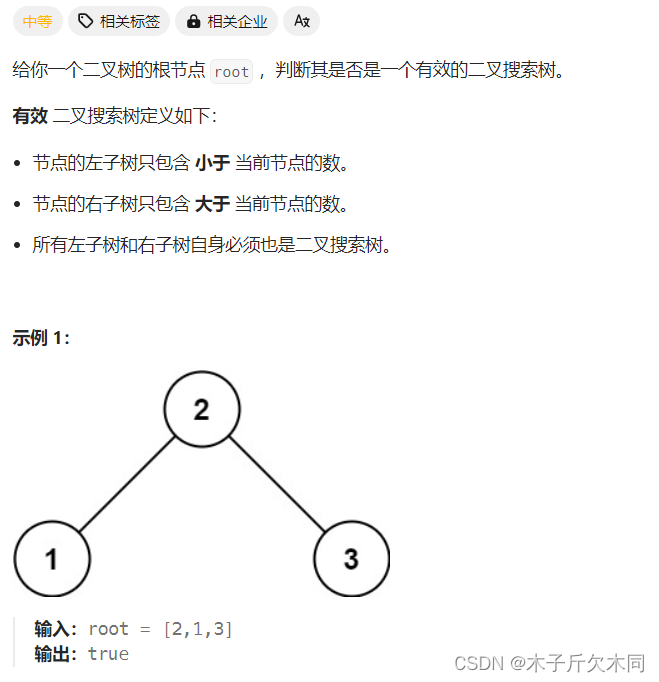
4. 验证二叉搜索树
力扣题目链接

解析:
中序遍历按照左⼦树、根节点、右⼦树的顺序遍历⼆叉树的所有节点,通常⽤于⼆叉搜索树相关题
⽬。
(1)如果⼀棵树是⼆叉搜索树,那么它的中序遍历的结果⼀定是⼀个严格递增的序列。
(2)因此,我们可以初始化⼀个⽆穷⼩的全区变量,⽤来记录中序遍历过程中的前驱结点。那么就可以在中序遍历的过程中,先判断是否和前驱结点构成递增序列,然后修改前驱结点为当前结点,传⼊下⼀层的递归中。
算法流程:
(1)初始化⼀个全局的变量prev,⽤来记录中序遍历过程中的前驱结点的val;
(2)中序遍历的递归函数中:
① 设置递归出⼝:root == null 的时候,返回true;(叶子结点本身就是一棵二叉搜索树)
② 先递归判断左⼦树是否是⼆叉搜索树,⽤left标记;
③ 然后判断当前结点是否满⾜⼆叉搜索树的性质;
▪ 如果当前结点的val⼤于prev,说明满⾜条件,将prev改为root.val;
▪ 如果当前结点的val⼩于等于prev,说明不满⾜条件,return false;
最后递归判断右⼦树是否是⼆叉搜索树,⽤right标记;
(3)只有当left和right都是true的时候,才返回true。
long prev = Long.MIN_VALUE;//存放上一个结点的值public boolean isValidBST(TreeNode root) {if(root == null)return true;//递归判断左子树boolean left = isValidBST(root.left);if(prev < root.val)prev = root.val;//判断当前节点是否为二叉搜索树,右边就不需要搞elsereturn false;//剪枝,剪掉右子树的判断if(left == false)return false;//递归判断右子树,告诉父节点,我不是二叉搜索树,你也不是boolean right = isValidBST(root.right);if(left == true && right == true)return true;elsereturn false;}
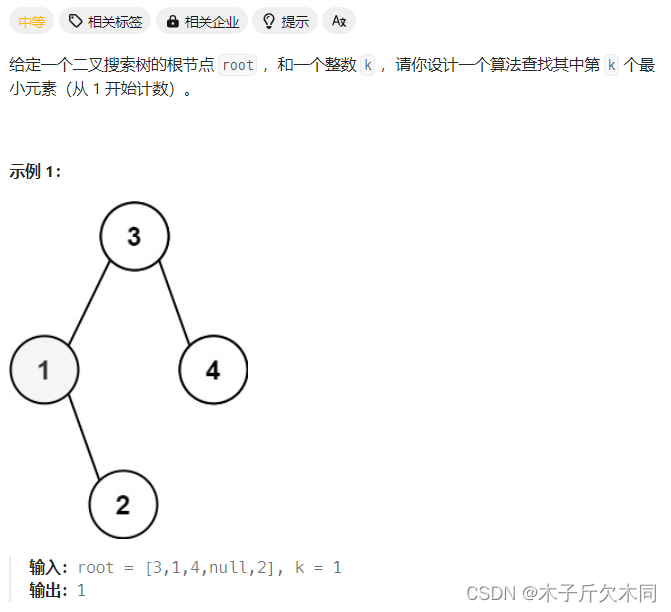
5. 二叉搜索树中第k小的元素
力扣题目链接

解析:
中序遍历 + 计数器剪枝
我们可以根据中序遍历的过程,只需扫描前k个结点即可。
因此,我们可以创建⼀个全局的计数器count,将其初始化为k,每遍历⼀个节点就将count--。直到某次递归的时候,count的值等于1,说明此时的结点就是我们要找的结果。
int ret = 0;//用来存储最终结果int count;//用来表示要找第几个结点public int kthSmallest(TreeNode root, int k) {count = k;dfs(root);return ret;}public void dfs(TreeNode root){if(root == null)return;dfs(root.left);count--;if(count == 0){ret = root.val;}dfs(root.right);}
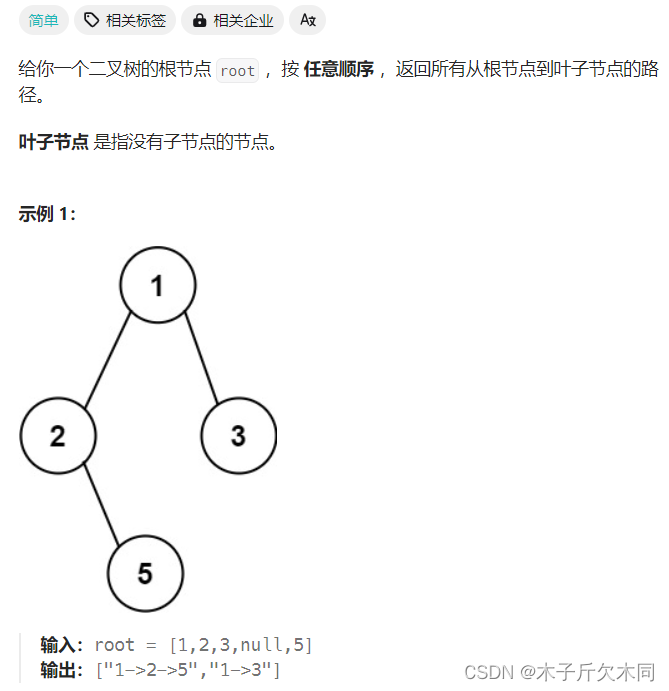
6. 二叉树的所有路径
力扣题目链接

解析:
使⽤深度优先遍历(DFS)求解。
路径以字符串形式存储,从根节点开始遍历,每次遍历时将当前节点的值加⼊到路径中,如果该节点为叶⼦节点,将路径存储到结果中。否则,将"->"加⼊到路径中并递归遍历该节点的左右⼦树。
定义⼀个结果数组,进⾏递归。递归具体实现⽅法如下:
(1)如果当前节点不为空,就将当前节点的值加⼊路径path中,否则直接返回;
(2)判断当前节点是否为叶⼦节点,如果是,则将当前路径加⼊到所有路径的存储数组paths中;
(3)否则,将当前节点值加上"->"作为路径的分隔符,继续递归遍历当前节点的左右⼦节点;
(4)返回结果数组;
注:特别地,我们可以只使⽤⼀个字符串存储每个状态的字符串,在递归回溯的过程中,需要将路径中的当前节点移除,以回到上⼀个节点。
具体实现⽅法如下:
(1)定义⼀个结果数组和⼀个路径数组。
(2)从根节点开始递归,递归函数的参数为当前节点、结果数组和路径数组。
① 如果当前节点为空,返回。
② 将当前节点的值加⼊到路径数组中。
③ 如果当前节点为叶⼦节点,将路径数组中的所有元素拼接成字符串,并将该字符串存储到结果
数组中。
④ 递归遍历当前节点的左⼦树。
⑤ 递归遍历当前节点的右⼦树。
⑥ 回溯,将路径数组中的最后⼀个元素移除,以返回到上⼀个节点。
List<String> ret;public List<String> binaryTreePaths(TreeNode root) {ret = new ArrayList<>();dfs(root,new StringBuffer());return ret;}public void dfs(TreeNode root,StringBuffer curPath){//起恢复现场的作用StringBuffer path = new StringBuffer(curPath);path.append(Integer.toString(root.val));if(root.left == null && root.right == null){ret.add(path.toString());return;}path.append("->");if(root.left != null) dfs(root.left,path);if(root.right !=null) dfs(root.right,path);}