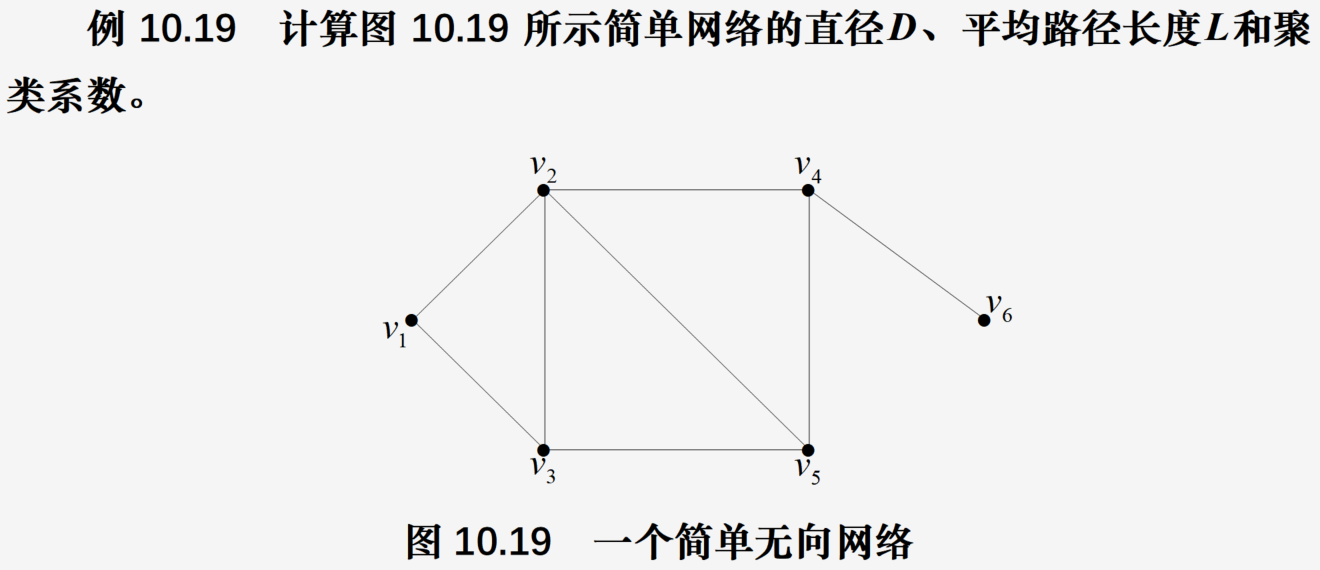
终于是学完了,这个最短路我学了好几天,当然也学了别的算法啦,也是非常的累啊。
话不多说下面看看最短路问题吧。

最短路问题是有向图,要求的是图中一个点到起点的距离,其中我们要输入点和点之间的距离,来求最短路。
下面分为几类题目:
单源汇最短路-->一个起点
1.边权为正数(dijkstra)
dijkstra算法的原理其实是拿第一个点与相连接的点进行距离上的比较,让距离最近的点作为下一个比较的第一个点,由于是边权为正数,所以不用去考虑负数和负环路。但是为啥我要分为两种类型,不是因为优化就是比朴素好,因为他们的存储数据不同,要存储的方式也是不同的,所以方法也是不同的。
方法:
dis[1]=0,dis[i]=0x3f正无穷
for(int i=1~n) 当前已经确定最短距离的点(当然用邻接表存储的for(int i=h[st];i!=-1;i=ne[i]))
t<-不在s中的距离最近的点
s<-t
用t更新其他点的距离
(1)朴素 O(n^2) n点数m边数-->边数较多-->稠密图-->邻接矩阵
看题:
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围
1≤n≤500,
1≤m≤10^5,
图中涉及边长均不超过10000。
看这个
输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3代码实现:
#include<bits/stdc++.h>
using namespace std;
const int N=510;
int n,m;
int g[N][N];
int dis[N];
bool st[N];
int Dijkstra(){memset(dis,0x3f,sizeof dis);dis[1]=0;for(int i=0;i<n;i++){int t=-1;for(int j=1;j<=n;j++)//j-x当前的点if(!st[j]&&(t==-1||dis[t]>dis[j]))t=j;// if(t==n)break;st[t]=true;for(int j=1;j<=n;j++)dis[j]=min(dis[j],dis[t]+g[t][j]);}if(dis[n]==0x3f3f3f3f)return -1;return dis[n];
}
signed main(){ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin>>n>>m;memset(g,0x3f,sizeof g);while(m--){int a,b,c;cin>>a>>b>>c;g[a][b]=min(g[a][b],c);} cout<<Dijkstra()<<endl;
}(2)堆优化版 O(mlogn)-->边少-->稀疏图-->邻接表
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为非负值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围
1≤n,m≤1.5×10^5,
图中涉及边长均不小于 0,且不超过 10000。
数据保证:如果最短路存在,则最短路的长度不超过 10^9。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3代码实现(因为是队列嘛,咱们也可以使用模拟队列):
#include<bits/stdc++.h>
#include<cstring>//memset函数的头文件
#include<iostream>
#include<algorithm>
#include<queue>
#define xx first
#define yy second
using namespace std;
const int N = 150010;
typedef pair<int, int>PII;//前者是距离 堆中按照前者距离排序 后者是点序号
priority_queue<PII, vector<PII>, greater<PII>>heap;//小根堆
int h[N], w[N], e[N], ne[N], idx;//稀疏图用邻接表储存 w[N]存权重
int dist[N];//起点点到终点的(当前)最短距离
bool vis[N];//标记起点到某个点的最短距离是否确定
int st,ed;//起点到终点
int n, m;
//数组模拟邻接表的插入函数
void add(int a, int b, int c){//存在一条从点a到点b的有向边 距离为ce[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
int Dijkstra(int st, int ed){//初始设定起点点到其他所有点距离为正无穷memset(dist, 0x3f, sizeof dist);//起点到起点距离为0 加入堆dist[st] = 0;//第一参数是距离//第二参数是终点编号heap.push({ 0,st });while (heap.size()){auto t = heap.top();heap.pop();//取出后一定要弹出int ver = t.yy, distance = t.xx;//ver取得该点的下标if (vis[ver])continue;//已经确定了就跳过//要做就先确定下来//出队时确定加入S集合vis[ver] = true;//把确定下来的那个点能拓展到的新点 加入堆for (int i = h[ver];~i;i = ne[i]){int j = e[i];if (dist[j] > distance + w[i]){dist[j] = distance + w[i];heap.push({ dist[j],j });}}}if (dist[ed] == 0x3f3f3f3f)return -1;//不连通return dist[ed];
}
int main(){memset(h, -1, sizeof h);//初始化邻接表表头scanf("%d%d", &n, &m);while (m--){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c);}printf("%d\n", Dijkstra(1, n));
}2.存在负边权
贝尔曼的原理嘛,是一个叫做三角不等式的松弛操作实现的,但是由于是双重循环把所有的边都遍历了一遍,所以时间复杂度为O(nm),而相对于下面的SPFA算法嘛,一般都比较常用spfa。
(1)Bellman-ford O(nm)

你看这个可以在1->2->3->4->2走无穷次,导致最终结果为负无穷
但是他可以走有限条边,即使是万能的spfa也不行,因为这就是遍历的一步。
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你求出从 1 号点到 n 号点的最多经过 k 条边的最短距离,如果无法从 1 号点走到 n 号点,输出 impossible。
注意:图中可能 存在负权回路 。
输入格式
第一行包含三个整数 n,m,k。
接下来 m 行,每行包含三个整数x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
点的编号为 1∼n。
输出格式
输出一个整数,表示从 1 号点到 n 号点的最多经过 k 条边的最短距离。
如果不存在满足条件的路径,则输出 impossible。
数据范围
1≤n,k≤500,
1≤m≤10000,
1≤x,y≤n,
任意边长的绝对值不超过 10000。
输入样例:
3 3 1
1 2 1
2 3 1
1 3 3
输出样例:
3代码实现:
#include<bits/stdc++.h>
#include<cstring>
#include<iomanip>
#include<iostream>
using namespace std;
const int N=510,M=1e4+10;
int n,m,k;
int dis[N],backup[N];
struct tu
{int a,b,w;
}edge[M];
void Bellman_ford(){memset(dis,0x3f,sizeof dis);dis[1]=0;for(int i=0;i<k;i++){memcpy(backup,dis,sizeof dis);for(int j=0;j<m;j++){int a=edge[j].a,b=edge[j].b,w=edge[j].w;dis[b]=min(dis[b],backup[a]+w);}}
}
int main(){scanf("%d%d%d",&n,&m,&k);for(int i=0;i<m;i++){int a,b,w;cin>>a>>b>>w;// edge[i].a=a,edge[i].b=b,edge[i].w=w;edge[i]={a,b,w};}Bellman_ford();if(dis[n]>0x3f3f3f3f/2)cout<<"impossible";else cout<<dis[n];
}(2)SPFA O(m),最坏O(nm)-->贪心
前提是:
不含负环,但是同样适用于dijkstra题目

这个算法虽然不能适用于求负环的最短路,但是他可以判断是不是含有负环,详细看注释掉的部分。
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 impossible。
数据保证不存在负权回路。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 impossible。
数据范围
1≤n,m≤10^5,
图中涉及边长绝对值均不超过 10000。
输入样例:
3 3
1 2 5
2 3 -3
1 3 4
输出样例:
2代码实现:
#include<cstring>//memset函数的头文件
#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 100010;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool vis[N];
int n, m;
// int cnt[N];
void add(int a, int b, int c){e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
int spfa(){memset(dist,0x3f,sizeof dist);dist[1]=0;queue<int> q;q.push(1);vis[1]=true;while(q.size()){int t=q.front();q.pop();vis[t]=false;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(dist[j]>dist[t]+w[i]){dist[j]=dist[t]+w[i];// cnt[j]=cnt[t]+1;// if(cnt[j]>=n)return true;//判断是不是存在负环if(!vis[j]){q.push(j);vis[j]=true;}}}}return dist[n];// return false;
}
signed main(){scanf("%d%d", &n, &m);memset(h, -1, sizeof h);while(m -- ){int a,b,c;scanf("%d%d%d",&a,&b,&c);add(a,b,c);}int t=spfa();if(t==0x3f3f3f3f) puts("impossible");else printf("%d",t);// if(spfa())puts("Yes");// else puts("No");
}多源汇最短路 Floyd O(n^3)-->dp
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,边权可能为负数。
再给定 k 个询问,每个询问包含两个整数 x 和 y,表示查询从点 x 到点 y 的最短距离,如果路径不存在,则输出 impossible。
数据保证图中不存在负权回路。
输入格式
第一行包含三个整数 n,m,k。
接下来 m 行,每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
接下来 k 行,每行包含两个整数 x,y,表示询问点 x 到点 y 的最短距离。
输出格式
共 k 行,每行输出一个整数,表示询问的结果,若询问两点间不存在路径,则输出 impossible。
数据范围
1≤n≤200,
1≤k≤n2
1≤m≤20000,
图中涉及边长绝对值均不超过 10000。
输入样例:
3 3 2
1 2 1
2 3 2
1 3 1
2 1
1 3
输出样例:
impossible
1代码实现:
#include<iostream>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;
const int N=200+10,INF=1e9;
int m,n,Q;
int d[N][N];
void floyd(){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){for(int k=1;k<=n;k++){d[i][j]=min(d[i][j],d[i][k]+d[k][j]);}}}
}signed main(){scanf("%d%d%d",&n,&m,&Q);//initfor(int i=1;i<=n;i++)for(int j=1;j<=n;j++)if(i==j)d[i][j]=0;else d[i][j]=INF;//inputwhile(m--){int a,b,c;scanf("%d%d%d",&a,&b,&c);d[a][b]=min(d[a][b],c);}floyd();while(Q--){int a,b;scanf("%d%d",&a,&b);if(d[a][b]>INF/2)puts("impossible");elseprintf("%d",d[a][b]);}
}
以上就是求最短路的所有方法啦。