1.什么是位置编码
位置编码描述序列中实体的位置或位置,以便为每个位置分配唯一的表示形式。单个数字(如索引值)不用于表示项目在转换器模型中的位置的原因有很多。对于长序列,索引的量级可能会变大。如果将索引值归一化为介于 0 和 1 之间,则可能会对可变长度序列产生问题,因为它们的归一化方式会有所不同。
转换器使用智能位置编码方案,其中每个位置/索引都映射到一个向量。因此,位置编码层的输出是一个矩阵,其中矩阵的每一行表示序列的一个编码对象,该序列与其位置信息相加。仅对位置信息进行编码的矩阵示例如下图所示。
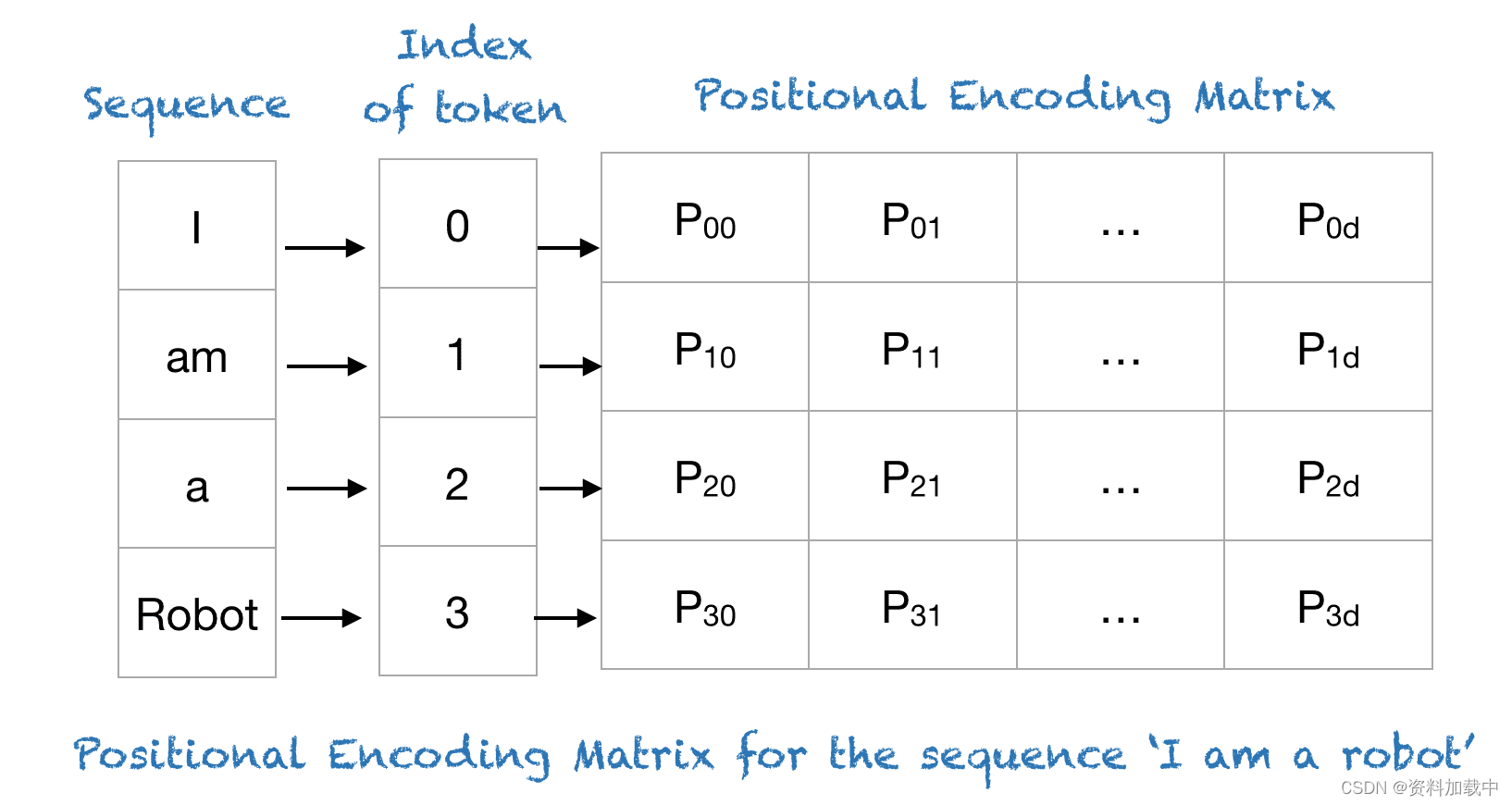
2.位置编码的原理
三角正弦函数的回顾
函数的范围是 [-1,+1]。该波形的频率是在一秒钟内完成的周期数。波长是波形重复的距离。不同波形的波长和频率如下所示:
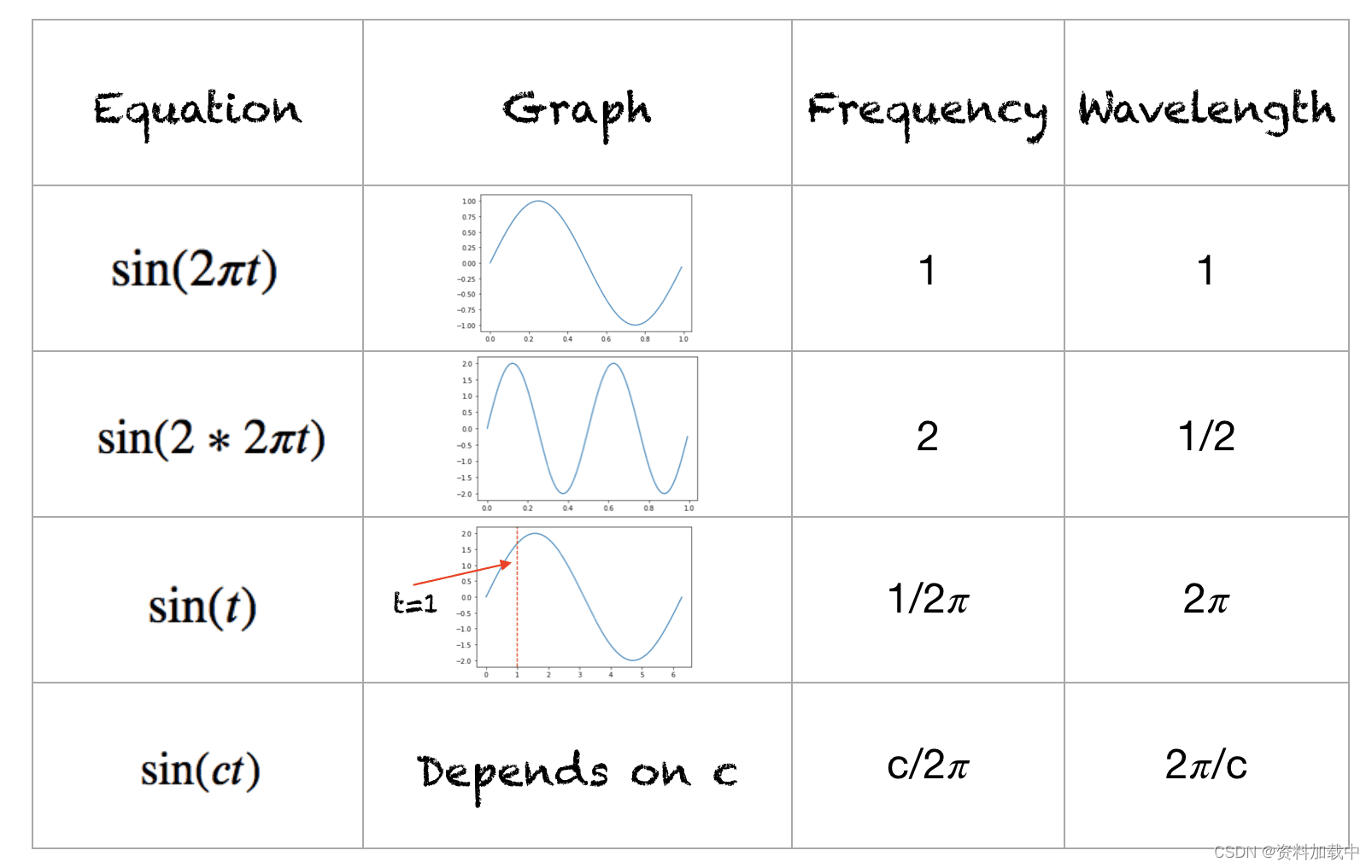
Transformer中的位置编码
假设您有一个长度 L 的输入序列,并且需要 对象在此序列中的位置。位置编码由不同频率的正弦和余弦函数给出:
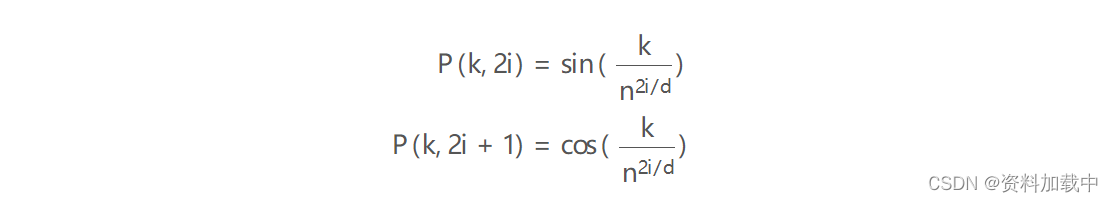
- k:对象在输入序列中的位置,0<=k<L/2
- d: 输出嵌入空间的维度
- P(k,j): 位置函数,用于映射输入序列中k处的元素到位置矩阵的(k,j)处
- n:用户定义的标量,由 Attention Is All You Need 的作者设置为 10,000。
- i: 用于映射到列索引,0<=i<d/2,单个值i映射到正弦和余弦函数
为了理解上面的表达式,让我们以 n=100 和 d=4 的短语“I am a robot”为例。 下表显示了该短语的位置编码矩阵。 事实上,位置编码矩阵对于任何 n=100 和 d=4 的四字母短语都是相同的。

3.代码实现位置编码矩阵
import numpy as np
import matplotlib.pyplot as pltdef getPositionEncoding(seq_len, d, n=10000):P = np.zeros((seq_len, d))for k in range(seq_len):for i in np.arange(int(d/2)):denominator = np.power(n, 2*i/d)P[k, 2*i] = np.sin(k/denominator)P[k, 2*i+1] = np.cos(k/denominator)return PP = getPositionEncoding(seq_len=4, d=4, n=100)
print(P)结果
[[ 0. 1. 0. 1. ][ 0.84147098 0.54030231 0.09983342 0.99500417][ 0.90929743 -0.41614684 0.19866933 0.98006658][ 0.14112001 -0.9899925 0.29552021 0.95533649]]4.理解并可视化位置编码矩阵
要理解位置编码,让我们从查看 n=10,000 和 d=512 的不同位置的正弦波开始。
def plotSinusoid(k, d=512, n=10000):x = np.arange(0, 100, 1)denominator = np.power(n, 2*x/d)y = np.sin(k/denominator)plt.plot(x, y)plt.title('k = ' + str(k))fig = plt.figure(figsize=(15, 4))
for i in range(4):plt.subplot(141 + i)plotSinusoid(i*4)下图是上面代码的输出:
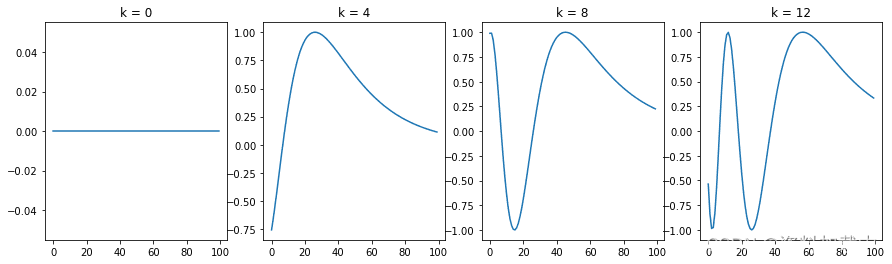
可以看到每个位置对应于不同的正弦曲线,它将单个位置编码为向量。 如果仔细观察位置编码函数,你会发现固定i时对应的波长:
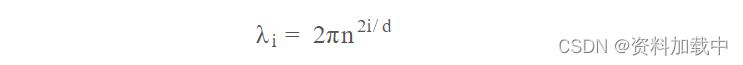
因此,正弦曲线的波长形成几何级数。并且从2Π到2Πn变化, 位置编码方案具有许多优点。
- 正弦和余弦函数的值在 [-1, 1] 内,这使位置编码矩阵的值保持在归一化范围内。
- 由于每个位置的正弦曲线都不同,因此你可以采用独特的方式对每个位置进行编码。
- 有一种方法可以测量或量化不同位置之间的相似性,从而使你能够对单词的相对位置进行编码。
可视化位置矩阵
让我们在更大的值上可视化位置矩阵。使用库中的 matplotlib Python matshow() 方法。按照原始论文中所做的设置 n=10,000,您将得到以下内容:
P = getPositionEncoding(seq_len=100, d=512, n=10000)
cax = plt.matshow(P)
plt.gcf().colorbar(cax)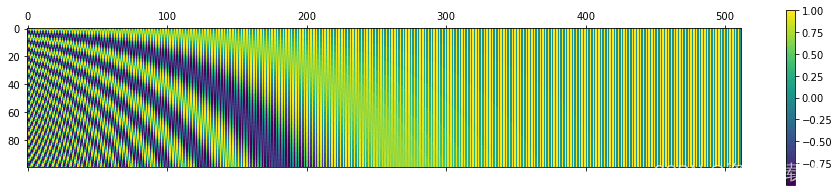
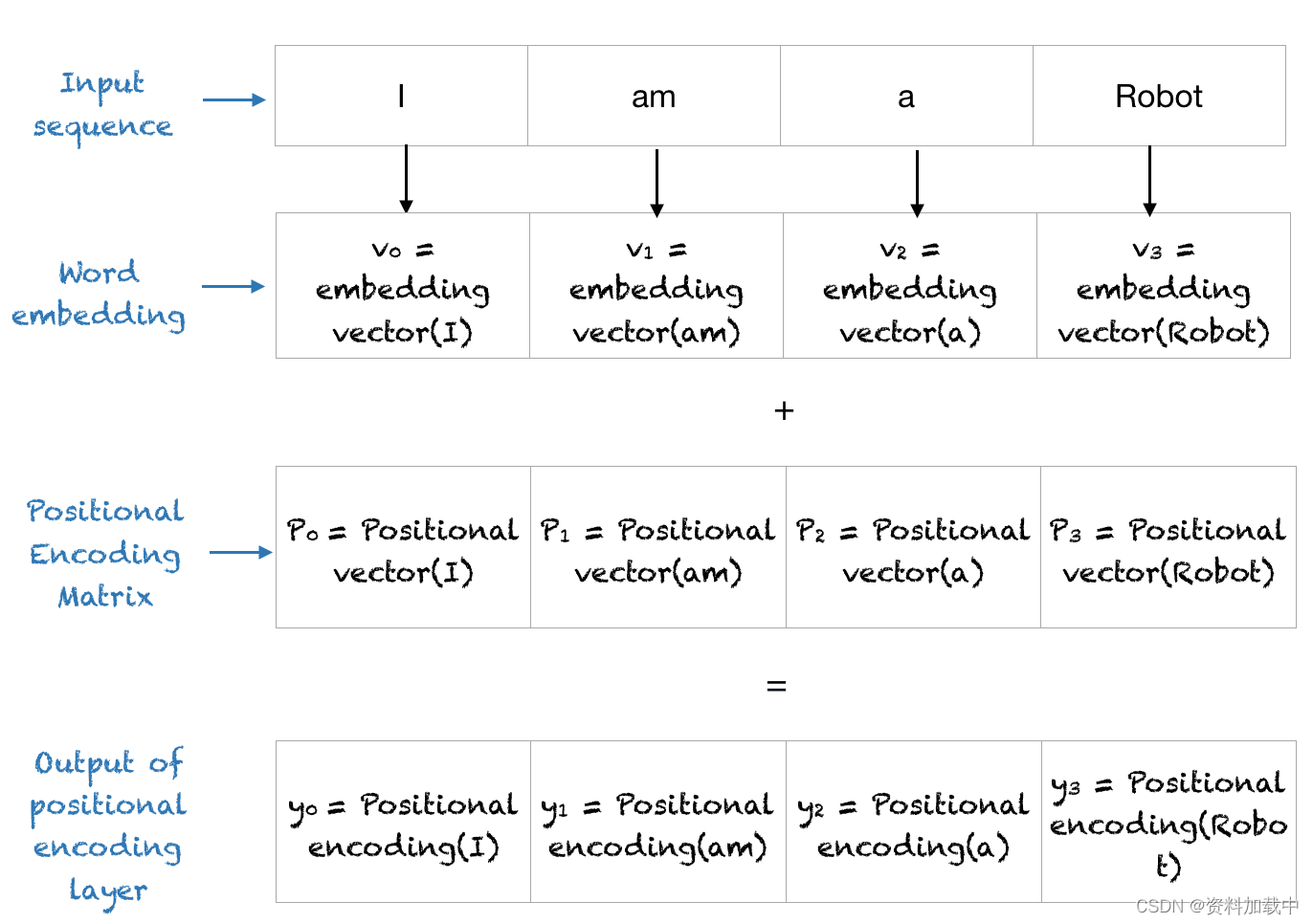
位置编码层将位置向量与单词编码相加,并为后续层输出此矩阵。整个过程如下所示。
参考链接
A Gentle Introduction to Positional Encoding in Transformer Models, Part 1 - MachineLearningMastery.com