【定理】
1. 无穷小量 * 有界 == 无穷小量
简单理解为:0 乘以任何数都等于 0 ,因为常数 0 是无穷小量
2. 设 lim f(x)== a , lim g (x) == b
加减:lim[f(x) ± g(x) ] == lim f(x) ± g(x) == a ± b
乘:lim[f(x) * g(x) ] == lim f(x) * g(x) == a * b
除(b ≠ 0):lim[f(x) / g(x) ] == lim f(x) / g(x) == a / b
数乘:lim[c * f(x)] == c * limf(x)
幂运算:lim[f(x)的n次方] == [limf(x)] 的n次方 == a 的n 次方
幂指运算:lim[f(x) 的 g(x)次方] == [limf(x)] 的 limg(x) 次方
极限的运算法则【高数笔记】
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.rhkb.cn/news/249365.html
如若内容造成侵权/违法违规/事实不符,请联系长河编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
Spring Bean 定义常见错误
Spring 的核心是围绕 Bean 进行的。不管是 Spring Boot 还是 Spring Cloud,只要名称中带有 Spring 关键字的技术都脱离不了 Bean,而要使用一个 Bean 少不了要先定义出来,所以定义一个 Bean 就变得格外重要了。
当然,对于这么重要…
【深入浅出SpringCloud原理及实战】「Netflix系列之Hystrix」针对于限流熔断组件Hystrix的回退降级实现方案和机制
针对于限流熔断组件Hystrix的回退降级实现方案和机制 依赖隔离依赖隔离之线程&线程池高延迟请求的例子 线程池的优势线程池的弊端线程池的开销线程池开销 信号量 依赖隔离 Hystrix通过使用『舱壁模式』(注:将船的底部划分成一个个的舱室,…
186205-33-4,Cyanine2 NHS Ester,广泛应用于荧光标记和生物成像领域
您好,欢迎来到新研之家
文章关键词:186205-33-4,Cyanine2 NHS Ester,Cy2 NHS,Cyanine2 NHS Ester,Cy2 NHS
一、基本信息
产品简介:Cyanine2 NHS Ester can be widely used in the fields of …
C#中的WebApi响应Accept头,自动返回xml或者json
Global.asax.cs中的Application_Start方法添加
GlobalConfiguration.Configuration.Formatters.Clear(); GlobalConfiguration.Configuration.Formatters.Add(new XmlMediaTypeFormatter()); GlobalConfiguration.Configuration.Formatters.Add(new JsonMediaTypeFormatter())…
【零基础学习CAPL】——CAN报文的发送(按下按钮同时周期性发送)
🙋♂️【零基础学习CAPL】系列💁♂️点击跳转 文章目录 1.概述2.面板创建3.系统变量创建4.CAPL实现4.1.函数展示4.2.全量报文展示5.效果1.概述
本章主要介绍使用CAPL和Panel在按下按钮时发送周期性CAN报文。 本章主要在“【零基础学习CAPL】——CAN报文的发送(配合P…
MQ面试题之Kafka
前言
前文介绍了消息队列相关知识,并未针对某个具体的产品,所以略显抽象。本人毕业到现在使用的都是公司内部产品,对于通用产品无实际经验,但是各种消息中间件大差不差,故而本次选择一个相对较熟悉的Kafka进行详细介绍…
Spring的事件监听机制
这里写自定义目录标题 1. 概述(重点)2. ApplicationEventMulticaster2.1 SimpleApplicationEventMulticaster2.2 AbstractApplicationEventMulticaster 3. ApplicationListener3.1 注册监听器3.2 自定义 4. SpringApplicationRunListeners 1. 概述&#…
【软件设计师笔记】计算机系统基础知识考点
🐓 计算机系统组成
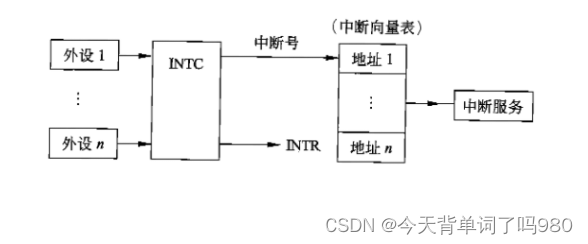
计算机系统是由硬件和软件组成的,它们协同工作来运行程序。计算机的基本硬件系统由 运算器、控制器、存储器、输入设备和输出设备5大部件组成。运算器、控制器等部件被集成 在一起统称为中央处理单元(Central Processing …
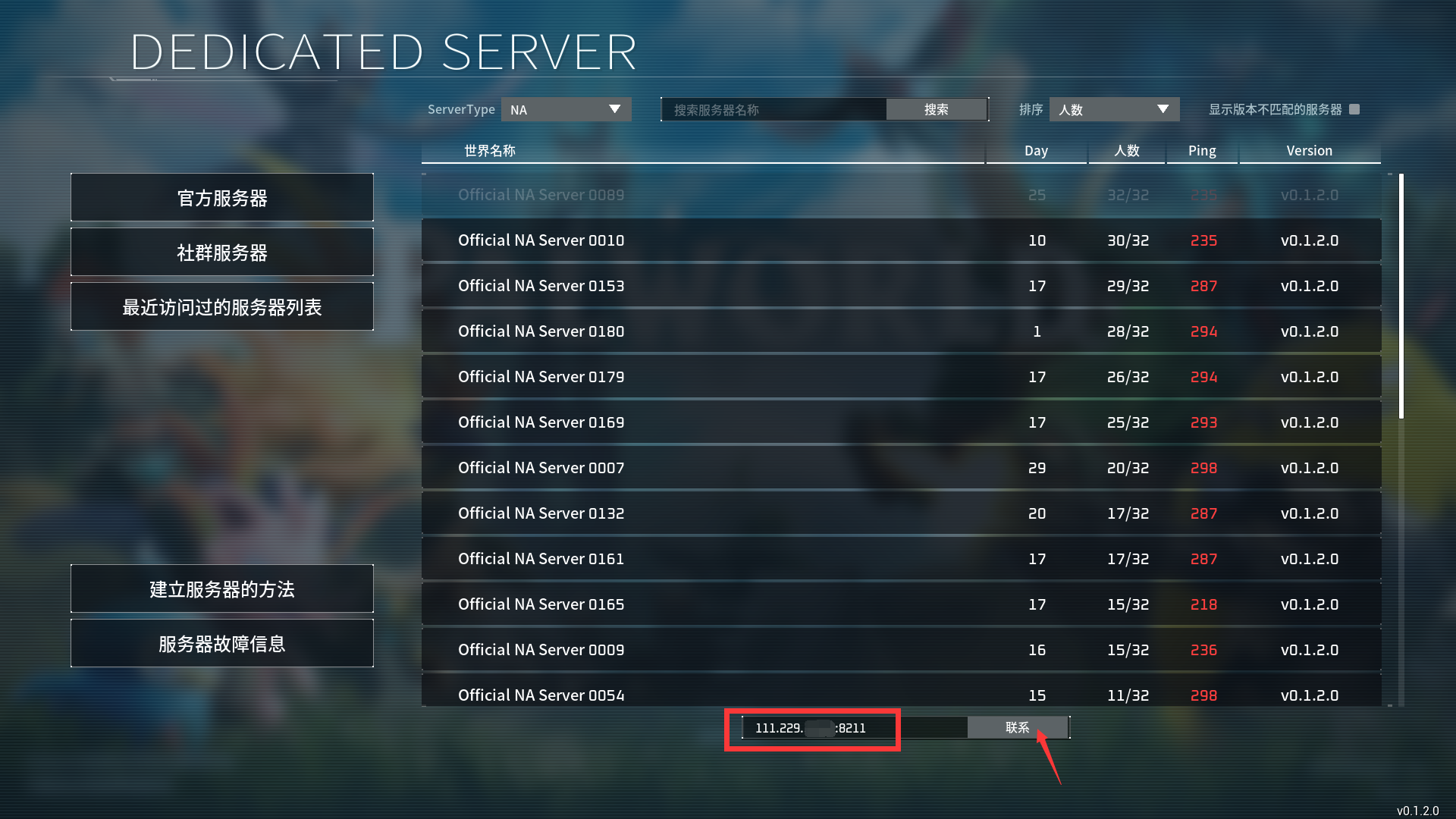
小白级教程,10秒开服《幻兽帕鲁》
在帕鲁的世界,你可以选择与神奇的生物「帕鲁」一同享受悠闲的生活,也可以投身于与偷猎者进行生死搏斗的冒险。帕鲁可以进行战斗、繁殖、协助你做农活,也可以为你在工厂工作。你也可以将它们进行售卖,或肢解后食用。 前言
马上过年…
MFC串行化的应用实例
之前写过一篇MFC串行化的博文;下面看一个具体例子;
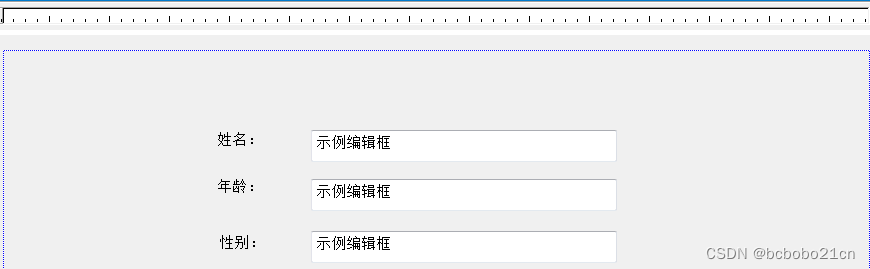
新建一个单文档应用程序;在最后一步,把View类的基类改为CFormView; 然后在资源面板编辑自己的字段; 然后到doc类的头文件添加对应变量,
public:CString name;int age;CString sex;CString dept;CString zhiwu;CStrin…
go语言socket编程
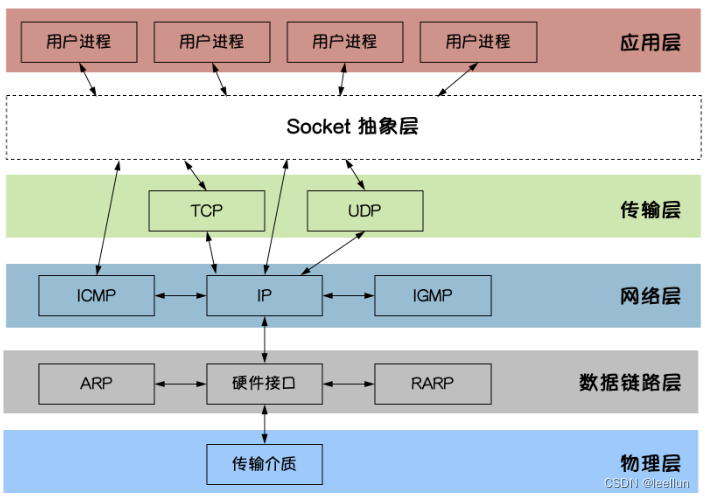
1.互联网分层模型 过程分析: 2.Socket图解
Socket是应用层与TCP/IP协议族通信的中间软件抽象层。在设计模式中,Socket其实就是一个门面模式,它把复杂的TCP/IP协议族隐藏在Socket后面,对用户来说只需要调用Socket规定的相关函数&a…
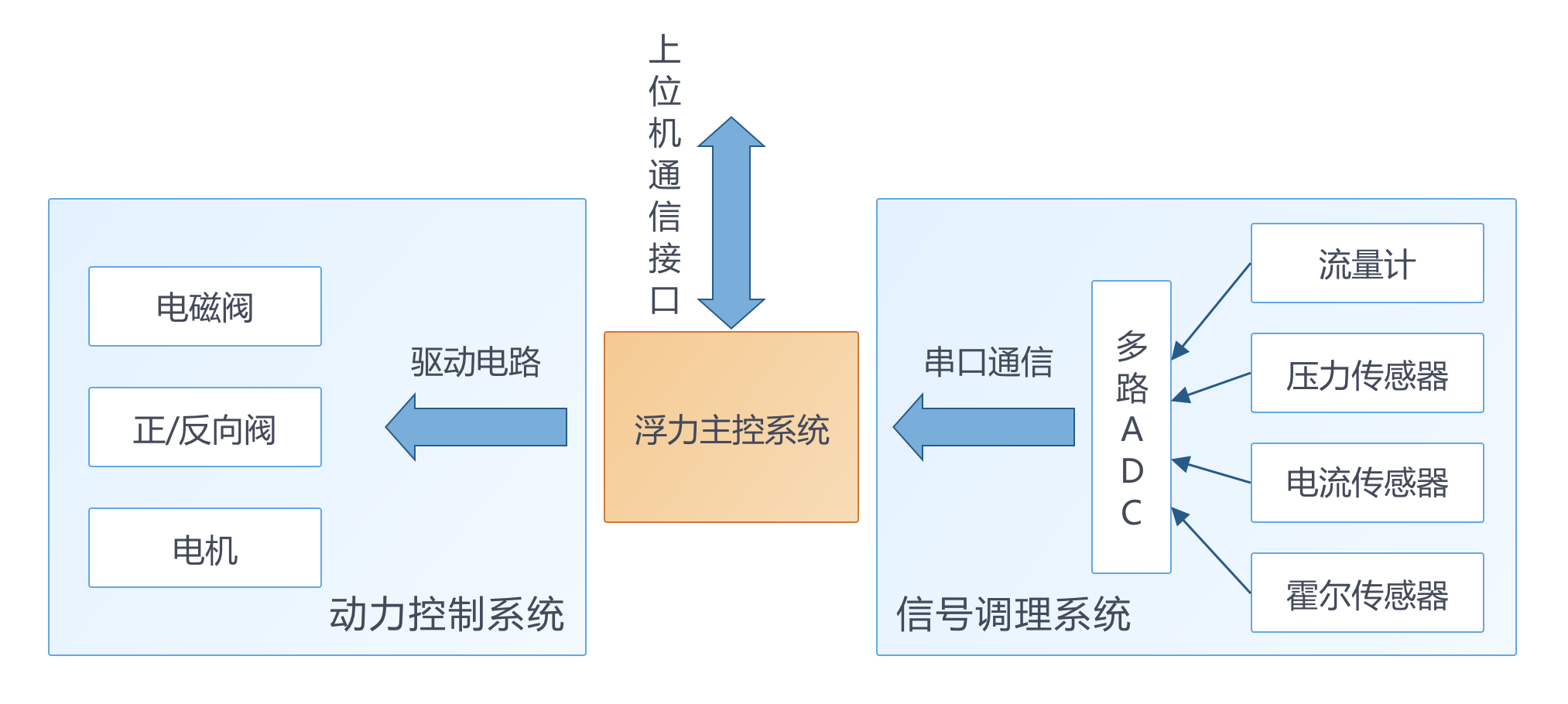
助力水下潜行:浮力调节系统仿真
01.建设海洋强国
海洋蕴藏着丰富的资源,二十大报告强调,要“发展海洋经济,保护海洋生态环境,加快建设海洋强国”。建设海洋强国旨在通过科技创新驱动、合理开发利用海洋资源、强化海洋环境保护与生态修复、提升海洋经济质量等多个…
测试access和trunk口的区别(华为)
思科设备参考:测试access和trunk口的区别(思科)
一,实验目的
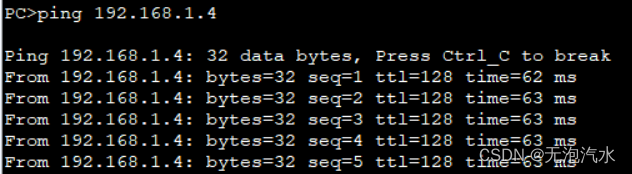
实现同一 Vlan 内的主机互通,不同 Vlan 间的主机隔离。 二,配置前测试
PC1分别ping PC2、PC3、PC4都能通,因为四台PC默认同处于v…
AOP+Redisson 延时队列,实现缓存延时双删策略
一、缓存延时双删
关于缓存和数据库中的数据保持一致有很多种方案,但不管是单独在修改数据库之前,还是之后去删除缓存都会有一定的风险导致数据不一致。而延迟双删是一种相对简单并且收益比较高的实现最终一致性的方式,即在删除缓存之后&…
强化学习原理python篇07——策略梯度法
强化学习原理python篇07——策略梯度法 Average state valueAverage rewardMonte Carlo policy gradient (REINFORCE)REINFORCE示例在torch里面编写这段代码1、用随机权重初始化策略网络2、运行N个完整的片段,保存其(s,a,r,s)状态转移3、对于每个片段k的每一步t&…
Web中的转发与重定向
转发与重定向 一、转发和重定向的概念1.转发2.重定向 二、JavaWeb 中的转发和重定向三、SpringMVC 中的转发和重定向1.转发(1) 默认的方式(2) 完整的方式 2.重定向 四、总结 一、转发和重定向的概念
在 Web 应用中,转发和重定向都是用于将请求从一个页面传递到另一…
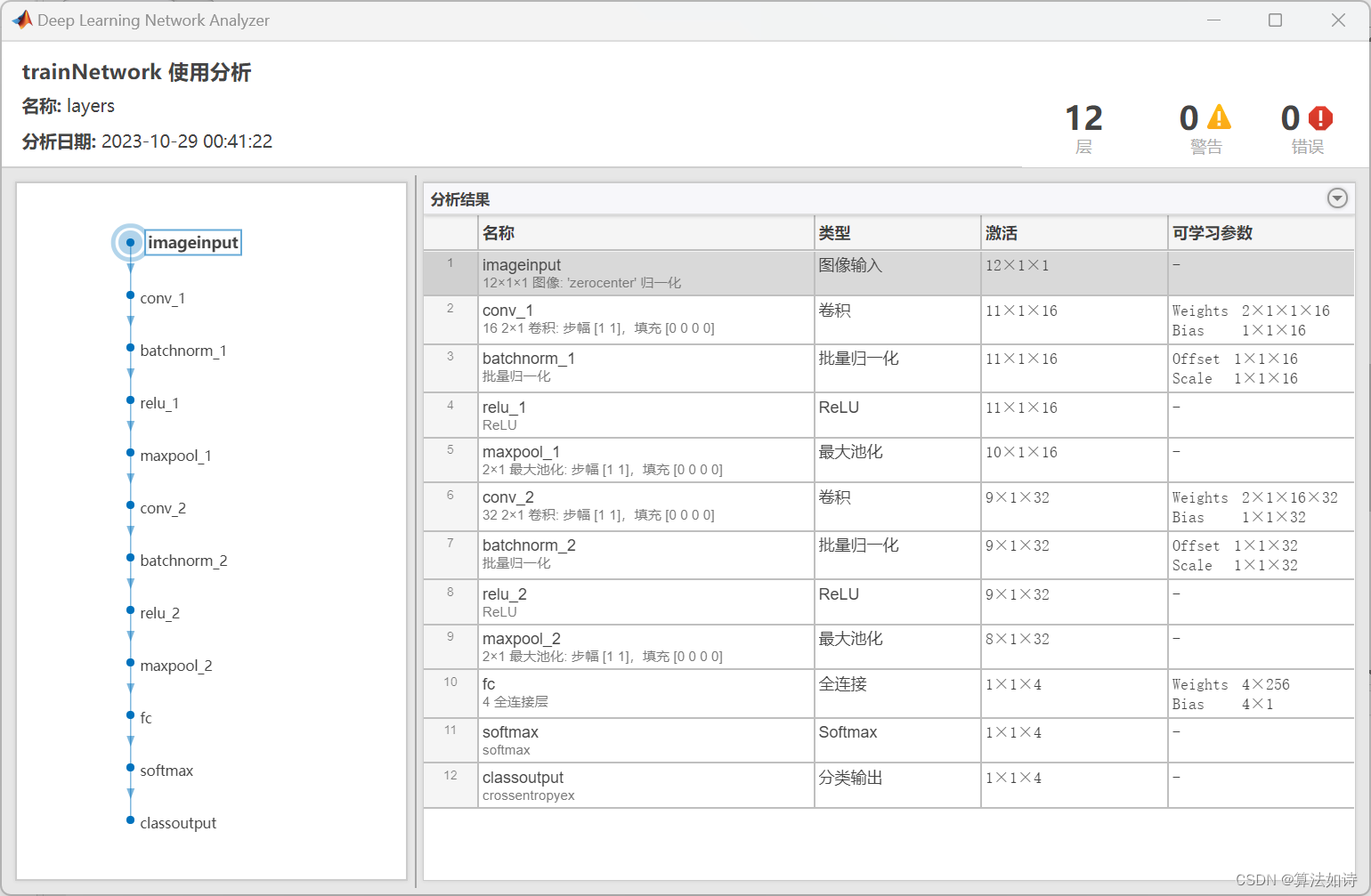
故障诊断 | 一文解决,CNN卷积神经网络故障诊断(Matlab)
文章目录 效果一览文章概述专栏介绍源码设计参考资料效果一览 文章概述 故障诊断 | 一文解决,CNN卷积神经网络故障诊断(Matlab) 专栏介绍 订阅【故障诊断】专栏,不定期更新机器学习和深度学习在故障诊断中的应用;订阅
外星人入侵(python)
前言
代码来源《python编程从入门到实践》Eric Matthes 署 袁国忠 译
使用软件:PyCharm Community Editor 2022
目的:记录一下按照书上敲的代码 alien_invasion.py
游戏的一些初始化设置,调用已经封装好的函数方法,一个函数的…
【React】前端项目引入阿里图标
【React】前端项目引入阿里图标 方式11、登录自己的iconfont-阿里巴巴矢量图标库,把需要的图标加入到自己的项目中去;2、加入并进入到项目中去选择Font class 并下载到本地3、得到的文件夹如下4. 把红框中的部分粘贴到自己的项目中(public 文…
推荐文章