数据结构-内部排序

简介

排序（Sorting）：将一个数据元素（或记录）的任意序列，重新排列成一个按关键字有序的序列

排序算法分为内部排序和外部排序

内部排序：在排序期间数据对象全部存放在内存的排序

外部排序：在排序期间全部对象个数太多，不能同时存放在内存，必须根据排序过程的要求，不断在内、外存之间移动的排序

排序方法的稳定性：

如果在记录序列中有两个记录r[i]和r[j], 它们的关键字key[i]==key[j]且在排序之前, 记录r[i]排在r[j]前面。

如果在排序之后, 记录r[i]仍在记录r[j]的前面, 则称这个排序方法是稳定的, 否则称这个排序方法是不稳定的

排序常用的数据结构是数组、顺序表、结构体

排序算法的应用非常广泛，商业领域、生活领域、科研领域都几乎离不开排序

淘宝商品价格排序（海量数据排序）

微博热搜排行榜（点击量动态排序）

QQ好友列表（字符排序）

数列相似度（将数列元素排序后对比）

元素唯一性（排序后找出重复项）

凸包问题（例如图像识别手势，采点绘制轮廓）

排序介绍

排序包含两种基本操作

比较：比较两个关键字的大小

移动：将记录从一个位置移动至另一个位置

排序算法的时间复杂度，用算法执行中的记录关键字比较次数与记录移动次数来衡量

根据排序思想来划分，内部排序算法分为五类

插入排序：直接插入排序、希尔排序

交换排序：冒泡排序、快速排序

选择排序：简单选择排序、堆排序

归并排序：两路归并排序

基数排序：k进制位数排序

判断排序好坏的方法

算法的时间复杂度、空间复杂度

算法的稳定性

排序算法的最好情况（比较和移动次数最少）

排序算法的最坏情况（比较和移动次数最多）

初始待排序序列是否会影响排序算法性能

排序次数是否固定

每一趟排序能否确定一个元素的最终排序位置

插入排序

插入排序的思想：假设前k-1个记录已经排序，第k个元素找到合适位置插入。分为

直接插入排序

希尔排序

直接插入排序

1. 直接插入排序是最简单的排序方法，操作：

每步将一个待排序的对象,按其关键字大小,插入到前面已经排好序的有序表的适当位置上, 直到对象全部插入为止

2. 直接插入排序的算法步骤：

当插入第i(i≥1)个对象时, 前面的r[0], r[1], …, r[i-1]已经排好序。

用r[i]的关键字与r[i-1], r[i-2], …的关键字顺序进行比较(和顺序查找类似)，如果小于，则将r[x]向后移动(插入位置后的记录向后顺移)

找到插入位置即将r[i]插入

3. 直接插入排序的算法分析

直接插入排序的时间复杂度为O(n2)，空间复杂度O(1)

直接插入排序是一种稳定的排序方法

直接插入排序最大的优点是简单，在记录数较少时，是比较好的办法

4.其他

算法性能与关键字的初始排列有关，成正比关系。初始排列越有序，比较和移动次数越少

最好情况，排序前已经有序，总比较次数n-1，移动次数0

最坏情况，排序前是逆序，每趟排序都要比较i-1次和移动i-1次，总比较次数n2/2，总移动次数n2/2

每趟排序不能确定一个元素的最终排序位置，例如最后一个元素是最小值插入到第一个元素位置，导致前n-1个元素都要后移

//直插排序
/*
因为直接插入排序过程中，前i-1个元素是有序的，所以可以改进为折半插入排序
折半插入排序是指在查找记录插入位置时，采用折半查找算法，折半查找比顺序查找快，所以折半插入排序在查找上性能比直接插入排序好
由于需要移动的记录数目与直接插入排序相同(为O(n2))，所以折半插入排序的时间复杂度为O(n2)
*/
void insert(int *a)
{for(int i=1;i<l;i++){int tmp=a[i];int j=i;while(j>0){if(a[j-1]<tmp)break;a[j]=a[j-1];j--;}a[j]=tmp;}
}

希尔排序

1.希尔排序的思想：先将待排序列分成若干子序列；对其分别进行插入排序；待整个序列基本有序时，再对全体记录进行一次直接插入排序，希尔排序（Shell Sort）又称为缩小增量排序

2. 希尔排序的算法设计

首先取一个整数 gap < n(待排序记录数) 作为间隔, 将全部记录分为 gap 个子序列, 所有距离为 gap 的记录放在同一个子序列中

在每一个子序列中分别施行直接插入排序。

然后缩小间隔 gap, 例如取 gap = gap/2

重复上述的子序列划分和排序工作，直到最后取gap = 1, 将所有记录放在同一个序列中排序为止。

3. 排序举例

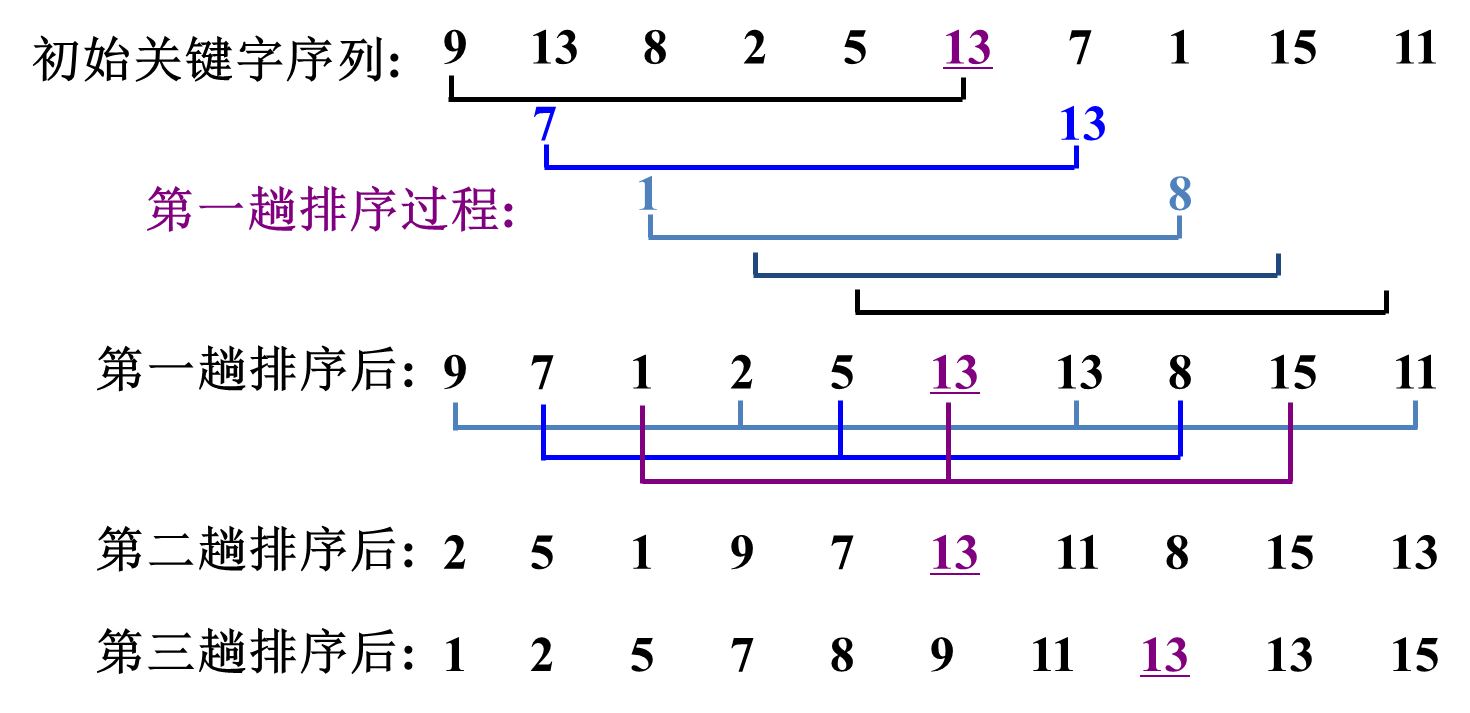
4. 希尔排序的算法分析

开始时，gap的值较大，子序列中的记录较少，排序速度较快

随着排序进展，gap值逐渐变小，子序列中记录个数逐渐变多，由于前面大多数记录已基本有序, 所以排序速度仍然很快。

gap的取法有多种，一般取法：gap=n/2，gap=gap/2，直到gap = 1

代码实现

//希尔排序
/*
希尔排序的算法分析
希尔排序所需的比较次数和移动次数约为n1.3
当n趋于无穷时可减少到n×(log2n)2
希尔排序的时间复杂度约为O(n(log2n)2)
希尔排序是一种不稳定的排序方法
*/
void Xier(int *a)
{int gap = l / 2;while (gap >=1) {for (int i = 0; i <l-gap; i++) {for (int j = i; j  < l; j += gap) {if (a[i] > a[j ])swap(a[i], a[j]);}}gap /= 2;show(a);}
}

交换排序

交换排序的思想：比较序列中前后两个位置的元素，如果符合前小后大或前大后小，则继续比较；如果不符合则交换两个位置的元素，再继续比较。

交换排序的算法有：起泡排序快速排序

起泡排序

1. 起泡排序，又称冒泡排序，算法思想：

设待排序记录序列中的记录个数为n

一般地，第i趟排序从1到n-i+1

依次比较相邻两个记录的关键字，如果发生逆序，则交换之

其结果是这n-i+1个记录中，关键字最大的记录被交换到第n-i+1的位置上，最多作n-1趟。

2. 冒泡排序的算法过程

i=1，为第一趟排序，关键字最大的记录将被交换到最后一个位置

i=2，为第二趟排序，关键字次大的记录将被交换到最后第二个位置

依此类推……

关键字小的记录不断上浮(起泡)，关键字大的记录不断下沉(每趟排序最大的一直沉到底)

3.冒泡排序举例

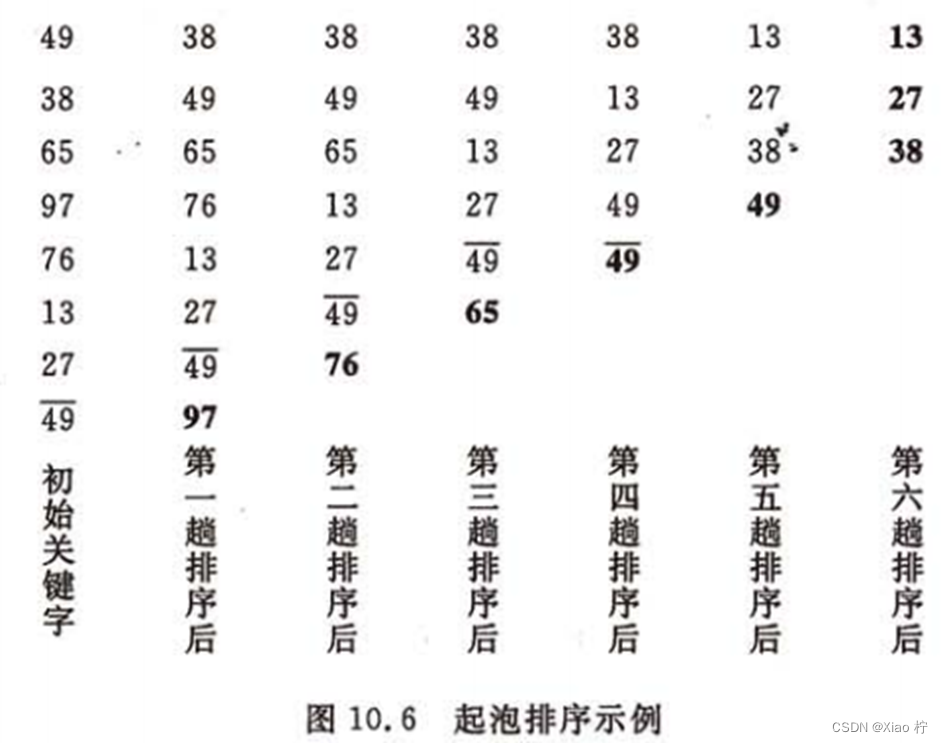
4. 冒泡排序的算法分析

起泡排序的时间复杂度为O(n2)，空间复杂度O(1)

起泡排序是一种稳定的排序方法

5. 冒泡排序的其他分析

算法性能与关键字的初始排列有关，成正比关系。初始排列越有序，比较和移动次数越少

最好情况，排序前已经有序，只执行一趟，总比较次数n-1，移动次数0

最坏情况，排序前是逆序，每趟排序都要比较i-1次和移动i-1次，总比较次数n2/2，总移动次数n2/2

冒泡排序能够提前结束，最好情况下只要一趟比较就结束。

每趟排序能够确定一个元素的最终排序位置，因为每一趟排序会把最大或最小元素排到末尾，不再参与排序

代码实现

//冒泡排序
void maopao(int *a)
{for (int i = 0; i <l; i++) {for (int j = 0; j < l - i-1; j++) {if (a[j] >= a[j + 1]) {swap(a[j], a[j + 1]);}}}
}

快速排序

1.快速排序算法设计：

任取待排序记录序列中的某个记录(例如取第一个记录)作为基准(枢),按照该记录的关键字大小,将整个记录序列划分为左右两个子序列：

左侧子序列中所有记录的关键字都小于或等于基准记录的关键字

右侧子序列中所有记录的关键字都大于基准记录的关键字

基准记录则排在这两个子序列中间(这也是该记录最终应安放的位置)

然后分别对这两个子序列重复施行上述方法，直到所有的记录都排在相应位置上为止。

基准记录也称为枢轴（或支点）记录。

2. 快速排序算法过程

取序列第一个记录为枢轴记录，其关键字为Pivotkey

指针low指向序列第一个记录位置

指针high指向序列最后一个记录位置

一趟排序(某个子序列)过程

①.从high指向的记录开始,向前找到第一个关键字的值小于Pivotkey的记录,将其放到low指向的位置,low+1

②.从low指向的记录开始,向后找到第一个关键字的值大于Pivotkey的记录,将其放到high指向的位置,high-1

③.重复1,2，直到low=high，将枢轴记录放在low(high)指向的位置

对枢轴记录前后两个子序列执行相同的操作，直到每个子序列都只有一个记录为止

3. 快速排序的算法分析

快速排序是一个递归过程, 其递归树如图所示，利用序列第一个记录作为基准，将整个序列划分为左右两个子序列。只要是关键字小于基准记录关键字的记录都移到序列左侧

可证明快速排序的平均计算时间是O(nlog2n)

实验结果表明: 就平均计算时间而言, 快速排序是所有内排序方法中最好的一个

但快速排序是一种不稳定的排序方法

代码实现

//快速排序
int getpiot(int *a, int l, int r) {int tmp = a[l];while (l < r) {while (l < r && a[r] >= tmp)r--;swap(a[r], a[l]);while (l < r && a[l] <= tmp)l++;swap(a[l], a[r]);}return l;
}
void quick_sort(int *a,int l,int r)
{if(l>=r)return;int p= getpiot(a,l,r);show(a);quick_sort(a,l,p-1);quick_sort(a,p+1,r);
}

选择排序

选择排序的思想，每一趟选出第i小(大)的元素，与第i个位置的元素交换

选择排序算法包括

简单选择排序

堆排序

简单选择排序

1.简单选择排序的算法设计：

每一趟(例如第i趟,i=1,2,…,n-1)在后面 n-i+1个待排序记录中通过n-i次比较，选出关键字最小的记录,与第i个记录交换

2.简单选择排序的算法分析

时间复杂度O(n2)

是一种不稳定的排序方法

3.其他

简单选择排序的其他分析

简单选择排序性能与记录的初始排列无关。无论是否有序，都要每趟全部扫描找出第i小(大)的元素，第i趟选择的比较次数总是 n-i次

每趟排序能够确定一个元素的最终排序位置，因为每一趟排序后，第i小(大)的元素放在第i个位置

当不需要全部排序，只需要排序出前k个元素，用简单选择排序是一种好的算法。

代码实现

//简单选择排序
void choose(int *a)
{for(int i=0;i<l-1;i++) {int mini = i;for (int j = i + 1; j < l; j++) {if (a[j] < a[mini]) {mini = j;}}if (mini != i)swap(a[i], a[mini]);}
}

堆排序

1. 堆排序算法流程

将初始序列从1至n按顺序创建一个完全二叉树

将完全二叉树调整为堆

最后结点与根结点交换

排除掉最后结点，重复步骤2，直到剩下一个结点

2. 堆排序的算法分析

对长度为n的序列，排序最多需要做n-1次调整建新堆(筛选)。建初始堆时，需要n/2次筛选，因此共需要O(n×k)量级的时间

k=log2n，堆排序时间复杂度为O(nlog2n)

堆排序是一个不稳定的排序方法

代码实现

void HeapAdjust(int* arr, int start, int end)
{int tmp = arr[start];for (int i = 2 * start + 1; i <= end; i = i * 2 + 1){if (i < end&& arr[i] < arr[i + 1])//有右孩子并且左孩子小于右孩子{i++;}//i一定是左右孩子的最大值if (arr[i] > tmp){arr[start] = arr[i];start = i;}else{break;}}arr[start] = tmp;
}
void HeapSort(int* arr)
{//第一次建立大根堆，从后往前依次调整for(int i=(l-1-1)/2;i>=0;i--){HeapAdjust(arr, i, l - 1);}show(arr);//每次将根和待排序的最后一次交换，然后在调整int tmp;for (int i = 0; i < l- 1; i++){tmp = arr[0];arr[0] = arr[l - 1-i];arr[l - 1 - i] = tmp;HeapAdjust(arr, 0, l - 1-i- 1);show(arr);}
}

归并排序

1. 归并排序的思想：将两个或两个以上的有序表合并成一个新的有序表。

两个有序顺序表合并为新的有序表时，借助多一倍空间，使得记录无需移动，直接插入新空间中。

两路归并：将初始序列分成前后两组，通过比较归并到目标序列中

2. 2路归并排序算法设计：

将n个记录看成是n个有序序列

将前后相邻的两个有序序列归并为一个有序序列(两路归并)

重复做两路归并操作，直到只有一个有序序列为止

3. 2路归并排序算法举例

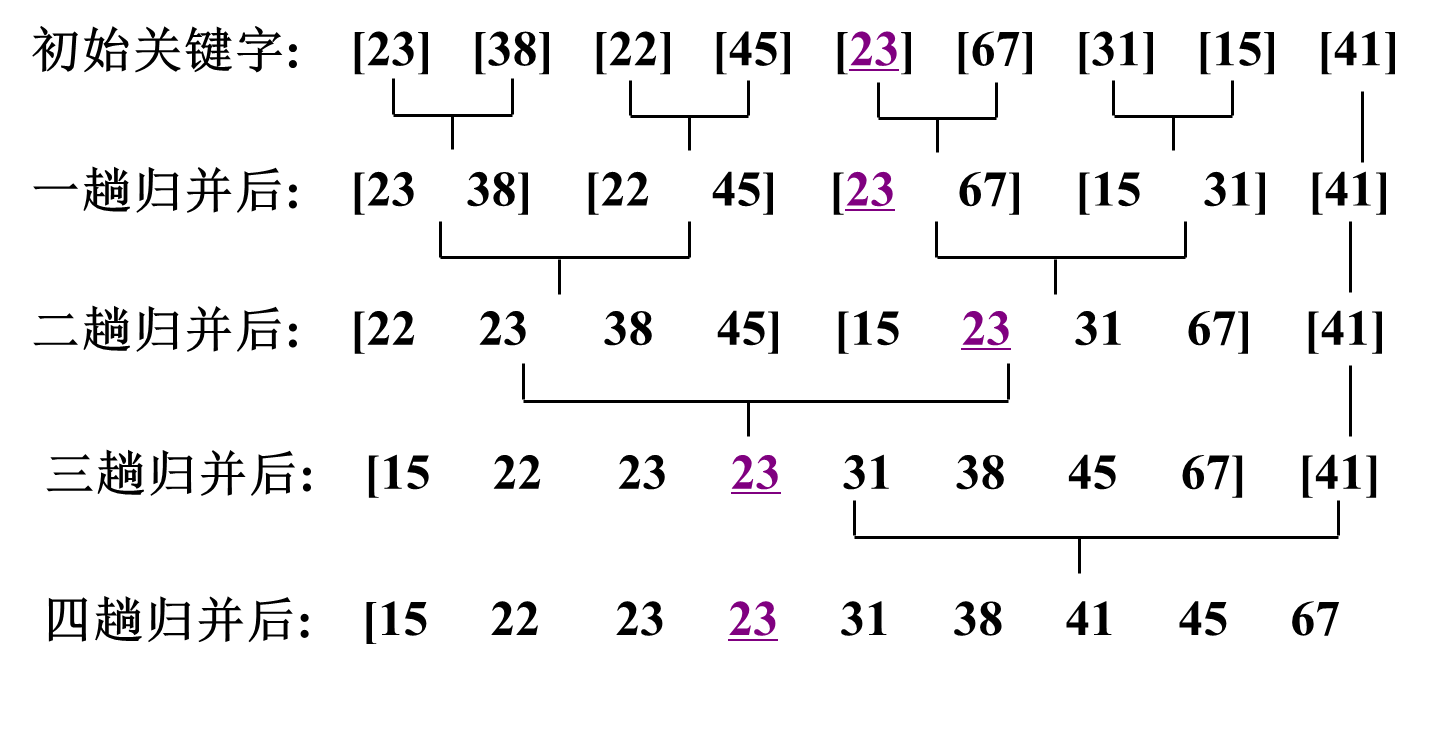
4. 2路归并排序算法分析：

如果待排序的记录为n个，则需要做log2n趟两路归并排序，每趟两路归并排序的时间复杂度为O(n)

2路归并排序的时间复杂度为O(nlog2n)

归并排序的空间复杂度是O(n)

归并排序是一种稳定的排序方法

5. 其他

归并排序优点：时间复杂度为O(nlog2n)且是稳定的排序方法

缺点需要额外空间，归并排序的空间复杂度是O(n)

归并排序性能与记录的初始排列无关。无论是否有序，每趟都要逐个两子序列相互合并，一定要log2n趟

每趟排序不能够确定一个元素的最终排序位置，因为如果最后一个子序列包含最小元素，在最后一趟排序时要插入到最前位置，导致所有元素都要移动

6. 代码实现

可选择递归或非递归实现

//归并排序
void merge(string *a,string *b,int start,int mid,int left)
{int i=start,k=start,j=mid+1;while(i!=mid+1&&j!=left+1){if(a[i]>=a[j])b[k++]=a[i++];elseb[k++]=a[j++];}while(i!=mid+1)b[k++]=a[i++];while(j!=left+1)b[k++]=a[j++];for(i=start;i<=left;i++)a[i]=b[i];
}void merge_sort(string *a,string *b,int start,int end)  //递归实现归并排序
{if(start<end){int mid=start+(end-start)/2;merge_sort(a,b,start,mid);merge_sort(a,b,mid+1, end);merge(a,b,start,mid,end);}
}void merge_sort(string *a,string *b)  //非递归实现归并排序
{int right,left,mid;for(int i=1;i<l;i=2*i){for(left=0;left<l-1;left+=2*i){mid=left+i-1;if(mid>=l-1)break;right=left+2*i-1;if(right>=l)right=l-1;merge(a,b,left,mid,right);}}
}

基数排序

1. 基数排序：通过“分配”和“收集”若干次操作，对单逻辑关键字进行排序的一种方法。

2. 链式基数排序的算法设计：

基于最低位优先法思想

用链表作存储结构的基数排序

以十进制为例

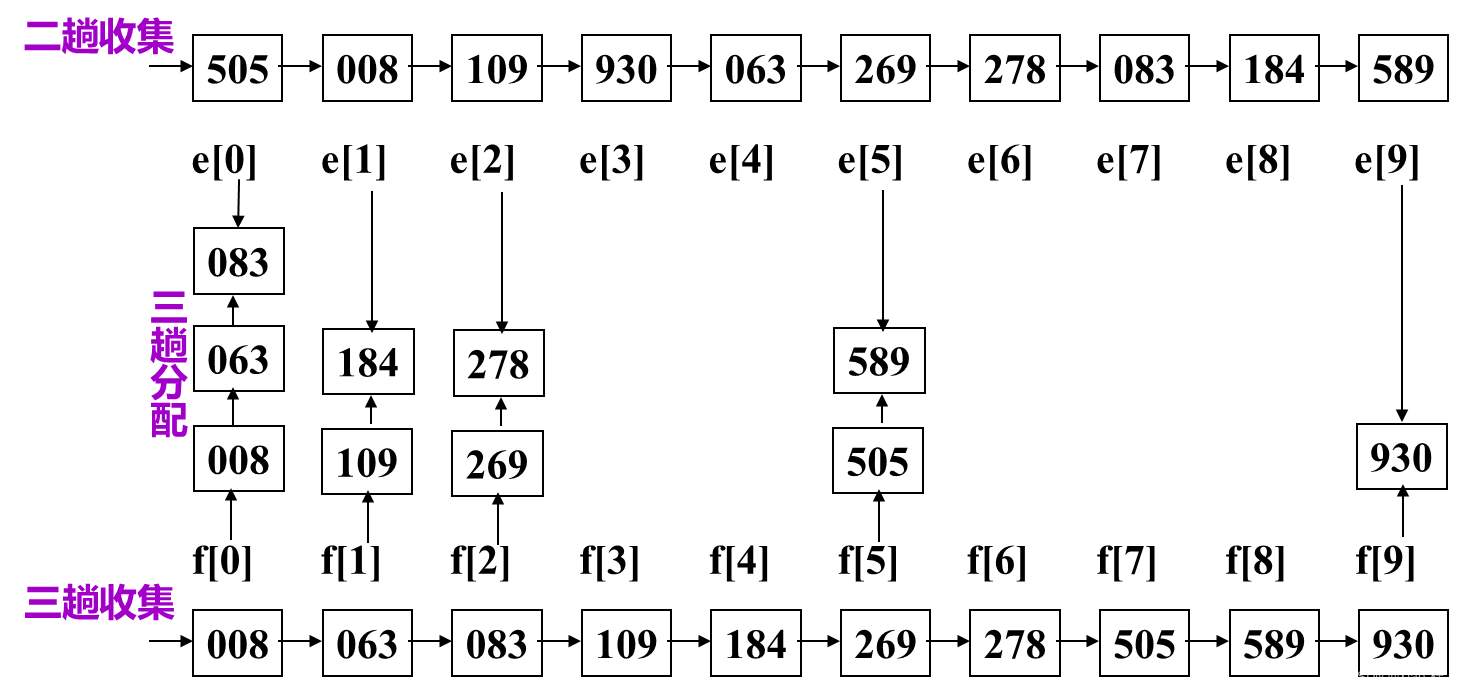
①.设置10个队列，f[i]和e[i]分别为第i个队列的头指针和尾指针

②.第i趟分配：根据第i位关键字的值，改变记录的指针，将链表中记录按次序分配至10个链队列中（采用队尾插入法）；每个队列中记录关键字的第i位关键字相同

③.第i趟收集：改变所有非空队列的队尾记录的指针域，令其指向下一个非空队列的队头记录，重新将10个队列链成一个链表

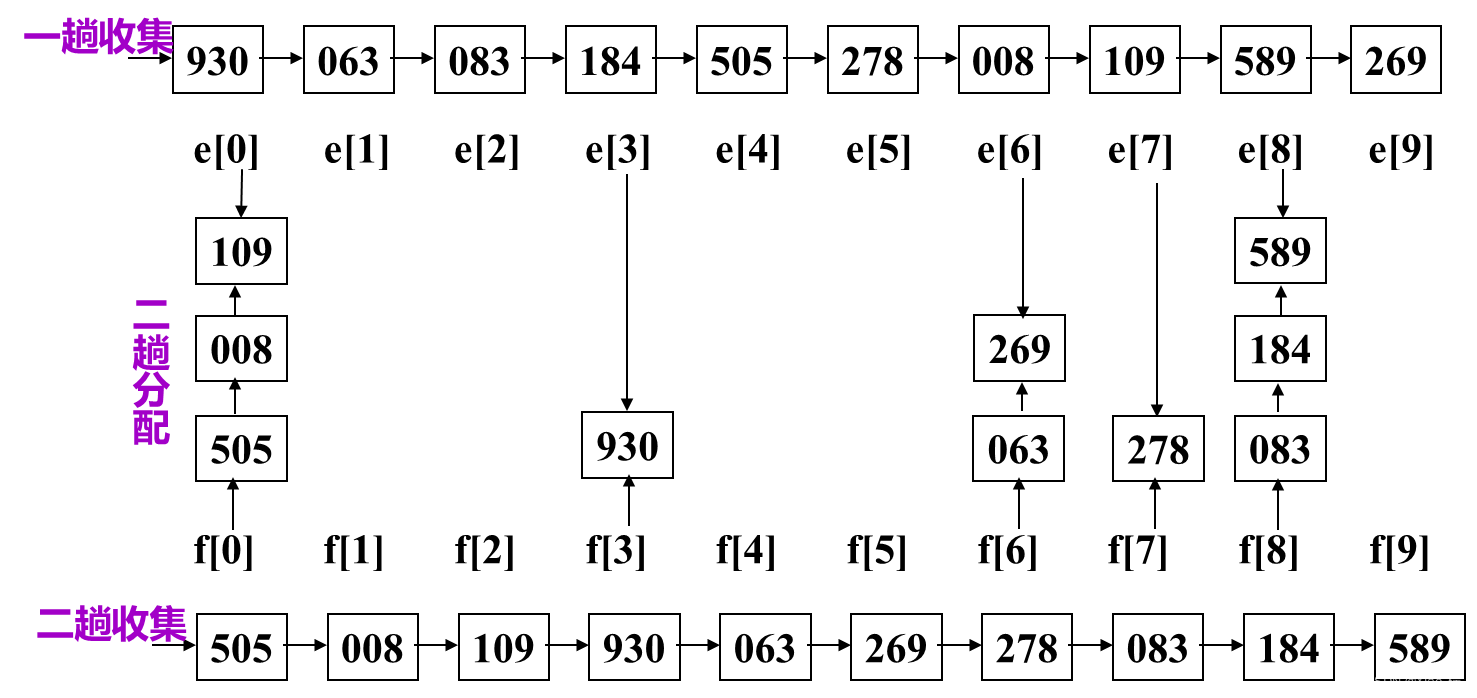
3. 链式基数排序的算法分析

若每个关键字有 d 位,关键字的基数为radix

需要重复执行d 趟“分配”与“收集”

每趟对 n 个对象进行“分配”，对radix个队列进行“收集”

时间复杂度为O(d(n+radix))

一般情况下radix表示k进制，是一个很小的值

所以时间复杂度为O(dn)，其中n是记录总数，d是关键字长度d位

是一种稳定的排序方法

4. 代码实现

// 基数排序的搜索函数
int radixSearch(vector<int>& arr, int target) {// 找到数组中的最大值int maxVal = *max_element(arr.begin(), arr.end());// 对每个位数进行基数排序for (int exp = 1; maxVal / exp > 0; exp *= 10) {vector<int> count(10, 0);  // 10个数字的计数数组// 统计每个数字的出现次数for (int i = 0; i < arr.size(); i++) {count[(arr[i] / exp) % 10]++;}// 计算累计出现次数for (int i = 1; i < 10; i++) {count[i] += count[i - 1];}// 构建排序后的数组std::vector<int> sortedArr(arr.size());for (int i = arr.size() - 1; i >= 0; i--) {sortedArr[count[(arr[i] / exp) % 10] - 1] = arr[i];count[(arr[i] / exp) % 10]--;}// 更新原始数组arr = sortedArr;}// 在排序后的数组中进行二分查找int left = 0;int right = arr.size() - 1;while (left <= right) {int mid = left + (right - left) / 2;if (arr[mid] == target) {return mid;} else if (arr[mid] < target) {left = mid + 1;} else {right = mid - 1;}}// 如果未找到目标值，返回-1return -1;
}