题目:https://leetcode.cn/problems/falling-squares/description/
在二维平面上的 x 轴上,放置着一些方块。
给你一个二维整数数组 positions ,其中 positions[i] = [lefti, sideLengthi] 表示:第 i 个方块边长为 sideLengthi ,其左侧边与 x 轴上坐标点 lefti 对齐。
每个方块都从一个比目前所有的落地方块更高的高度掉落而下。方块沿 y 轴负方向下落,直到着陆到 另一个正方形的顶边 或者是 x 轴上 。一个方块仅仅是擦过另一个方块的左侧边或右侧边不算着陆。一旦着陆,它就会固定在原地,无法移动。
在每个方块掉落后,你必须记录目前所有已经落稳的 方块堆叠的最高高度 。
返回一个整数数组 ans ,其中 ans[i] 表示在第 i 块方块掉落后堆叠的最高高度。
示例 1:
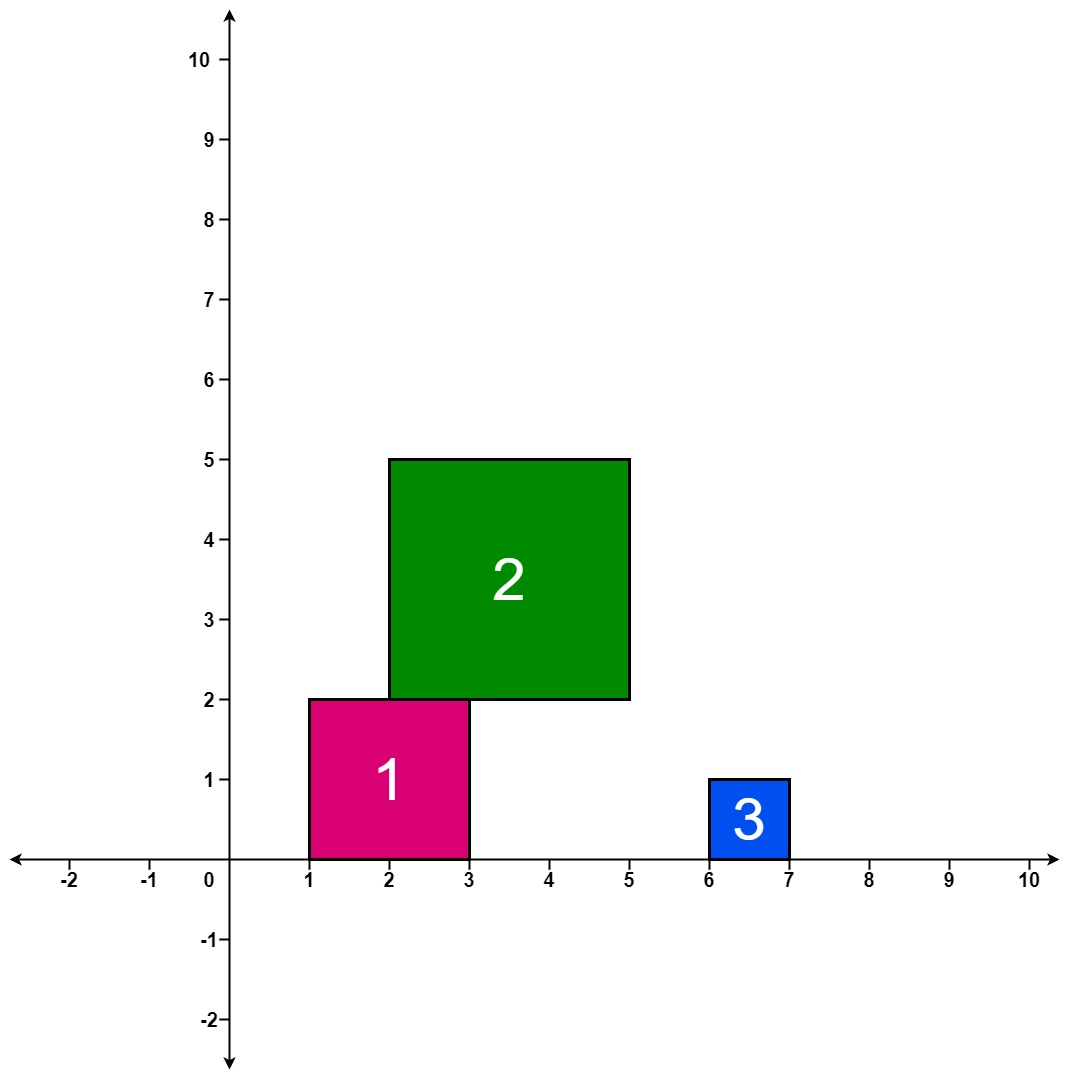
输入:positions = [[1,2],[2,3],[6,1]] 输出:[2,5,5] 解释: 第 1 个方块掉落后,最高的堆叠由方块 1 组成,堆叠的最高高度为 2 。 第 2 个方块掉落后,最高的堆叠由方块 1 和 2 组成,堆叠的最高高度为 5 。 第 3 个方块掉落后,最高的堆叠仍然由方块 1 和 2 组成,堆叠的最高高度为 5 。 因此,返回 [2, 5, 5] 作为答案。
示例 2:
输入:positions = [[100,100],[200,100]] 输出:[100,100] 解释: 第 1 个方块掉落后,最高的堆叠由方块 1 组成,堆叠的最高高度为 100 。 第 2 个方块掉落后,最高的堆叠可以由方块 1 组成也可以由方块 2 组成,堆叠的最高高度为 100 。 因此,返回 [100, 100] 作为答案。 注意,方块 2 擦过方块 1 的右侧边,但不会算作在方块 1 上着陆。
在算法40中,我们介绍了线段树以及使用线段树求累加和的案例。他们使用的都是一维数据,区间很好划分。而这一题是二维数组,二维数组中的每个一维数组第一个元素代表起始位置,第二个元素代表高度,思来想去,还是不知道如何去划分区间。
1. 之前的区间跟数据没关系,只是跟数据的位置有关系;而本题尝试以二维数组作为一个单元数据,没法划分;
2. 以X轴横坐标划分区间;假设数据量很大,而且数据范围也很大,比如{{1,10}, {10,1000000},{100000000, 100000000000000000}}; 这样的数组该如何去划分区间呢?貌似也走不通。
离散化技巧:
假设二维数组为 {
{300, 5000},{17, 67300},{4500, 5000万}
}
我们把这些坐标进行搜集并排序得到 17,300,4500,5000,67300,5000万; 按照线段树的思路给下标:
| 下标 :0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 忽略 | 17 | 300 | 4500 | 5000 | 67300 | 500万 |
如果按照这样的思路,我们就可以得到:
{300, 5000} = [2, 4] 区间
{17, 67300} = [1, 5] 区间
{4500, 5000万} = [3, 6] 区间
这样的技巧就叫做离散化技巧,确实很牛逼。我也是思考了很久,最终看了大神的解释才弄懂的。
本题分析;
假设二维数组中有一个数组 {1,3},1代表开始位置,3代表长度;得到开始、结束位置{1,4};
此时,又来一个数组 {4,2};代表4是开始位置,2是长度;得到开始、结束位置{4,6}
那么此时问题就来了,{1,4} 和 {4,6}存在相同的4;但是本题方块却可以正常紧挨着降落在一排;如果按照区间来划分算高度,4这个位置会出问题:
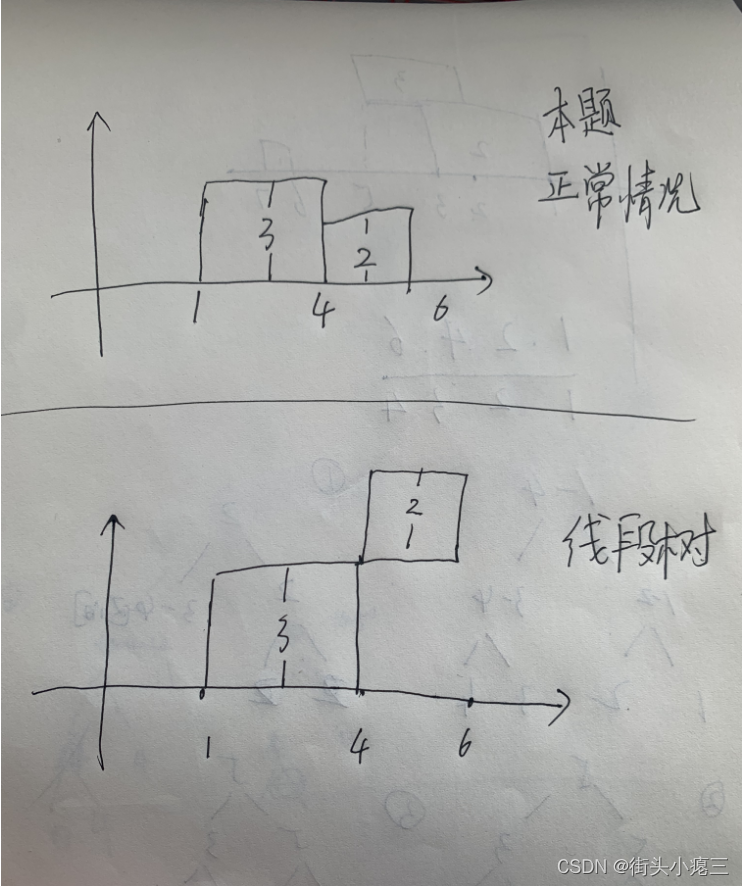
想要解决这样的问题,结束的位置坐标往左推一个就可以解决;
{1,4} 实际上代表的是 [1,4) 左闭右开; 给转换成 [1,3]
{4,6}实际上代表的是 [4,6) 左闭右开;给转换成 [4,5]
本题中的坐标都只能是整数,这是隐藏信息;因此,以上的转换是正确的。
区间的确定:
本题中,区间是根这些坐标有关系的;利用离散化技巧以及上方关于区间的分析可得;

我们以本题中给定的图片进行分析
第一个数是[1,3),我们得到[1,2]
第二个数是[2,5), 我们得到[2,4]
第三个数是[6,7), 我们得到[6,6]
无重复收集这些坐标信息,得到 {1,2,4,6},分别给个下标
| 下标0 | 1 | 2 | 3 | 4 |
| 忽略 | 1 | 2 | 4 | 6 |
这样,我们就知道了第一个方块在 1-2区间;第二个方块在 2-3区间;第三个方块在4区间;
本题是算最大高度的,因此无需原始数组;max数组全部为0即可;

当第一个方块{1,3}落下的时候,{1,3} 对应 1-2区间,也就是跟节点的左子树;那么左子树的高度就为 3; 跟节点取左、右子节点的最大值;
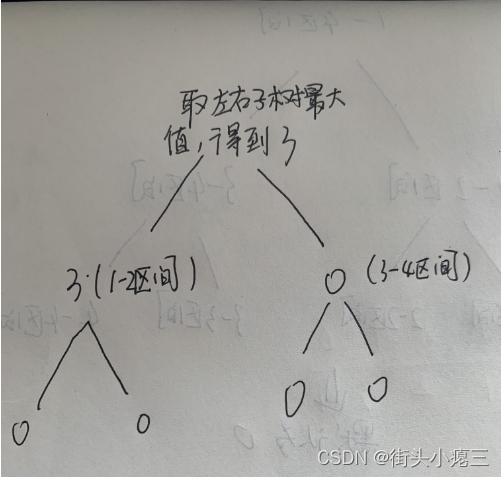
第二个方块{2,5}落下,{2,5}对应 2-3区间;此时,1-2区间的3下方到左、右子节点;
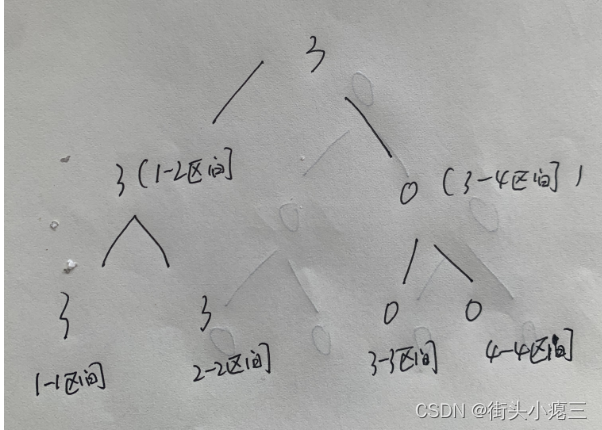
获取到2-3区间的最大值;目测是3;那么此时第二块方块落下以后,2-3区间的最大值就为 3+2 = 5;根节点取左、右子树最大值,也为5;

第三个方块{6,7}对应4区间;那么4区间高度就为1; 取值结果没有变化

目测整个线段树的最大高度会一直汇总到树的顶部,那么只要获取树的顶部数据,就可以获取到最大值了;
package code04.线段树_02;import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.TreeSet;/*** 力扣 699题 :掉落的方块* https://leetcode.cn/problems/falling-squares/description/*/
public class Code02_FallingSquares {class SegmentTree {int[] max;int[] lazy;boolean[] update;public SegmentTree(int size) {max = new int[size * 4];lazy = new int[size * 4];update = new boolean[size * 4];}//统计index节点,从左、右节点中选取较大的public void count(int index) {max[index] = Math.max(max[index * 2], max[index * 2 + 1]);}public void pushDown(int curIndex){//判断curIndex是否有懒数据没更新到子节点if (lazy[curIndex] != 0) {//左、右子区间加上懒更新的数据max[curIndex * 2] = lazy[curIndex];max[curIndex * 2 + 1] = lazy[curIndex];//左、右子树区间记录懒数据lazy[curIndex * 2] = lazy[curIndex];lazy[curIndex * 2 + 1] = lazy[curIndex];//原curIndex数据已经下放到子区间了,此处需要重置为0lazy[curIndex] = 0;}}public void add(int left, int right, int curIndex, int start, int end, int value){if (start <= left && end >= right) {//默认max中全部为高度全部为0. 那么下降一个方块,高度就选取大的加上下架的方块高度 valuemax[curIndex] = value;lazy[curIndex] = value;return;}int mid = (left + right)/2;//如果当前节点curIndex之前有懒的数据,那么把curIndex之前的懒//数据下放到子节点区间pushDown(curIndex);if (start <= mid) {add(left, mid, curIndex * 2, start, end, value);}if (end > mid) {add(mid + 1, right, curIndex * 2 + 1, start, end, value);}//重新汇总curIndex节点的最大值count(curIndex);}public int query(int left, int right, int curIndex, int start, int end){if (start <= left && end >= right) {return max[curIndex];}int max = 0;int mid = (left + right) / 2;pushDown(curIndex);if (start <= mid) {int ans = query(left, mid, curIndex * 2, start, end);max = Math.max(ans, max);}if (end > mid) {int ans = query(mid + 1, right, curIndex * 2 + 1, start, end);max = Math.max(ans, max);}return max;}public int getTreeMaxHeight(){return max[1];}}public HashMap<Integer, Integer> index(int[][] positions){TreeSet<Integer> pos = new TreeSet<>();//离散化过程,统计开始、结束区间的坐标。//不管数组长度为多少,最终都是落在这些区间中的for (int[] arr : positions) {pos.add(arr[0]);pos.add(arr[0] + arr[1] - 1);}int index = 1;HashMap<Integer, Integer> map = new HashMap<>();//给每个下标编个index,从1开始; 模拟原始线段树的原始数组中给每个元素添加下标的逻辑/* for(Iterator iterator = pos.iterator(); iterator.hasNext();) {int key = (int) iterator.next();map.put(key, index++);}*/for (Integer key : pos) {map.put(key, index++);}return map;}public List<Integer> fallingSquares(int[][] positions){//获取到了X轴上对应的下标HashMap<Integer, Integer> map = index(positions);int size = map.size();SegmentTree segmentTree = new SegmentTree(size);int left = 1;int right = size;int curIndex = 1;List<Integer> list = new ArrayList<>();for (int i = 0; i < positions.length; i++) {//任务开始下标int startIndex = map.get(positions[i][0]);//修改的值int value = positions[i][1];//任务结束下标; 此下标代表 [1,4) 替换成 [1,3]int endIndex = map.get(positions[i][0] + value - 1);//这个地方比较有意思,假如3-4区域高度max为5.//再降落一块高度为3的石头在1-3区间。不考虑重力因素//1-3的高度应该为 5 + 3 = 8; 哪怕之前1-2区域高度为0int ans = segmentTree.query(left, right, curIndex, startIndex, endIndex);int height = ans + value;//降落一块方块segmentTree.add(left, right, curIndex, startIndex, endIndex, height);//全区间查找最大值System.out.println(segmentTree.getTreeMaxHeight());list.add(segmentTree.getTreeMaxHeight());}return list;}public static void main(String[] args) {Code02_FallingSquares ss = new Code02_FallingSquares();//输出2 5 5int[][] positions = {{1,2},{2,3},{6,1}};ss.fallingSquares(positions);
/*int[][] positions2 = {{100,100},{200,100}};ss.fallingSquares(positions2);int[][] positions3 = {{9,7},{1,9},{3,1}};ss.fallingSquares(positions3);int[][] positions4 = {{6,4},{2,7},{6,9}};ss.fallingSquares(positions4);*/}
}
一顿操作猛如虎,结果测试发现胜率不到10%;
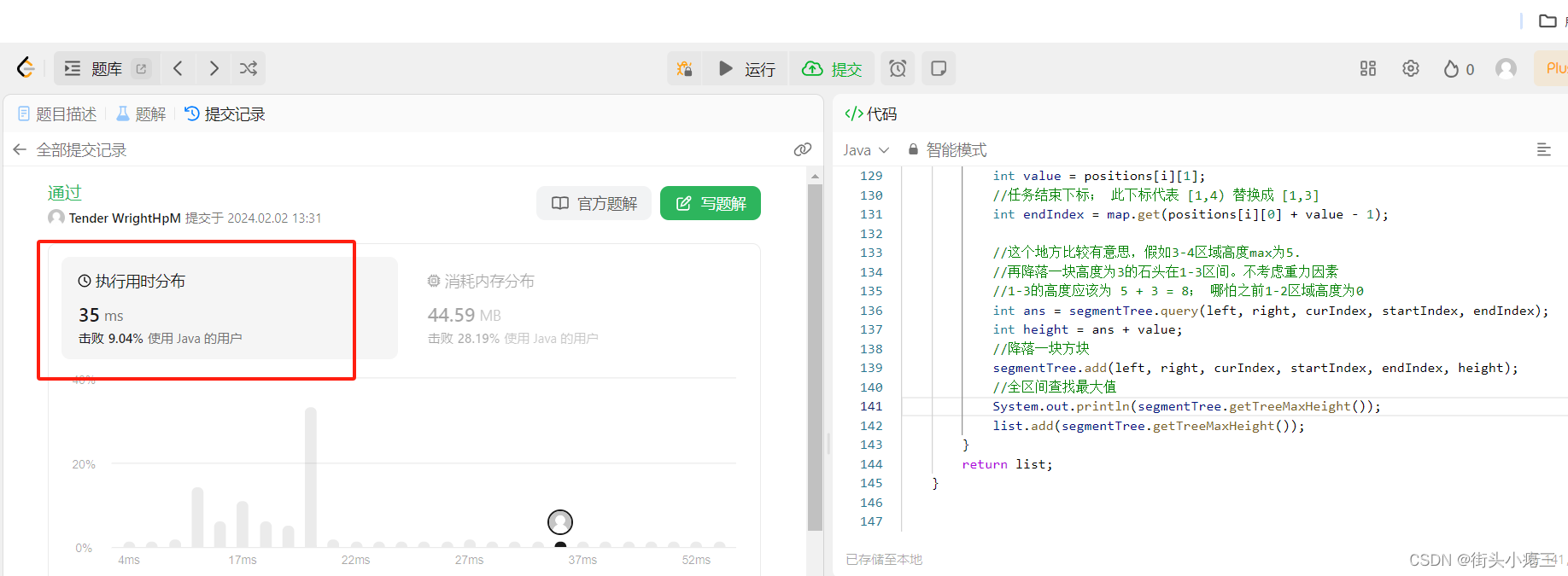
查了好久代码,没有发现什么结构上的问题。最终只注释掉了一行:
System.out.println(segmentTree.getTreeMaxHeight());
再测试发现, 96%的胜率:
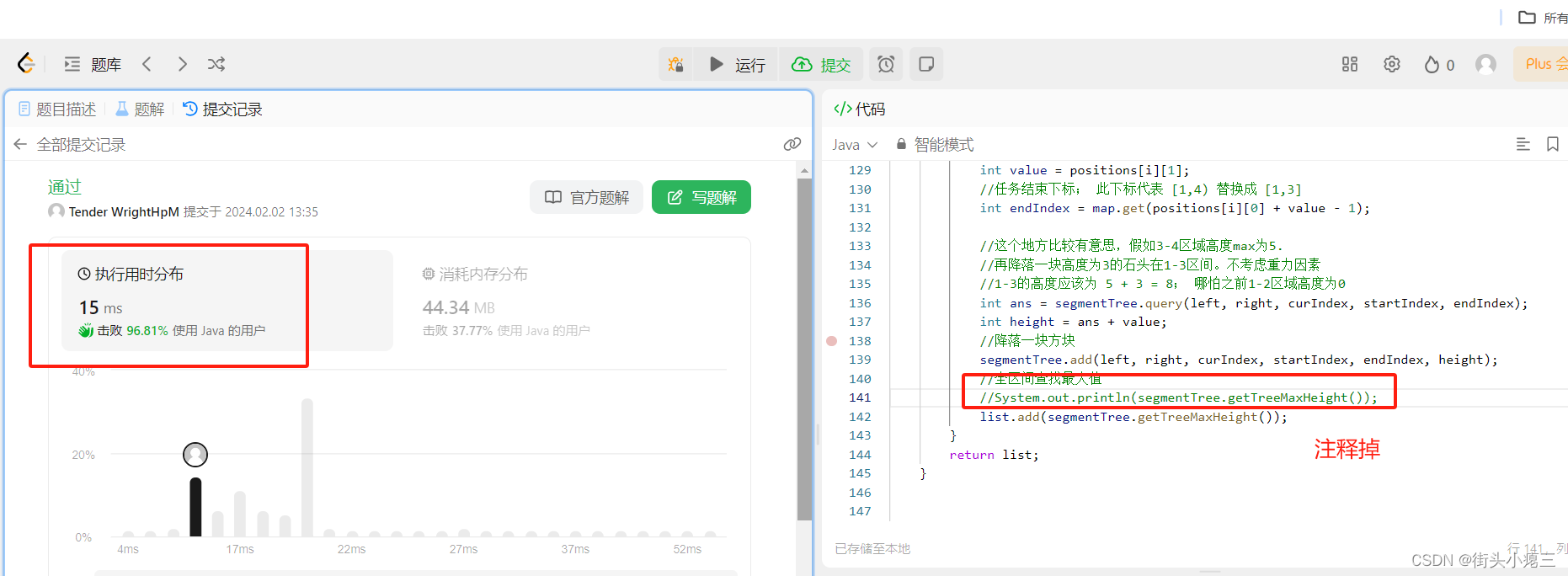

![[.NET] 查询当前已安装所有 Win32 与 UWP 应用](https://img-blog.csdnimg.cn/img_convert/3f7e7f9cf254a8d7e00e123e6d81fd86.png)