数组：一组地址连续的空间。

数组是定长线性表在维数上的扩展，即，线性表中的元素又是一个线性表。

一、数组

数组的特点：

数组数目固定，一旦定义了数组结构，不再有元素个数的增减变化。因此，数组一般不做插入、删除操作，适合用于顺序存储结构。

1-1、一维数组

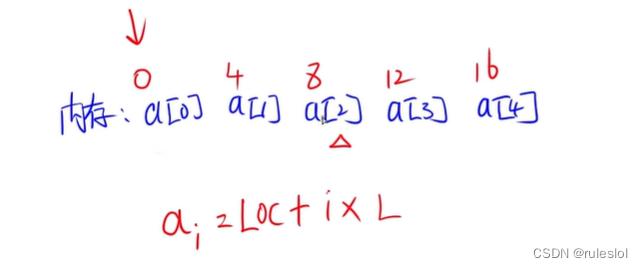
• L：元素大小
• LOC：元素首地址

数组从0开始：

ai的地址 = LOC + (i)*L

ai的前面有i个元素

数组从1开始：

ai的地址 = LOC + (i-1)*L

ai的前面有i-1个元素

1-2、二维数组

a[N][M]：N行、M列

L：元素大小

在内存中存储如下：

1、a[N][M]按行优先存储

求a[i][j]的首地址：

① 数组下标从0开始：a[0][0]

先求出 a[i][j]前面有多少行：i行

再求出 a[i][j]前面有多少列：j列

a[i][j] = LOC + (i * M + j) * L

②数组下标从1开始：a[1][1]

a[i][j] = LOC + [(i-1) * M + (j-1)] * L

2、a[N][M]按列优先存储

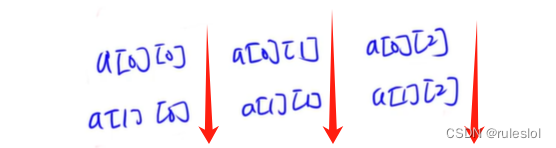
 求a[i][j]的首地址：

① 数组下标从0开始：a[0][0]

先求出 a[i][j]前面有多少列：j列

再求出 a[i][j]前面有多少行：i行

a[i][j] = LOC + (j * N + i) * L

① 数组下标从1开始：a[1][1]

a[i][j] = LOC + [(j-1) * M + (i-1)] * L

3、特殊情况a[N][N]

对于N行N列数组

求a[i][i]时，不管是按行存储还是按列存储，其存储的首地址和该元素前面的元素个数，都是相同的。

示例：

1-3、真题

真题1：

真题2：

真题3：

二、矩阵

一个二维数组就是一个矩阵。 

矩阵的存储，即，将一个二维数组的元素，压缩存储在一个一维数组中。

矩阵的压缩存储：

多个值相同的元素，分配一个存储单元；0不分配存储单元。

2-1、特殊矩阵

值相同的元素、0元素在矩阵中有一定的规律——特殊矩阵

2-1-1、对称矩阵

Aij = Aji

示例：

对称矩阵的存储：只存储主对角线的元素 + 下三角区（上三角区）的元素

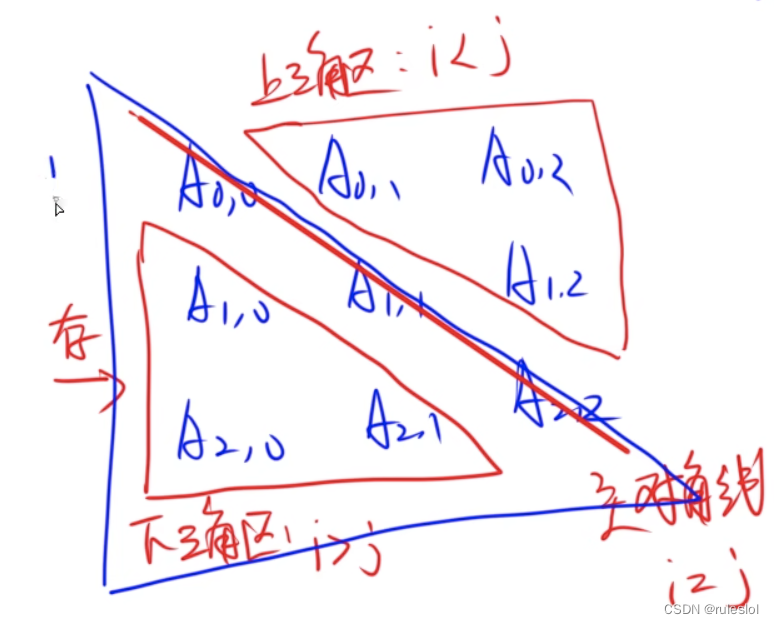
存储的元素个数：(1+n)n/2

对称矩阵按行优先存储：

期望：通过A22——>a6

求：Aij

1、数组下表从0开始

①前i-1行有多少个元素？i*(1+i)/2

②第i行，前j-1列有几个元素？j

③再加上自己

Aij = i*(1+i)/2 + j + 1（当i >= j）

Aij = j*(1+j)/2 + i + 1（当i < j）

2、下标从1开始

 

2-1-2、三对角矩阵 

三对角矩阵的存储：

只存储对角线上的非0元素。

期望：通过A33——>a10

求：Aij

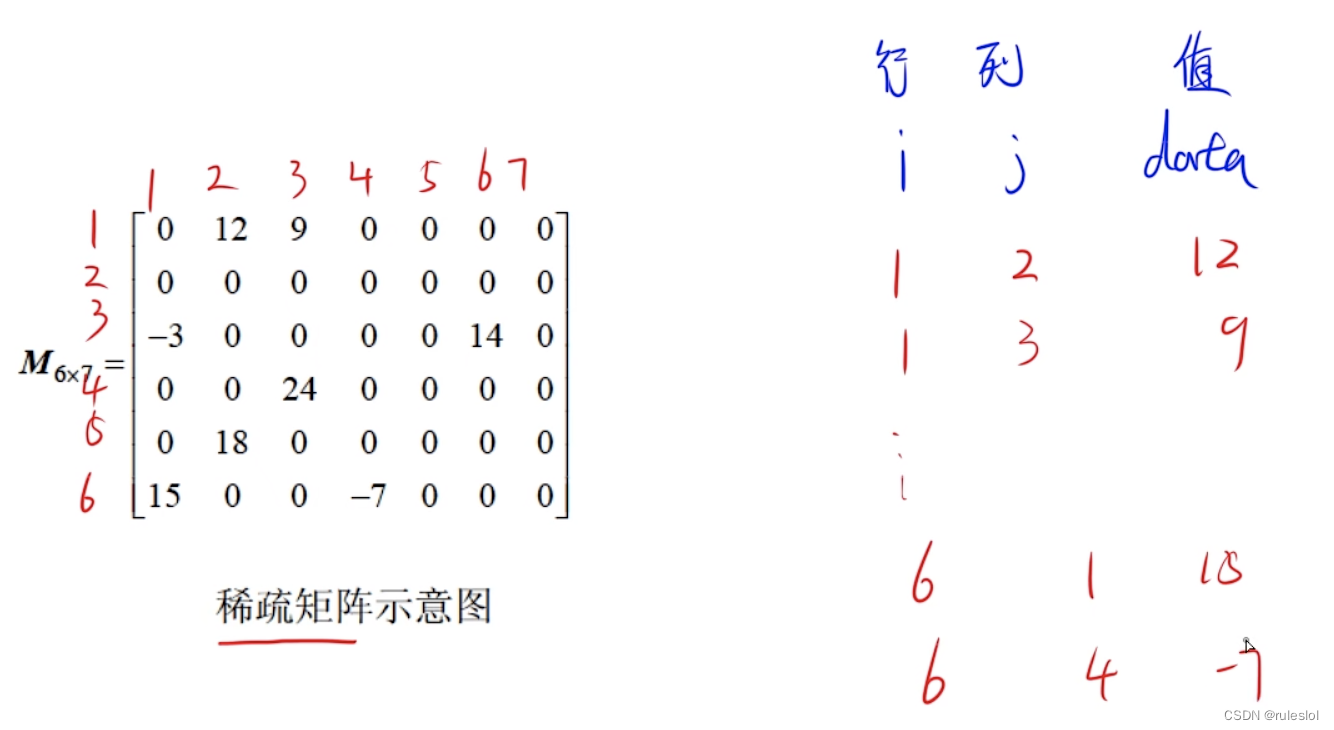
2-2、稀疏矩阵

矩阵中，非0元素的个数远少于0元素的个数，非0元素分布没有规律。

示例：

稀疏矩阵的压缩存储：

• 三元组顺序表（顺序存储）
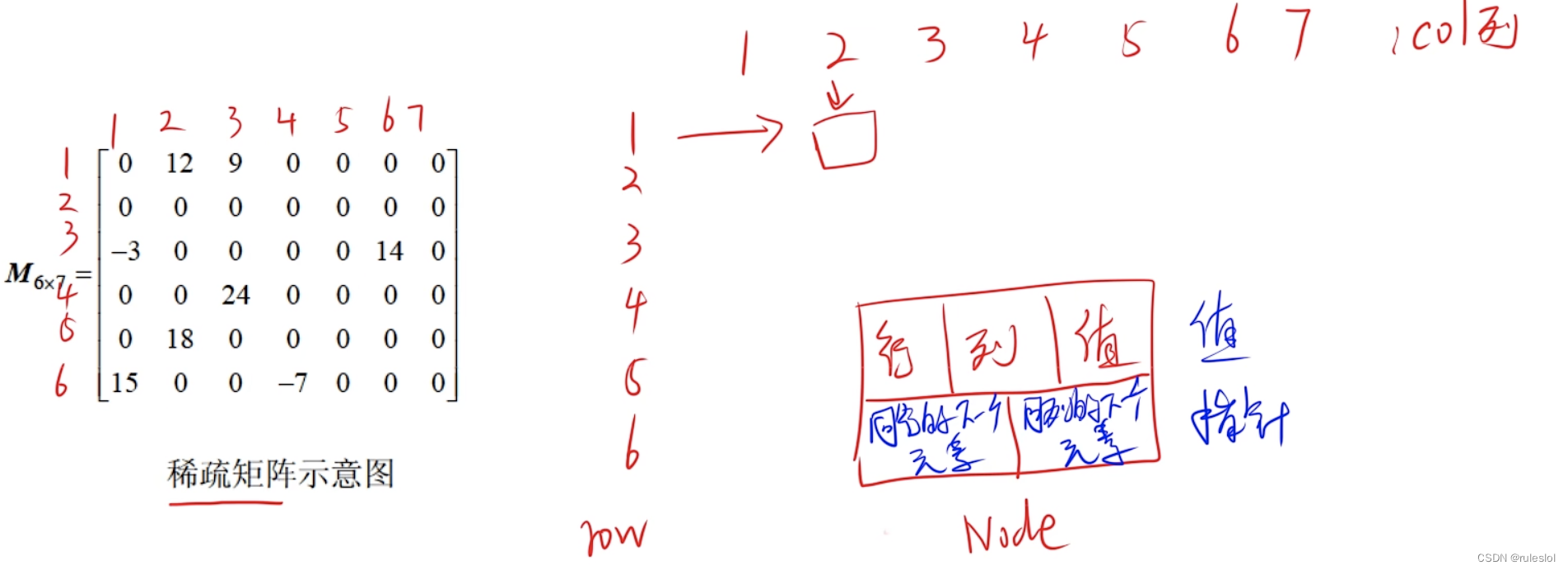
• 十字链表（链式存储）

2-2-3、三元组顺序表

2-2-4、十字链表

2-3、真题

真题1：

真题2：

真题3：

真题4：

真题5：

真题6：

 真题7：